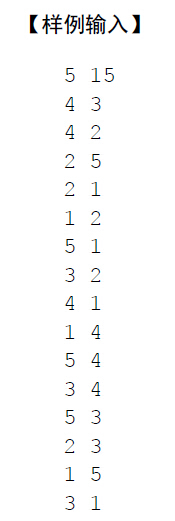[清华集训2015 Day1]主旋律-[状压dp+容斥]

 

Description

Solution

f[i]表示状态i所代表的点构成的强连通图方案数。

g[i]表示状态i所代表的的点形成奇数个强连通图的方案数-偶数个强连通图的方案数。

g是用来容斥的。

先用f更新g。枚举状态i的编号最小点k所在连通块大小i-j，$g[i]=-sum _{jsubset i}f[i-j]*g[j]$(此处g中不更新强连通图个数为1的。

设点集i中有sum条边，则：

$f[i]=2^{sum}-sum _{jsubset i}2^{sum-w[j]}*g[j]$。其中w[j]是i射向j的边数，这些边被钦定不能选。

最后记得用f[i]更新g[i]。

Code

 

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
using namespace std;
typedef long long ll;
const int mod=1e9+7;
int n,m,x,y;
int in[40010],out[40010];
int num[40010],sum[40010];
ll f[40010],g[40010],bin[40010],w[40010];
void calw(int s,int c)
{
    if (!c) return;
    calw(s,(c-1)&s);
    w[c]=w[c^(c&-c)]+num[in[c&-c]&s];
}
int main()
{
    scanf("%d%d",&n,&m);
    bin[0]=1;for (int i=1;i<=m;i++) bin[i]=(bin[i-1]<<1)%mod;  
    for (int i=1;i<=m;i++)
    {
        scanf("%d%d",&x,&y);x--;y--;
        in[bin[y]]|=bin[x];
        out[bin[x]]|=bin[y];
    }
    for (int i=1;i<bin[n];i++) for (int j=0;j<n;j++) 
    if (i&bin[j]) num[i]++;
     
    for (int i=1;i<bin[n];i++)
    {
        int lowbit=i&-i,s=i^lowbit;
        for (int j=s;j;j=s&(j-1)) g[i]=(g[i]-f[j^i]*g[j]%mod)%mod;
         
        sum[i]=sum[s]+num[in[lowbit]&s]+num[out[lowbit]&s];
        f[i]=bin[sum[i]];
        calw(i,i);
         
        for (int j=i;j;j=i&(j-1))
        {
            f[i]=(f[i]-bin[sum[i]-w[j]]*g[j]%mod+mod)%mod;
        } 
        g[i]+=f[i];if (g[i]>=mod) g[i]%=mod;
    }
    cout<<f[bin[n]-1];
     
}