CF504E Misha and LCP on Tree [*3000]
Solution
垃圾题。
考虑 LCP 问题的经典解法,二分一个前缀,判定这个前缀能否成为 LCP。
判定前缀考虑 Hash,需要预处理出每个点从根到它,从它到根的哈希值。
然后我们发现,每次二分之后需要找终点,这个得 \(O(1)\) 做,使用长链剖分求 k 级祖先就可以了。
然后你就判判判,然后你就被迫要卡常,总之就很离谱。
时间复杂度 \(O(m\log n)\),其中 \(\log n\) 是倍增 LCA。
然后用 ST 表 LCA 可以做到 \(O(n\log n+m)\),不过我没写。
Code
const int mod=998244353;
const int base=13331;
const int N=6e5;
int Up[N+10],Down[N+10];
int n,q,h[N+10],ju[N+10][20];
vector<int> G[N+10];
int md[N+10],dep[N+10],hson[N+10],top[N+10];
int po[N+10],inv[N+10];
int pos[N+10],dfn[N+10],jp[N+10],dc;
char ch[N+10];
int fpow(int x,int y) {
int ret=1;
for(;y;y>>=1) {
if(y&1) ret=1ll*ret*x%mod;
x=1ll*x*x%mod;
}
return ret;
}
void ad(int u) {
Down[u]=(1ll*Down[ju[u][0]]*base+ch[u])%mod;
Up[u]=(Up[ju[u][0]]+1ll*po[dep[ju[u][0]]]*ch[u])%mod;
dep[u]=dep[ju[u][0]]+1;
for(int i=1;i<=19;i++) ju[u][i]=ju[ju[u][i-1]][i-1];
for(auto v:G[u]) {
if(v==ju[u][0]) continue;
ju[v][0]=u;ad(v);
if(md[v]+1>md[u]) md[u]=md[hson[u]=v]+1;
}
}
void dfs(int u) {
if(hson[ju[u][0]]==u) top[u]=top[ju[u][0]];
else top[u]=u;
pos[dfn[u]=++dc]=u;
if(hson[u]) dfs(hson[u]);
for(auto v:G[u]) {
if(v==ju[u][0]||v==hson[u]) continue;
dfs(v);
jp[dfn[v]]=u;
for(int i=1;i<=md[v];i++)
jp[dfn[v]+i]=ju[jp[dfn[v]+i-1]][0];
}
}
int LCA(int u,int v) {
if(u==v) return u;
if(dep[u]<dep[v]) swap(u,v);
for(int i=19;i>=0;i--)
if(dep[ju[u][i]]>=dep[v])
u=ju[u][i];
if(u==v) return u;
for(int i=19;i>=0;i--)
if(ju[u][i]!=ju[v][i])
u=ju[u][i],v=ju[v][i];
return ju[u][0];
}
int calc(int u,int k) {
return jp[dfn[u]+k-1];
}
int ask(int u,int k) {
if(!k) return u;
u=ju[u][h[k]];
k-=1<<h[k];
if(dep[u]-dep[top[u]]<k)
return calc(top[u],-dep[u]+k+dep[top[u]]);
else return pos[dfn[u]-k];
}
void init() {
ad(1);
// up[1].pb(1);
// for(int i=1;i<=md[1];i++) up[1].pb(ju[up[1].back()][0]);
dfs(1);
}
int get(int a,int b,int p) {
if(p==-1) p=b;
int H1=1ll*(Up[a]-Up[ju[p][0]]+mod)*inv[dep[p]-1]%mod;
int H2=(Down[b]-1ll*Down[p]*po[dep[b]-dep[p]]%mod+mod)%mod;
return (1ll*H1*po[dep[b]-dep[p]]+H2)%mod;
}
int query(int a,int b,int c,int d) {
int lca1=LCA(a,b),lca2=LCA(c,d);
int dis1=dep[a]+dep[b]-2*dep[lca1]+1,
dis2=dep[c]+dep[d]-2*dep[lca2]+1;
int l=1,r=min(dis1,dis2);
while(l<=r) {
int mid=(l+r)>>1;
// printf("[%d,%d] is %d\n",l,r,mid);
int h1=0,h2=0;
if(dep[a]-dep[lca1]+1>=mid) h1=get(a,ask(a,mid-1),-1);
else h1=get(a,ask(b,dis1-mid),lca1);
if(dep[c]-dep[lca2]+1>=mid) h2=get(c,ask(c,mid-1),-1);
else h2=get(c,ask(d,dis2-mid),lca2);
// printf("%d %d\n",h1,h2);
if(h1==h2) l=mid+1;
else r=mid-1;
}
return l-1;
}
int main() {
n=read();
gs(ch+1);
po[0]=inv[0]=1;
po[1]=base,inv[1]=fpow(base,mod-2);
for(int i=2,x,y;i<=n;i++) {
x=read(),y=read();
G[x].pb(y),G[y].pb(x);
po[i]=1ll*po[i-1]*base%mod,
h[i]=h[i/2]+1,
inv[i]=1ll*inv[i-1]*inv[1]%mod;
}
init();
q=read();
while(q--) {
int a,b,c,d;
a=read(),b=read(),c=read(),d=read();
write(query(a,b,c,d)),pc('\n');
}
return fl;
}
ABC225F String Cards [*2612]
有 \(n\) 个字符串 \(S_i\),从中选出 \(k\) 个字符串,按任意顺序拼接,求最后字典序最小的字符串。
\(1\le k\le n\le 50\),\(1\le |S_i|\le 50\)。
Solution
经典问题的改版,但其实很出乎意料。
官方题解 hack 了若干种错误的 DP 与贪心,建议可以自己去看,这里只阐述解法。
先对 \(S_i\) 排序,保证对于相邻的 \(i,j\),必然有 \(S_i+S_j<S_j+S_i\)。
考虑 DP,设 \(f_{i,j}\) 表示 \([i,n]\) 中,选了 \(j\) 个之后的最小字典序方案。
有转移:\(f_{i,j}=\min(f_{i+1,j},S_i+f_{i+1,j-1})\)。
暴力 DP,时间复杂度 \(O(n^2\sum|S_i|)\)。
Code
int n,k;
string S[60],f[60][60];
bool cmp(string a,string b) {
return a+b<b+a;
}
int main() {
scanf("%d %d",&n,&k);
for(int i=1;i<=n;i++) cin>>S[i];
sort(S+1,S+n+1,cmp);
// for(int i=1;i<=n;i++) cout<<S[i]<<endl;
for(int i=n;i>=1;i--)
for(int j=1;j<=min(n-i+1,k);j++) {
f[i][j]=f[i+1][j];
if(f[i][j]==""||f[i][j]>S[i]+f[i+1][j-1]) f[i][j]=S[i]+f[i+1][j-1];
// printf("%d,%d\n",i,j);
// cout<<f[i][j]<<endl;
}
cout<<f[1][k]<<endl;
}
ABC225G X [*2566]
给定一个 \(h\times w\) 的二维数组,现在高桥要在上面做标记,标记是 \(\times\),画一条线的费用是 \(C\),价值是做标记的数总和减去划线的费用,注意连在一起的线可以一起画,求最大价值。
\(1\le h,w\le 100\),\(1\le C,a_{i,j}\le 10^9\)。
Solution
考虑建模,我们发现这里的代价是时加时减的,不好处理,考虑换个思路。
考虑全部归约为减,先求出所有 \(a\) 的权值和,那么问题就变成了,求出一些位置,他们不被标记,且权值和加划线的和最小。
那么可以直接网络流建模,比如说,规定一个位置 \((i,j)\),按情况讨论:
- 由源点到 \((i,j)\) 连一条容量为 \(a_{i,j}\) 的边。
- 若 \((i-1,j-1)\) 存在,向 \((i-1,j-1)\) 连一条容量为 \(C\) 的边,否则向汇点连一条这样的边。
- 若 \((i-1,j+1)\) 存在,与上述同理。
直接跑最小割。
Code
使用了 AtCoder Library。
const int N=100;
int n,m,C;
int a[N+10][N+10];
int bh(int x,int y) {
return x*m+y;
}
int main() {
scanf("%d %d %d",&n,&m,&C);
mf_graph<ll> G(n*m+2);
ll ans=0;
for(int i=0;i<n;i++)
for(int j=0;j<m;j++)
scanf("%d",&a[i][j]),ans+=a[i][j];
for(int i=0;i<n;i++)
for(int j=0;j<m;j++)
G.add_edge(n*m,bh(i,j),a[i][j]);
for(int i=0;i<n;i++)
for(int j=0;j<m;j++) {
if(i>0&&j>0) G.add_edge(bh(i,j),bh(i-1,j-1),C);
else G.add_edge(bh(i,j),n*m+1,C);
if(i>0&&j<m-1) G.add_edge(bh(i,j),bh(i-1,j+1),C);
else G.add_edge(bh(i,j),n*m+1,C);
}
printf("%lld\n",ans-G.flow(n*m,n*m+1));
}
AGC020C Median Sum [*2259]
Solution
直接求非空子集和的方法不可取,暴力做是 \(O(2^n)\)。
但不同子集和的总数很小,只有 \(\sum A_i\) 个,所以考虑背包。
暴力背包的复杂度是 \(O(n\sum A_i)\),不稳,直接 bitset 一波,变成 \(O(\frac{n\sum A_i}{\omega})\)。
接下来考虑求解,不难发现,如果 \(x\) 可以被凑出,那么 \(\sum A_i-x\) 一定可以被凑出。
所以直接从 \(\frac{\sum A_i}{2}\) 开始扫起,第一个就是中位数。
那么时间复杂度 \(O(\frac{n\sum A_i}{\omega}+\sum A_i)\)。
Code
bitset<2000*2000+10> f;
int sum,n;
int main() {
scanf("%d",&n);
f[0]=1;
for(int i=1,x;i<=n;i++) {
scanf("%d",&x);
sum+=x,f|=(f<<x);
}
for(int i=(sum+1)/2;;i++)
if(f[i]) {
printf("%d\n",i);
return 0;
}
}
AGC020D Min Max Repetition [*3062]
Solution
设 \(m=\max\{A,B\}\),\(n=\min\{A,B\}\)
\(l\) 为段长。
构造 AA……ABAA……AB……AABB……BB……BABB……BA。
前半的位置 \(i\bmod (l+1)=0\) 放 \(B\),后半的位置 \((A+B-i+1)\bmod (l+1)=0\) 放 \(A\)。
找前后半分割点,先求 A 在前半被分的段数 \(x\)。
若 \(l=1\),\(x=A\) 或 \(0\),取决于 \(A,B\) 的大小。
考虑分成 \(x\) 段之后怎么处理,前半 B 已经放了 \(x-1\) 个,那么后半得放 \(res_B=B-x+1\) 个 B。
同时前半至少需要 \(l\times (x-1)+1\) 个 A,所以后半至多剩下 \(res_A=A-l\times (x-1)-1\) 个 A。
剩下的 A 把 B 进行了分段,所以 \(res_B\) 至多 \((res_A+1)\times l\) 个。
所以有:
因为字典序最小,所以 \(x\) 最大,所以:
所以后半部分大小为 \(res_B+\lceil\frac{res_B}{l}\rceil\) 个,也就可以求出断点,那么这题做完了。
时间复杂度 \(O(\sum D-C)\)。
Code
int a,b,c,d;
void solve() {
scanf("%d %d %d %d",&a,&b,&c,&d);
int n=min(a,b),m=max(a,b);
int l=(n==m)?1:(m-1)/(n+1)+1;
int x;
if(l!=1) x=max((ll)(1ll*a*l+1ll*l*l-b-1)/(1ll*l*l-1),1ll);
else x=(a>=b?a:0);
int hou=(b-x+1)+(b-x+1)/l;
int D=a+b-hou;
for(int i=c;i<=d;i++)
if(i<=D) {
if(i%(l+1)==0) putchar('B');
else putchar('A');
}
else {
if((a+b-i+1)%(l+1)==0) putchar('A');
else putchar('B');
}
puts("");
}
int main() {
int T;scanf("%d",&T);
while(T--) solve();
}
CF1491F Magnets [*2700]
Solution
如果找出一块有磁性的磁石,把这个磁石与其他的相比就可以求出所有没磁性的。
但其实,想要 \(\log\) 的找出某一块有磁性的磁石是不可能的,考虑求出第二块有磁性的磁石,如果我们从前往后找,比如现在在 \(i\),那么询问 \([1,i-1]\) 与 \(i\),如果有磁性就说明 \(i\) 是有磁性的磁石。
\(i\) 后面的每一块磁石的磁性可以直接用一次询问求出,而寻找第一块有磁性的磁石使用二分。
时间复杂度 \(O(n^2)\),询问次数 \(n+\log n\)。
Code
void solve() {
scanf("%d",&n);ans.clear();
for(int i=2;i<=n;i++) {
printf("? %d 1\n",i-1);
for(int j=1;j<i;j++) printf("%d ",j);
puts("");
printf("%d\n",i);
fflush(stdout);
int x;scanf("%d",&x);
if(x) {
for(int j=i+1;j<=n;j++) {
printf("? 1 1\n");
printf("%d\n",j);
printf("%d\n",i);
fflush(stdout);
int y;scanf("%d",&y);
if(!y) ans.pb(j);
}
int L=1,R=i-1,ss=0;
while(L<=R) {
int mid=(L+R)>>1;
printf("? %d 1\n",mid);
for(int j=1;j<=mid;j++) printf("%d ",j);
puts("");
printf("%d\n",i);
fflush(stdout);
int y;scanf("%d",&y);
if(y) R=mid-1,ss=mid;
else L=mid+1;
}
for(int j=1;j<i;j++)
if(j!=ss) ans.pb(j);
printf("! %d",(int)ans.size());
for(auto fuck:ans) printf(" %d",fuck);
puts("");
fflush(stdout);
return;
}
}
}
ABC044D/ARC060B Digit Sum [*2261]
Solution
先考虑特殊情况,如果 \(n<s\),直接无解,如果 \(n=s\),那么解一定是 \(n+1\)。
考虑剩下的情况,设答案为 \(b\),如果 \(b\le \sqrt{n}\),我们可以直接暴力求进制数。
而当 \(b>\sqrt{n}\) 的时候,发现这个时候的数一定只有两位,设这两位分别是 \(x,y\),那么 \(n=bx+y,s=x+y\),两式相减得 \(n-s=(b-1)x\),那么 \(x\) 必然是 \(n-s\) 的因数,直接暴力枚举 \(x\)。
时间复杂度 \(O(\sqrt{n}\log n)\),\(\log\) 的底数不定。
不知道为什么会有人算出 \(O(\sqrt{n})\)。
Code
ll calc(ll n,ll b) {
if(n==0) return 0;
return calc(n/b,b)+n%b;
}
ll s,n,ans=-1;
int main() {
scanf("%lld %lld",&n,&s);
if(n<s) {
puts("-1");
return 0;
}
if(n==s) {
printf("%lld\n",n+1);
return 0;
}
for(int b=2;1ll*b*b<=n;b++)
if(calc(n,b)==s) {
printf("%d\n",b);
return 0;
}
for(int x=1;1ll*x*x<=n-s;x++)
if((n-s)%x==0&&calc(n,(n-s)/x+1)==s) ans=(n-s)/x+1;
printf("%lld\n",ans);
}
CF958C3 Encryption (hard) [*2500]
Soltution
设 \(f_{i,j}\) 表示前 \(i\) 个,选了 \(j\) 段的最小价值。
直接暴力转移不可取,考虑研究性质。
设 \(a\) 的前缀和为 \(s\),因为有 \(f_{i,j}\equiv s_n\pmod{p}\),所以说,对于两个决策 \(x,y\),同时设 \(w_x=(s_i-s_x)\bmod p\) 有:\(f_{x,j-1}+w_x\equiv f_{y,j-1}+w_y\pmod{p}\)。
\(w_x\) 和 \(w_y\) 必然不超过 \(p\),假设 \(f_{x,j-1}<f_{y,j-1}\),那么 \(f_{x,j-1}+w_x\le f_{y,j-1}+w_y\)。
直接对每个 \(j\) 记录 \(f_{i,j}\) 最大的 \(i\),时间复杂度 \(O(nk)\)。
Code
const int N=5e5,M=100;
int n,K,p,a[N+10];
int f[N+10][M+10];
int g[M+10];
int main() {
scanf("%d %d %d",&n,&K,&p);
for(int i=1;i<=n;i++) scanf("%d",&a[i]),a[i]=(a[i-1]+a[i])%p;
memset(f,0x3f,sizeof f);
f[0][0]=0,g[0]=0;
for(int i=1;i<=n;i++) {
for(int j=1;j<=K;j++) chkmin(f[i][j],f[g[j-1]][j-1]+(a[i]-a[g[j-1]]+p)%p);
for(int j=1;j<=K;j++) if(f[g[j]][j]>f[i][j]) g[j]=i;
}
printf("%d\n",f[n][K]);
}
AGC025D Choosing Points [*2868]
给定 \(n,D_1,D_2\),要求构造一个在 \(2n\times 2n\) 的网格中选出 \(n^2\) 个点的方案, 使得任意两点间的距离不为 \(\sqrt{D_1}\) 或 \(\sqrt{D_2}\)。
Solution
解法:将两个距离为 \(D\) 的点连边,问题转化成取出这张图的一个独立集,可以证明连出的图是一张二分图,以距离 \(D_1,D_2\) 同时建二分图,然后染色之后就有 \(4\) 种颜色,根据鸽巢原理一定存在一个大小至少为 \(n^2\) 的同颜色点集,选出这个点集的任意 \(n^2\) 个点作为答案。
看错题了/kk,总之就是卒了,实际上要用代数证明。
以下是假证明:
定理一(皮克定理):对于一个顶点均为格点的简单多边形,设 \(S\) 为它的面积,内部格点个数为 \(n\),多边形边缘格点数为 \(s\),那么 \(S=n+\frac s 2-1\)。
推论:格点上任意一个简单多边形的面积为 \(\frac 1 2\) 的若干整数次倍,证明不言而喻。
对于边长为 \(a\) 的普通正三角形,其面积有公式 \(\frac{\sqrt{3}a^2}{4}\),若顶点均是格点,那么 \(a^2=x^2+y^2\),其是一个有理数,所以格点正三角形面积一定不是 \(\frac 1 2\) 的若干整数次倍,所以不存在格点正三角形。
正方形一定存在,证明不言而喻。
对于正五边形,我们假设现在已经求出了一个最小的格点正五边形 \(ABCDE\),由推论,这是一定存在的:
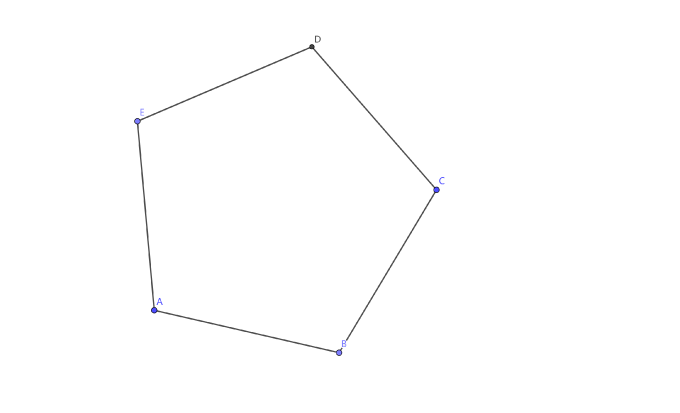
以这个格点正五边形的任意相邻的两边为基础,作平行四边形,会得到一个类五角星形式:
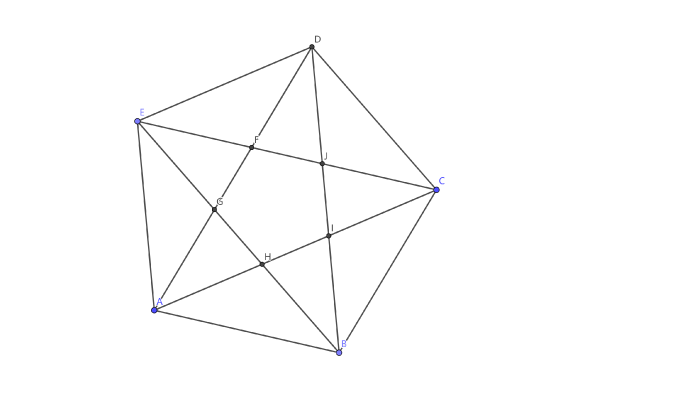
可以证明,正五边形 \(FGHIJ\) 为格点正五边形,并且其面积小于格点正五边形 \(ABCDE\)。正五边形是依靠平行四边形对角相等,而构造方式本质上是平移,所以也可以得到。
明明已经假设格点正五边形 \(ABCDE\) 为最小,但却又找到一个更小,这说明不存在格点正五边形。
对于正六边形,考虑如下格点正六边形 \(ABCDEF\):
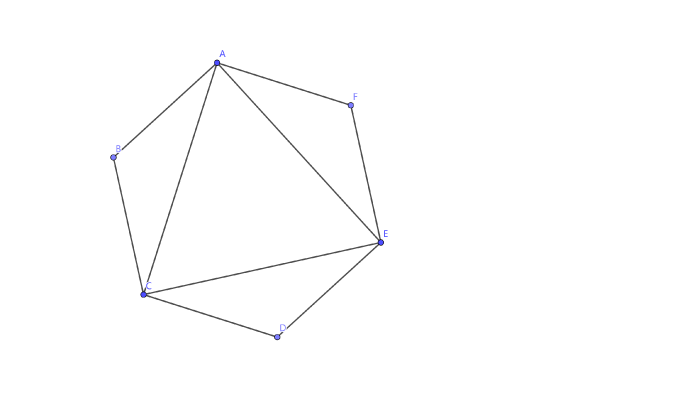
连接 \(AC,AE,CE\),可以得到一个格点正三角形,已经证明过不存在格点正三角形,那么也一定不存在格点正六边形。
现在处理所有正 \(k\) 边形,这里有 \(k\ge 7\),我们假设已经求出了一个最小的格点正 \(k\) 边形,设其边长为 \(a\),中心到每个点的距离为 \(b\)。
因为这些 \(k\) 边形的内角和均大于 \(120\) 度,所以 \(b>a\),考虑平移构造,我们将所有的边平移到共一个端点,并顺次连接另外一端,我们可以得到另一个格点正 \(k\) 边形,且其边长 \(c<a\),就此,我们给出一个更小的格点正 \(k\) 边形,这说明不存在格点正 \(k\) 边形。
就此,我们证明了,对于格点正多边形,仅存在格点正方形,这个结论严格包含于证明上面的这张图是二分图。
Code
/*
Author: cnyz
----------------
Looking! The blitz loop this planet to search way.
Only my RAILGUN can shoot it. 今すぐ
*/
#include<bits/stdc++.h>
using namespace std;
typedef double db;
typedef long long ll;
typedef pair<int,int> pii;
#define pb push_back
#define mp make_pair
#define fi first
#define se second
template <class T> void chkmax(T &x,T y) {
if(x<y) x=y;
}
template <class T> void chkmin(T &x,T y) {
if(x>y) x=y;
}
const int N=600;
int n,d1,d2;
vector<int> G[N*N+10];
bool vis[N*N+10];
int col[3][N*N+10];
void add(int u,int v) {
G[u].pb(v),G[v].pb(u);
}
int bh(int x,int y) {
return (x-1)*n+y;
}
void dfs(int u,int c,int id) {
col[id][u]=c,vis[u]=1;
for(auto v:G[u])
if(!vis[v])
dfs(v,c^1,id);
}
int cnt[5],X[5][N*N+10],Y[5][N*N+10];
int main() {
scanf("%d %d %d",&n,&d1,&d2);n*=2;
for(int i=0;i*i<=d1;i++) {
int j=sqrt(d1-i*i);
if(j*j+i*i!=d1) continue;
for(int x=1;x<=n;x++)
for(int y=1;y<=n;y++) {
if(x+i<=n&&y+j<=n) add(bh(x,y),bh(x+i,y+j));
if(x+i<=n&&y-j>0) add(bh(x,y),bh(x+i,y-j));
if(x-i>0&&y+j<=n) add(bh(x,y),bh(x-i,y+j));
if(x-i>0&&y-j>0) add(bh(x,y),bh(x-i,y-j));
if(x+j<=n&&y+i<=n) add(bh(x,y),bh(x+j,y+i));
if(x+j<=n&&y-i>0) add(bh(x,y),bh(x+j,y-i));
if(x-j>0&&y+i<=n) add(bh(x,y),bh(x-j,y+i));
if(x-j>0&&y-i>0) add(bh(x,y),bh(x-j,y-i));
}
}
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(!vis[bh(i,j)]) dfs(bh(i,j),0,1);
memset(vis,0,sizeof vis);
for(int x=1;x<=n;x++)
for(int y=1;y<=n;y++)
G[bh(x,y)].clear();
for(int i=0;i*i<=d2;i++) {
int j=sqrt(d2-i*i);
if(i*i+j*j!=d2) continue;
for(int x=1;x<=n;x++)
for(int y=1;y<=n;y++) {
if(x+i<=n&&y+j<=n) add(bh(x,y),bh(x+i,y+j));
if(x+i<=n&&y-j>0) add(bh(x,y),bh(x+i,y-j));
if(x-i>0&&y+j<=n) add(bh(x,y),bh(x-i,y+j));
if(x-i>0&&y-j>0) add(bh(x,y),bh(x-i,y-j));
if(x+j<=n&&y+i<=n) add(bh(x,y),bh(x+j,y+i));
if(x+j<=n&&y-i>0) add(bh(x,y),bh(x+j,y-i));
if(x-j>0&&y+i<=n) add(bh(x,y),bh(x-j,y+i));
if(x-j>0&&y-i>0) add(bh(x,y),bh(x-j,y-i));
}
}
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(!vis[bh(i,j)]) dfs(bh(i,j),0,2);
for(int x=1;x<=n;x++)
for(int y=1;y<=n;y++) {
int id=2*col[1][bh(x,y)]+col[2][bh(x,y)];
cnt[id]++;
X[id][cnt[id]]=x,Y[id][cnt[id]]=y;
if(cnt[id]==n*n/4) {
for(int i=1;i<=cnt[id];i++)
printf("%d %d\n",X[id][i]-1,Y[id][i]-1);
puts("");
return 0;
}
}
}
CF643F Bears and Juice [*2900]
有 \(n\) 个人玩游戏,在他们面前有若干桶水和恰好一桶未知液体,每个人每天选出这些桶的子集并喝下去一点,喝到未知液体的人会被请出游戏,人们的目标是求出未知液体是哪一桶。
如果被请出游戏的人超过 \(\min(p,n-1)\) 人的话游戏就失败了。
假设人都是绝顶聪明的,对于每一个天数,求出一个 \(R_i\) 表示最多的桶数使得经过若干天数后一定可以求出哪一桶是未知液体。
输出 \(\displaystyle \oplus^q_{i=1} i\times R_i \bmod 2^{32}\)。
Solution
我们要着眼于「信息」而不是题目本身,就像如何证明基于比较的排序算法的复杂度下界一样,我将做一下证明:
总共的信息个数为 \(n!\) 个,每一次比较会最多减少一半的信息,那么时间复杂度下界也就是 \(O(\log_2 (n!))\) 也就是 \(O(n\log_2 n)\)。
考虑假设有 \(i\) 天,那么信息总数就是 \(\displaystyle\sum^{\min(p,n-1)}_{j=0}\binom{n}{j}i^j\),意义是指从 \(n\) 个人中选出 \(j\) 个人,并且 \(j\) 个人选一天退出游戏。
接下来考虑能否「信息与确定一桶未知液体一一对应」,我们把第 \(i\) 条信息对应的未知液体称为第 \(i\) 桶未知液体,如果某个人在第 \(i\) 条信息没被请出游戏,那么他就不喝第 \(i\) 个桶,否则在它睡觉的哪天直接喝掉。
比如说 \(n=3,p=2,i=1\),信息如下:(用 \((x,y)\) 表示第 \(x\) 个人第 \(y\) 天被请出游戏。)
- 没有人被请出游戏;
- \((1,1)\);
- \((2,1)\);
- \((3,1)\);
- \((1,1)\),\((2,1)\);
- \((1,1)\),\((3,1)\);
- \((2,1)\),\((3,1)\)。
那么方案就是:(用 \((x,y)\) 表示第 \(x\) 个人喝第 \(y\) 桶)
- \((1,2),(2,3),(3,4)\);
- \((1,5),(2,5),(3,6)\);
- \((1,6),(2,6),(3,7)\)。
不难发现接下来就是暴力枚举,瓶颈在 \(\binom{n}{j}\) 上,这里直接暴力分解是可行的,时间复杂度 \(O(p^3\log n+pq)\)。
Code
const uint N=200;
uint n,p,q;
uint calc(int x) {
vector<uint> up,down;
up.clear(),down.clear();
for(uint i=1;i<=x;i++) up.pb(n-i+1),down.pb(i);
for(auto &i:up)
for(auto &j:down) {
uint d=__gcd(i,j);
i/=d,j/=d;
}
uint ret=1;
for(auto i:up) ret*=i;
return ret;
}
uint ans[N+10],out;
uint fpow(uint x,uint y) {
uint ret=1;
for(;y;y>>=1) {
if(y&1) ret*=x;
x*=x;
}
return ret;
}
int main() {
scanf("%d %d %d",&n,&p,&q);
for(uint i=0;i<=min(n-1,p);i++) ans[i]=calc(i);
for(uint i=1;i<=q;i++) {
uint sum=0;
for(uint j=0,k=1;j<=min(n-1,p);j++,k*=i) sum+=ans[j]*k;
out^=sum*i;
}
printf("%u\n",out);
}
CF1458C Latin Square [*2700]
Solution
如果只有上下左右,考虑维护左上角的位置的变化,显然这个变化可以推广到全局。
接下来考虑加入 I,C 之后如何处理,考虑一个 RI 的变化,首先 \(a_{i,j}=k\),R 之后 \(a_{i,j+1}=k\),I 之后 \(a_{i,k}=i+1\)。
考虑维护一个 \(x,y,z\),表示左上角的位置两维的变化,还有一个全局加标记。
对于上下左右,我们修改 \(x\) 或 \(y\),对于 I,C 交换 \(x/y,z\) 就可以了。
那么最后,我们只要处理掉 IC,然后处理变化即可。
不难发现连续的 I 或 C 无意义,可以直接消去,然后连续的 ICICIC 是不会有改变的,所以直接模 \(6\) 输出即可。
时间复杂度 \(O(n^2)\)。
Code
const int N=1000,M=1e5;
int n,m,a[N+10][N+10],top,b[N+10][N+10];
char ch[M+10],st[M+10];
int x,y,z;
void solve() {
scanf("%d %d",&n,&m);
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
scanf("%d",&a[i][j]),--a[i][j];
scanf("%s",ch+1);
x=0,y=0,z=0;
for(int i=1;i<=m;i++) {
if(ch[i]=='U') x=(x-1+n)%n;
if(ch[i]=='D') x=(x+1)%n;
if(ch[i]=='L') y=(y-1+n)%n;
if(ch[i]=='R') y=(y+1)%n;
if(ch[i]=='I') swap(y,z);
if(ch[i]=='C') swap(x,z);
}
top=0;
for(int i=1;i<=m;i++)
if(ch[i]=='I'||ch[i]=='C') {
if(st[top]==ch[i]) top--;
else st[++top]=ch[i];
}
top%=6;
for(int i=1;i<=top;i++) {
if(st[i]=='I')
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
b[i][a[i][j]]=j;
if(st[i]=='C')
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
b[a[i][j]][j]=i;
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
a[i][j]=b[i][j];
}
for(int i=0;i<n;i++) {
for(int j=0;j<n;j++)
printf("%d ",(a[(i-x+n)%n][(j-y+n)%n]+z)%n+1);
puts("");
}
}