In an infinite binary tree where every node has two children, the nodes are labelled in row order.
In the odd numbered rows (ie., the first, third, fifth,...), the labelling is left to right, while in the even numbered rows (second, fourth, sixth,...), the labelling is right to left.
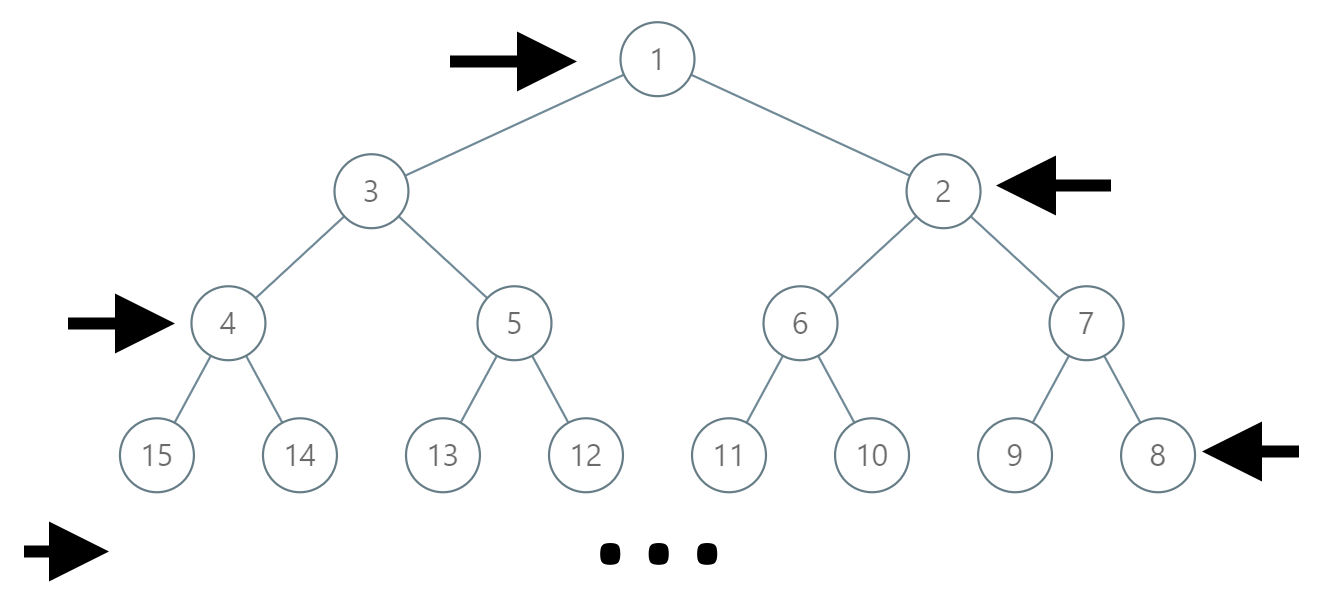
Given the label of a node in this tree, return the labels in the path from the root of the tree to the node with that label.
Example 1:
Input: label = 14 Output: [1,3,4,14]
Example 2:
Input: label = 26 Output: [1,2,6,10,26]
Constraints:
1 <= label <= 10^6
二叉树寻路。
在一棵无限的二叉树上,每个节点都有两个子节点,树中的节点 逐行 依次按 “之” 字形进行标记。
如下图所示,在奇数行(即,第一行、第三行、第五行……)中,按从左到右的顺序进行标记;
而偶数行(即,第二行、第四行、第六行……)中,按从右到左的顺序进行标记。
给你树上某一个节点的标号
label,请你返回从根节点到该标号为label节点的路径,该路径是由途经的节点标号所组成的。来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/path-in-zigzag-labelled-binary-tree
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
这道题算是数学 + 递归吧。我参考了这个帖子。如果是一棵正常的二叉树(每一层都是从左往右),每个节点的父节点就是当前节点的 label / 2。但是注意这棵树的节点是之字形的,所以如果根节点的层数我们定义为0的话,偶数层的节点都是从右往左递增的,并且最外层的两个节点的和 = 内层的两个节点的和。如果把这棵树从父节点左右对折,所有相同层上对应的点的加和都应该是一样的。比如4 + 7 = 5 + 6;15 + 8 = 14 + 9 = 13 + 10 = 12 + 11等等。
因为这棵树是满二叉树,所以如果知道当前的层数 depth,那么我们很容易就可以知道当前层的最大最小节点值(因为可以知道上一层的最大值是多少),这样也就知道了某一个节点的对称点的值是多少了。
举个例子,比如在一个正常的树中,14 的父节点本应该是 7,但是因为是之字形的关系,实际 14 的父节点在之字形里应该是 4,但是这个 4 是怎么计算出来的呢?14 / 2 = 7,然后有因为我们知道了 14 的上一层,也就是 7 所在的这一层(level = 3)的
- 最大节点值是 2^3 - 1 = 7
- level = 3 的节点个数 = 2 ^ (3 - 1) = 2 ^ 2 = 4
- 最小节点值是 7 - 4 + 1 = 4,所以得出 14 的父节点是 4。
时间O(n)
空间O(n)
Java实现
1 class Solution { 2 public List<Integer> pathInZigZagTree(int label) { 3 List<Integer> res = new ArrayList<>(); 4 int depth = 0; 5 while (Math.pow(2, depth) - 1 < label) { 6 depth++; 7 } 8 depth--; 9 while (depth != 0) { 10 res.add(0, label); 11 int pos = label - (int) Math.pow(2, depth); 12 label = label - (pos + 1) - pos / 2; 13 depth--; 14 } 15 res.add(0, 1); 16 return res; 17 } 18 }
二刷的时候我自己也写了一种更好理解的做法。
1 class Solution { 2 public List<Integer> pathInZigZagTree(int label) { 3 List<Integer> res = new ArrayList<>(); 4 int depth = 0; 5 while (Math.pow(2, depth) - 1 < label) { 6 depth++; 7 } 8 depth--; 9 while (depth != 0) { 10 res.add(0, label); 11 int maxVal = (int) Math.pow(2, depth) - 1; // 上一层的最大值 12 int nodes = (int) Math.pow(2, depth - 1); // 上一层的节点个数 13 int minVal = maxVal - nodes + 1; // 上一层的最小值 14 int levelSum = maxVal + minVal; // 上一层每对node的和 15 label = levelSum - label / 2; // 找到label的父节点的对应node.val 16 depth--; 17 } 18 res.add(0, 1); 19 return res; 20 } 21 }