There is a ball in a maze with empty spaces and walls. The ball can go through empty spaces by rolling up (u), down (d), left (l) or right (r), but it won't stop rolling until hitting a wall. When the ball stops, it could choose the next direction. There is also a hole in this maze. The ball will drop into the hole if it rolls on to the hole.
Given the ball position, the hole position and the maze, find out how the ball could drop into the hole by moving the shortest distance. The distance is defined by the number of empty spaces traveled by the ball from the start position (excluded) to the hole (included). Output the moving directions by using 'u', 'd', 'l' and 'r'. Since there could be several different shortest ways, you should output the lexicographically smallest way. If the ball cannot reach the hole, output "impossible".
The maze is represented by a binary 2D array. 1 means the wall and 0 means the empty space. You may assume that the borders of the maze are all walls. The ball and the hole coordinates are represented by row and column indexes.
Example 1:
Input 1: a maze represented by a 2D array 0 0 0 0 0 1 1 0 0 1 0 0 0 0 0 0 1 0 0 1 0 1 0 0 0 Input 2: ball coordinate (rowBall, colBall) = (4, 3) Input 3: hole coordinate (rowHole, colHole) = (0, 1) Output: "lul" Explanation: There are two shortest ways for the ball to drop into the hole. The first way is left -> up -> left, represented by "lul". The second way is up -> left, represented by 'ul'. Both ways have shortest distance 6, but the first way is lexicographically smaller because 'l' < 'u'. So the output is "lul".
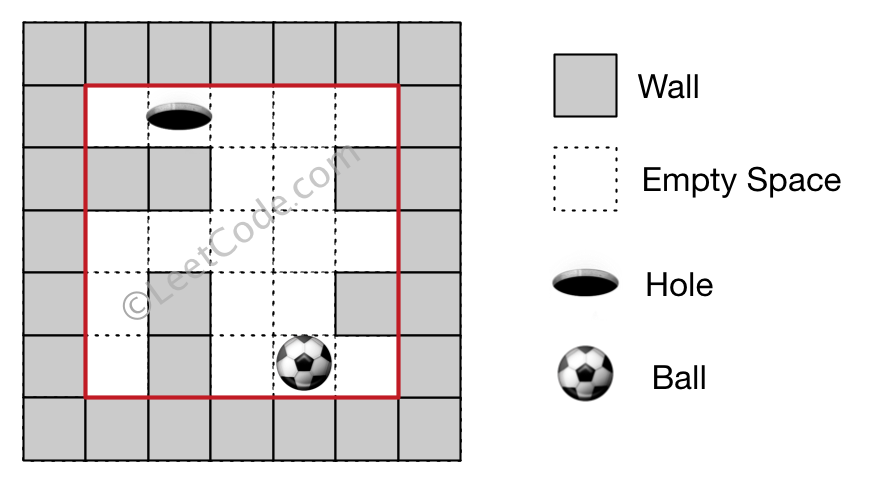
Example 2:
Input 1: a maze represented by a 2D array 0 0 0 0 0 1 1 0 0 1 0 0 0 0 0 0 1 0 0 1 0 1 0 0 0 Input 2: ball coordinate (rowBall, colBall) = (4, 3) Input 3: hole coordinate (rowHole, colHole) = (3, 0) Output: "impossible" Explanation: The ball cannot reach the hole.
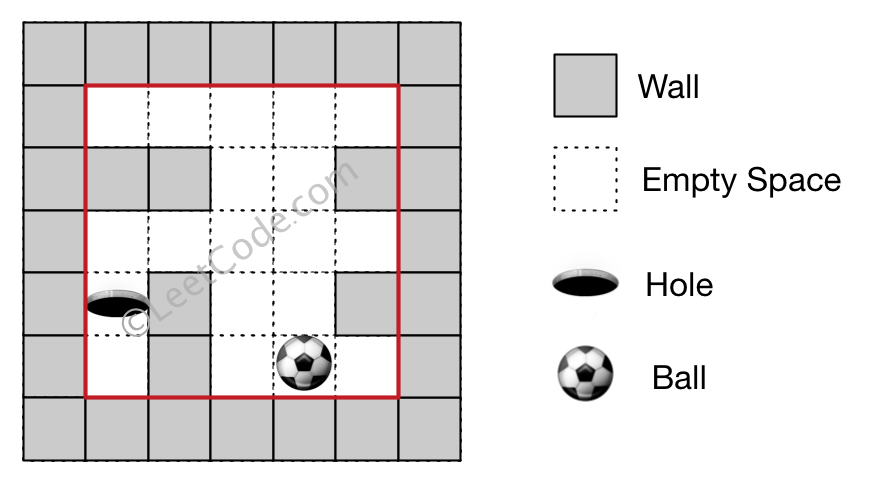
Note:
- There is only one ball and one hole in the maze.
- Both the ball and hole exist on an empty space, and they will not be at the same position initially.
- The given maze does not contain border (like the red rectangle in the example pictures), but you could assume the border of the maze are all walls.
- The maze contains at least 2 empty spaces, and the width and the height of the maze won't exceed 30.
迷宫III。题意跟前两个版本类似,多一个条件,矩阵中有一个坐标hole代表一个洞,问的是球是否能按规则移动最后掉入洞口,若能则输出字典序最小的路径,若不能则输出impossible。
思路还是BFS,但是具体写的时候有一些细节需要注意。
如果遍历的过程中,有遇到hole的坐标则立即break,开始结算路径
路径的长度这样算:起点和终点的横纵坐标的绝对值的差
用compareTo来比较字典序
代码非常琐碎,面试不太容易写的对
时间O(mn)
空间O(n)
Java实现
1 class Solution { 2 public String findShortestWay(int[][] maze, int[] ball, int[] hole) { 3 int m = maze.length; 4 int n = maze[0].length; 5 String[][] way = new String[m][n]; 6 for (int i = 0; i < m; i++) { 7 for (int j = 0; j < n; j++) { 8 way[i][j] = ""; 9 } 10 } 11 12 int[][] dp = new int[m][n]; 13 int[] dx = new int[] { -1, 1, 0, 0 }; 14 int[] dy = new int[] { 0, 0, -1, 1 }; 15 String[] dircectStr = new String[] { "u", "d", "l", "r" }; 16 Queue<int[]> queue = new LinkedList<>(); 17 queue.offer(ball); 18 while (!queue.isEmpty()) { 19 int[] cur = queue.poll(); 20 for (int direction = 0; direction < 4; direction++) { 21 int nx = cur[0]; 22 int ny = cur[1]; 23 while (nx >= 0 && nx < n && ny >= 0 && ny < m && maze[nx][ny] == 0) { 24 if (nx == hole[0] && ny == hole[1]) { 25 nx += dx[direction]; 26 ny += dy[direction]; 27 break; 28 } 29 nx += dx[direction]; 30 ny += dy[direction]; 31 } 32 nx -= dx[direction]; 33 ny -= dy[direction]; 34 int steps = dp[cur[0]][cur[1]] + Math.abs(nx - cur[0]) + Math.abs(ny - cur[1]); 35 // 非当前位置,未初始化,路径长度小于当前位置的原来的值,路径长度相等,字典序更小 36 if (!(nx == cur[0] && ny == cur[1]) && (dp[nx][ny] == 0 || (dp[nx][ny] > steps || (dp[nx][ny] == steps 37 && (way[cur[0]][cur[1]] + dircectStr[direction]).compareTo(way[nx][ny]) < 0)))) { 38 dp[nx][ny] = steps; 39 way[nx][ny] = way[cur[0]][cur[1]] + dircectStr[direction]; 40 if (!(nx == hole[0] && ny == hole[1])) { 41 queue.offer(new int[] { nx, ny }); 42 } 43 } 44 } 45 } 46 return way[hole[0]][hole[1]].equals("") ? "impossible" : way[hole[0]][hole[1]]; 47 } 48 }