[LeetCode] 77. Combinations

Given two integers n and k, return all possible combinations of k numbers out of the range [1, n].

You may return the answer in any order.

Example 1:

Input: n = 4, k = 2
Output:
[
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
]

Example 2:

Input: n = 1, k = 1
Output: [[1]]

Constraints:

1 <= n <= 20
1 <= k <= n

组合。

题意是给一个数字 N 和一个数字 K，请你返回 1 ... n 中所有可能的 k 个数的组合。

分享一个写的很好的帖子。依然是 backtracking 类的题目，注意这里 N 的下限是从 1 开始。同时这个题又规定了 combination 的数字个数只能为 K 个所以 helper 函数的退出条件是 K == 0。

题目为什么会意识到是 backtracking 类型是因为需要寻找全部/多种组合，这种需要试探所有可能性的题会比较偏向 DFS/backtracking。为了避免结果的重复或者漏解，我们可能需要对 input 先做排序，但是这道题因为我们一会遍历的时候是从 1 往 N 走的，实现了自行有序，所以无需排序。一些关于字符串排列组合的题可能就需要排序了。

时间O(n^min(k, n - k))

空间O(n)

Java实现

 1 class Solution {
 2     public List<List<Integer>> combine(int n, int k) {
 3         List<List<Integer>> res = new ArrayList<>();
 4         helper(res, new ArrayList<>(), n, k, 1);
 5         return res;
 6     }
 7 
 8     private void helper(List<List<Integer>> res, List<Integer> list, int n, int k, int start) {
 9         // 退出条件，当res里的个数满足K了，就加入结果集
10         if (k == 0) {
11             res.add(new ArrayList<>(list));
12             return;
13         }
14         // 选取一个数字作为组合的第一个数字，直到N
15         for (int i = start; i <= n; i++) {
16             list.add(i);
17             // 递归的下一层里面K就减1，但是同时开始的index也需要 + 1
18             helper(res, list, n, k - 1, i + 1);
19             list.remove(list.size() - 1);
20         }
21     }
22 }

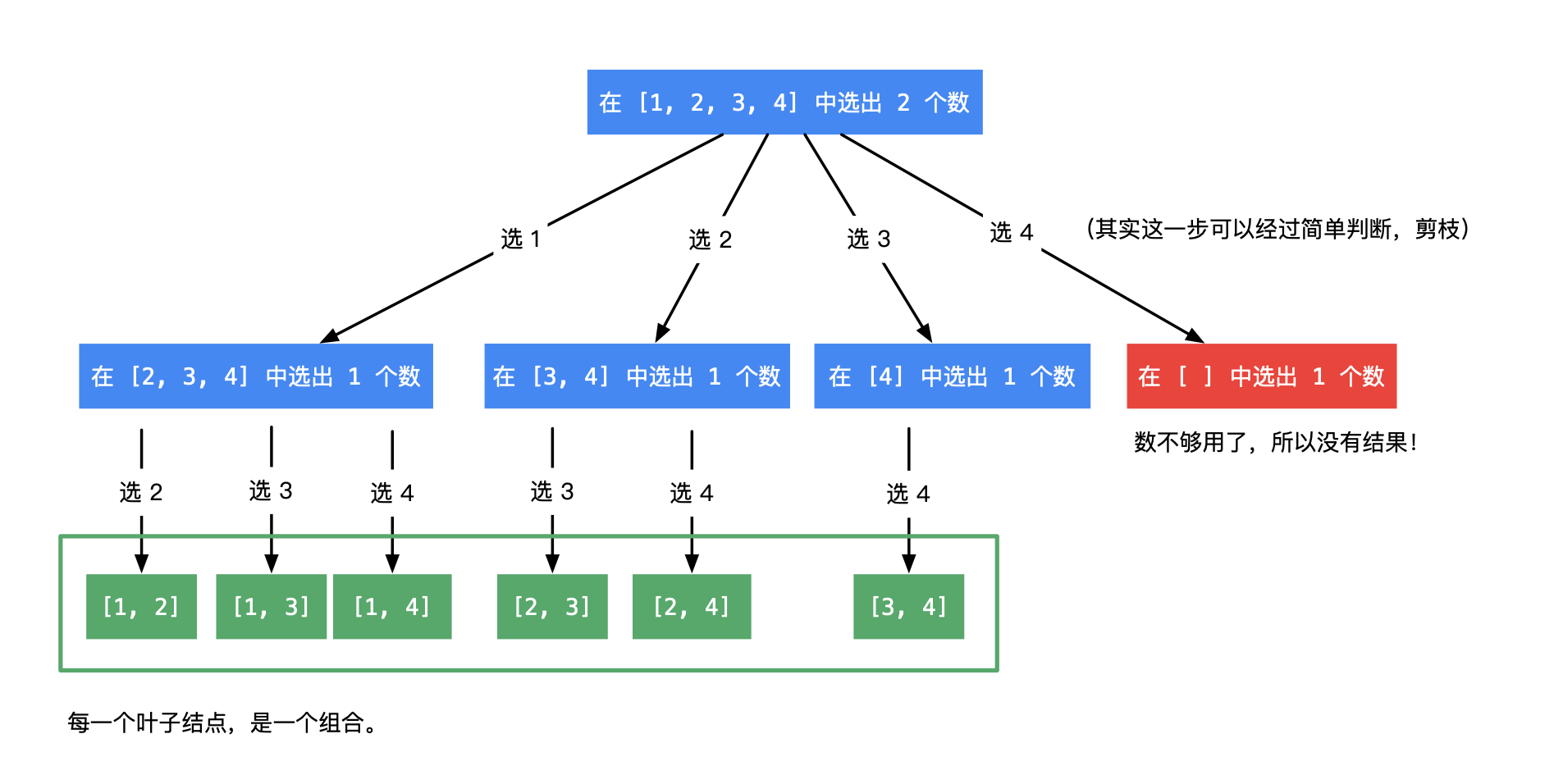
同时我附上这个截图，根据起点画出的二叉树对于解决这个问题很有帮助。