Given a binary tree where each path going from the root to any leaf form a valid sequence, check if a given string is a valid sequence in such binary tree.
We get the given string from the concatenation of an array of integers arr and the concatenation of all values of the nodes along a path results in a sequence in the given binary tree.
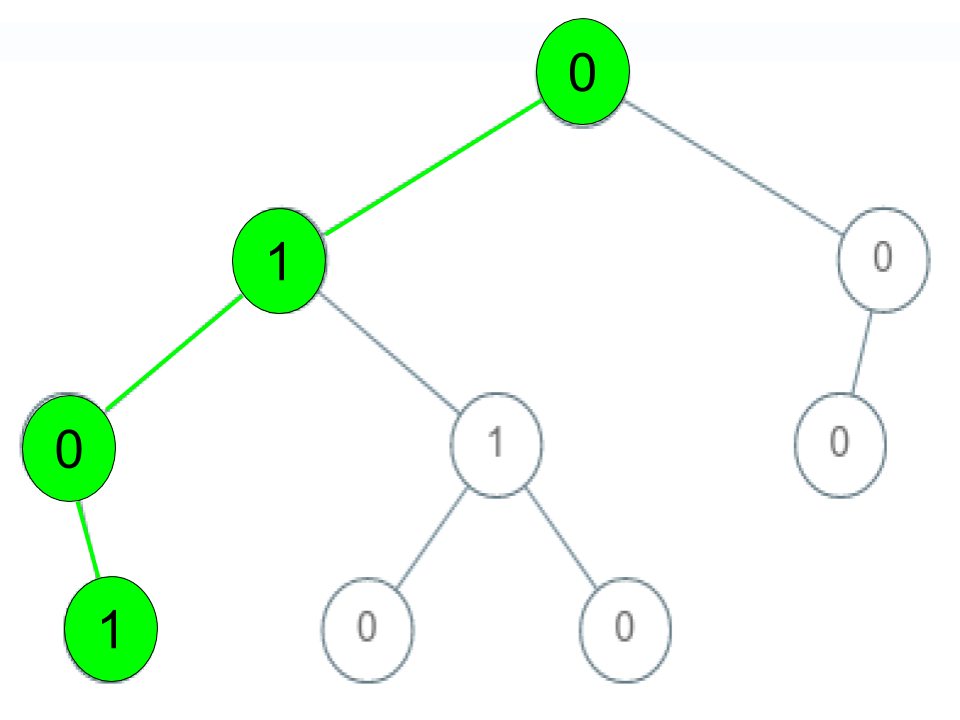
Input: root = [0,1,0,0,1,0,null,null,1,0,0], arr = [0,1,0,1] Output: true Explanation: The path 0 -> 1 -> 0 -> 1 is a valid sequence (green color in the figure). Other valid sequences are: 0 -> 1 -> 1 -> 0 0 -> 0 -> 0
题意是给一个二叉树和一个从根节点开始的sequence,请你判断这个sequence是否是一个有效的,从根节点到某个叶子节点的sequence。我只放一个例子好了,因为这个题比较直观。如果给出的sequence arr少任何一个节点,都要return false。
思路是DFS深度遍历。如果遍历到的当前节点没有左孩子也没有右孩子,说明是叶子节点了,则判断此时的深度 + 1是不是跟遍历arr的长度一致。需要检查的corner case有
- 当前深度大于arr.length
- 当前节点上的值跟遍历到的arr[index]不一样
- 当前节点为空 - 事实上在路径中的任何一个节点都不能为空
时间O(n)
空间O(n)
Java实现
1 /** 2 * Definition for a binary tree node. 3 * public class TreeNode { 4 * int val; 5 * TreeNode left; 6 * TreeNode right; 7 * TreeNode() {} 8 * TreeNode(int val) { this.val = val; } 9 * TreeNode(int val, TreeNode left, TreeNode right) { 10 * this.val = val; 11 * this.left = left; 12 * this.right = right; 13 * } 14 * } 15 */ 16 class Solution { 17 public boolean isValidSequence(TreeNode root, int[] arr) { 18 return dfs(root, arr, 0); 19 } 20 21 private boolean dfs(TreeNode n, int[] a, int depth) { 22 if (n == null || depth >= a.length || a[depth] != n.val) { // base cases. 23 return false; 24 }// key base case: a leave found. 25 if (n.left == null && n.right == null) { // credit to @The_Legend_ for making the code clean 26 return depth + 1 == a.length; // valid sequence? 27 } 28 return dfs(n.left, a, depth + 1) || dfs(n.right, a, depth + 1); // recurse to the children. 29 } 30 }