Balancing Act
时限:1000ms
Description
Consider a tree T with N (1 <= N <= 20,000) nodes numbered 1...N. Deleting any node from the tree yields a forest: a collection of one or more trees. Define the balance of a node to be the size of the largest tree in the forest T created by deleting that node from T.
For example, consider the tree:
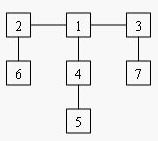
Deleting node 4 yields two trees whose member nodes are {5} and {1,2,3,6,7}. The larger of these two trees has five nodes, thus the balance of node 4 is five. Deleting node 1 yields a forest of three trees of equal size: {2,6}, {3,7}, and {4,5}. Each of these trees has two nodes, so the balance of node 1 is two.
For each input tree, calculate the node that has the minimum balance. If multiple nodes have equal balance, output the one with the lowest number.
For example, consider the tree:

Deleting node 4 yields two trees whose member nodes are {5} and {1,2,3,6,7}. The larger of these two trees has five nodes, thus the balance of node 4 is five. Deleting node 1 yields a forest of three trees of equal size: {2,6}, {3,7}, and {4,5}. Each of these trees has two nodes, so the balance of node 1 is two.
For each input tree, calculate the node that has the minimum balance. If multiple nodes have equal balance, output the one with the lowest number.
Input
The first line of input contains a single integer t (1 <= t <= 20), the number of test cases. The first line of each test case contains an integer N (1 <= N <= 20,000), the number of congruence. The next N-1 lines each contains two space-separated node numbers that are the endpoints of an edge in the tree. No edge will be listed twice, and all edges will be listed.
Output
For each test case, print a line containing two integers, the number of the node with minimum balance and the balance of that node.
Sample Input
1 7 2 6 1 2 1 4 4 5 3 7 3 1
Sample Output
1 2
树的重心也叫树的质心。找到一个点,其所有的子树中最大的子树节点数最少,那么这个点就是这棵树的重心,删去重心后,生成的多棵树尽可能平衡。
利用树形dp的思想,对节点u的子树进行遍历。和树的直径不同的是,如果子树的分割确定了,那么子树之外的节点必定在一颗树上,不需要在dfs一次。
#include "stdio.h" #include "algorithm" #include "string.h" using namespace std; const int INF = 0x3f3f3f3f; const int maxn = 20000 + 10; bool vis[maxn]; struct edge { int to, next; } e[maxn*2]; int n, num[maxn]; int size, cur; int tot = 0; int head[maxn]; void add_edge(int u, int v) { e[tot].to = v; e[tot].next = head[u]; head[u] = tot++; } void dfs(int u) { num[u] = 0; int tr = 0; vis[u] = true; for (int i = head[u]; i != -1; i = e[i].next) { int v = e[i].to; if (vis[v]) continue; dfs(v); num[u] += num[v] + 1; tr = max(num[v] + 1, tr); } tr = max(n - num[u] - 1, tr); //剩下那棵树的大小 if (tr < size || tr == size && cur > u) { //答案还要编号节点最小 size = tr; cur = u; } } void init() { memset(vis, false, sizeof(vis)); memset(head, -1, sizeof(head)); tot = 0; size = INF; } int main(int argc, char const *argv[]) { int T; scanf("%d", &T); while (T--) { init(); scanf("%d", &n); for (int i = 0; i < n-1; i++) { int u, v; scanf("%d%d", &u, &v); add_edge(u, v); add_edge(v, u); } dfs(1); printf("%d %d ", cur, size); } return 0; }