1.题意:1到N的序列的排列中,元素位置与元素值相对应的情况(值为i的元素在某个排列中正好排在第i个位置)大于等于序列规模一半的情况,有多少个?
2.输入输出:每组数据一个数,N,规定输入以0结尾;
3.分析:原题意换句话说,就是针对1到N的全排列,错排元素的个数小于等于N的情况有多少;
那么,输出即为: 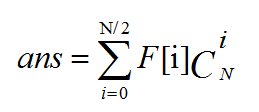 ,其中F[i]表示1到i的错排方案数,后面一项为组合数,即选取i个错排;
,其中F[i]表示1到i的错排方案数,后面一项为组合数,即选取i个错排;
这里推导一下错排公式,F[N]表示1到N的错排方案;第一步:选取N放到1到N-1之中任意一个位置,这样就有N-1种放法;第二步:分两种情况,不妨设第一步被N占据的位置为K,当位置N放置的数恰巧为K时,此时就相当于,K,N交换位置了,对应的错排方案为F[N-2];当位置N放置的数不为K时,此时的情况:1到K-1,K+1到N的位置要错排放置1到N-1的元素,N-1个 位置,N-1个元素,与F[N-1]的情况相比,只是多了一组(数K与位置N)的对应,而且这里N不放置K,就等效于普通的情况下(数K与位置K)的错排情况;举个例子,位置12345,数12345,现在5放置在2的位置上,剩下数1234,位置1345,且位置5上不放2,这里和1234-1234的错排有什么区别么?把位置5当成位置2,反正也是2不放在位置5上,与1234-1234里2不放在位置2上等效;综上所述,错排公式为F[i]=(i-1)*(F[i-1]+F[i-2]),其中,F[1]=0,F[2]=1;
1 # include <iostream> 2 # include <cstdio> 3 using namespace std; 4 const int MAXN=26; 5 int dp[MAXN]; 6 int N; 7 long long Cn(int n,int m) 8 { 9 if(n==0) return 1; 10 n=m-n>n?n:m-n; 11 long long up,down; 12 up=down=1; 13 for(int i=1;i<=n;i++) 14 { 15 up*=m-i+1; 16 down*=i; 17 } 18 long long res=up/down; 19 return res; 20 } 21 void Init() 22 { 23 dp[0]=1; 24 dp[1]=0; 25 dp[2]=1; 26 for(int i=3;i<15;i++) 27 dp[i]=(i-1)*(dp[i-1]+dp[i-2]); 28 } 29 int main() 30 { 31 Init(); 32 while(scanf("%d",&N)!=EOF) 33 { 34 if(N==0) break; 35 long long res=0; 36 for(int i=0;i<=N/2;i++) 37 res+=dp[i]*Cn(i,N); 38 printf("%lld ",res); 39 } 40 return 0; 41 }