Splay Tree(伸展树)
简介
Splay Tree是一种二叉查找树(BST),即满足二叉树上任意一个节点的左儿子权值>自身权值>右儿子权值,它通过旋转操作使得树上单次操作的均摊复杂度为 (log n),由Daniel Sleator和Robert Endre Tarjan(又是Tarjan)发明,希望了解复杂度证明的可以自行查询资料(我不会证)
实现
存储、维护与更新
一般我们把树上的每一个节点都作为结构体存放,节点中维护当前节点对应的值,当前节点对应值的个数,两个子节点的编号,子树中节点的个数以及父节点编号
为了实现方便,常用 (ch[0]) 或 (son[0]) 表示左儿子,用 (ch[1]) 或 (son[1]) 表示右儿子
struct Node
{
int v,cnt,siz,fa,ch[2];//节点值,个数,子树及自身节点个数,父亲,儿子 0->left 1->right
};
实现中常常需要改变节点间的关系,我们需要从子节点更新当前节点的信息
void update(int x)
{
node[x].siz=node[node[x].ch[0]].siz+node[node[x].ch[1]].siz+node[x].cnt;
}
旋转
旋转可以说是Splay的基础,利用旋转才能让树保持平衡,Splay中有左旋(Left Rotation)和右旋(Right Rotation),如下图
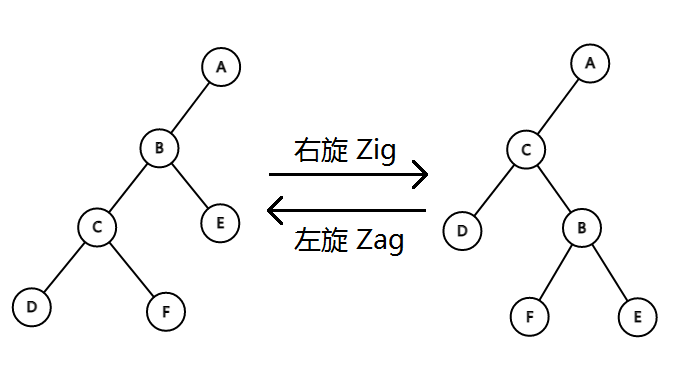
不难发现,旋转操作需要让树仍然满足二叉查找树的性质
具体地说,例如在这张图中,右旋C节点我们就需要 1.用C替换B成为A的子节点 2.把C的右儿子作为B的左儿子 3.把B作为C的右儿子
右旋B节点我们就需要 1.用B替换C成为A的子节点 2.把B的左儿子作为C的右儿子 3.把C作为B的左儿子
void rotate(int x)
{
int y=node[x].fa,z=node[y].fa,k=(node[y].ch[1]==x);//y是x的父亲,z是y的父亲,k表示x是不是y的左儿子
node[z].ch[node[z].ch[1]==y]=x;//用x替换y作为z的儿子
node[x].fa=z;
node[y].ch[k]=node[x].ch[k^1];//把x的对应儿子转移给y
node[node[x].ch[k^1]].fa=y;
node[x].ch[k^1]=y;//把y更新为x的儿子
node[y].fa=x;
update(y),update(x);//y是x的子节点所以必须先更新y再更新x
}
代码中 ^1 表示异或1,其中 1^1=0 ,0^1=1,也就是取反的意思
伸展(Splay)
Splay操作即为把一个节点通过不断旋转旋转到根,每次查询或者修改操作后都将操作的节点Splay到根就能保证单次操作复杂度均摊为 (log n)
但是我们不能单纯地把节点不断向上转,考虑如下这种情况,我们想把C转到根
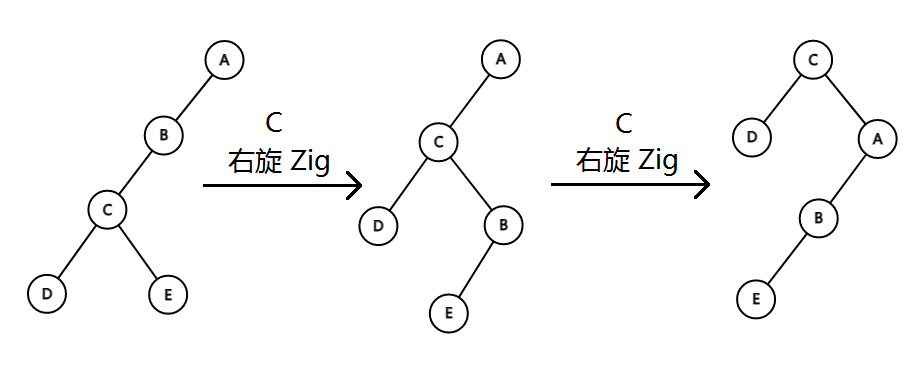
我们发现如果单纯把C向上转的话,如果原本是链,转动之后还是链,并不能优化,所以我们需要双旋,也就是在当前节点和当前节点的父节点都是自己父节点的左儿子或者右儿子时,我们先转动当前节点的父节点,再转动当前节点,如下图
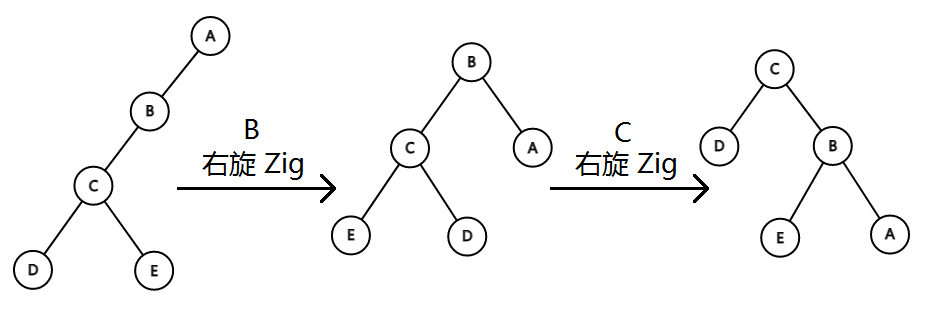
这样就让单次操作复杂度均摊到了 (log n),代码实现如下
void splay(int x,int target)//让x成为target的子节点,根节点是节点0的子节点
{
while(node[x].fa!=target)//转到目标就停止
{
int y=node[x].fa,z=node[y].fa;
if(z!=target)//如果转一下就满足就不多转一次
((node[z].ch[0]==y)^(node[y].ch[0]==x))?rotate(x):rotate(y);//三点为链就转y否则转x
rotate(x);//转一下x
}
if(!target)Root=x;//如果是转到根就更新根
}
插入
插入一个新节点要先从根据插入节点与当前找到的节点的大小关系从根节点开始向两个子节点走,直到找到插入节点值与当前节点相等,或者当前找到的节点编号不存在(即这个值从未出现过),然后更新信息即可
具体实现很好理解,看代码
void insert(int x)//插入x
{
int cur=Root,from=0;//当前找到的节点编号cur以及节点来源from
while(cur&&x!=node[cur].v)//找到了有相同值或者进入了未定义节点就停下
from=cur,cur=node[cur].ch[x>node[cur].v];//往子节点走
if(cur)//已经存在就增加个数即可
++node[cur].cnt;
else//创建新节点
{
cur=++node_cnt;//分配新编号
if(!from) Root=cur;//是根就更新根信息
else node[from].ch[x>node[from].v]=cur;//不是根就更新父节点信息
//更新新节点信息
node[cur].v=x;
node[cur].cnt=1;
node[cur].fa=from;
node[cur].siz=1;
node[cur].ch[0]=node[cur].ch[1]=0;
}
splay(cur,0);//转到根
}
查找
查找操作就是在树上找一个值对应的节点,并且把这个节点转到根,方便进行操作,不断往下找就行,看代码
void find(int x)//查找元素,调用后根即为查找的元素
{
int cur=Root;//从根开始查
if(!cur)return;//树为空就退出
while(node[cur].ch[x>node[cur].v]&&x!=node[cur].v)
//x不是当前节点值且当前节点有更小或更大值就进入子节点继续找
cur=node[cur].ch[x>node[cur].v];//进入子节点
splay(cur,0);//将找到的节点转到根
}
查找前驱后继
前驱定义为比一个数小的数中最大的,后继定义为比一个数大的数中最小的
直接把要查找的值对应的节点转到根,要查前驱就从左儿子开始一直往右找,要查后继就从右儿子开始一直往左找,非常简单
int find_pre_id(int x)//查前驱编号
{
find(x);//转到根
if(node[Root].v<x)return Root;//原树中没有这个值,就直接返回根
int cur=node[Root].ch[0];//进左子树
while(node[cur].ch[1]) cur=node[cur].ch[1];//往右
return cur;
}
int find_nxt_id(int x)//查后继编号
{
find(x);//转到根
if(node[Root].v>x)return Root;//原树中没有这个值,就直接返回根
int cur=node[Root].ch[1];//进右子树
while(node[cur].ch[0]) cur=node[cur].ch[0];//往左
return cur;
}
int find_pre(int x)//查前驱值
{
x=find_pre_id(x);//找到前驱编号
return node[x].v;//返回值
}
int find_nxt(int x)//查后继值
{
x=find_nxt_id(x);//找到后继编号
return node[x].v;//返回值
}
查数的排名
排名定义为比一个数小的数的个数+1,只需要将这个数转到根,返回比它左儿子的 (size) 即可(因为已经插入了极小值,所以不需要再多+1),如果没有找到这个值,那么显然当前的根节点就是这个数的前驱或者后继,分类讨论一下,如果是后继那么显然后继的排名和当前值的排名没有区别,如果是前驱那么自己的排名就是左儿子的 (size) 加上自己的 (cnt)
int get_rank(int x)
{
find(x);//转到根
//比它小的数的个数+1就是排名,这里因为我们插入了极小值就不用+1了
if(node[Root].v>=x)//根为后继那么排名是一样的
return node[node[Root].ch[0]].siz;
return node[node[Root].ch[0]].siz+node[Root].cnt;//根为前驱那么排名加上根的cnt就可以了
}
查排名对应的数
我们从根节点开始找,左边和当前节点个数小于排名,就说明这个数一定在右子树,我们把排名减去左边和当前节点个数然后进入右子树查询新排名
如果左子树节点更多就直接进左子树查
否则当前找到的节点就是对应的数,返回即可
int kth(int rank)//查排名为k的数
{
++rank;//这里因为我们插入了极小值,排名需要+1
int cur=Root,son;//cur从根开始,son为当前节点的右儿子
if(node[cur].siz<rank) return -1;//没有这么多数就退出
while(1)
{
son=node[cur].ch[0];
if(rank>node[son].siz+node[cur].cnt)//左边和当前节点个数不到k
{
rank-=node[son].siz+node[cur].cnt;//减去这么多个
cur=node[cur].ch[1];//进入右子树
}
else if(node[son].siz>=rank) cur=son;//左子树节点更多就进左子树查
else return node[cur].v;//找到了就返回
}
}
删除
删除操作较为复杂,我们先找到要删除数的前驱和后继,把前驱转到根,后继转到根节点也就是前驱的子节点,此时显然有后继是前驱的右儿子,后继的左儿子一定大于前驱小于后继,也就是我们要删除的数,根据前驱和后继的定义,后继一定有且仅有一个左儿子,对这个节点进行删除即可
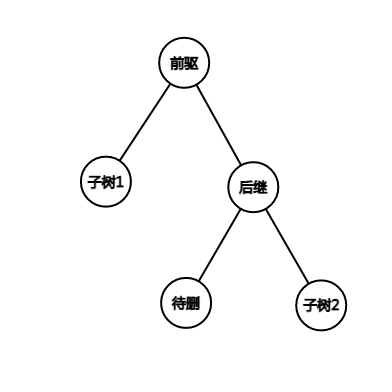
void erase(int x)
{
int x_pre=find_pre_id(x),x_nxt=find_nxt_id(x);//找x的前驱后继
splay(x_pre,0);//把前驱转到根
splay(x_nxt,x_pre);//把后继转到根的子节点
int cur=node[x_nxt].ch[0];//此时x一定是后继的左儿子
if(node[cur].cnt>1)//删不完
{
--node[cur].cnt;//减少一个
splay(cur,0);//转
}
else node[x_nxt].ch[0]=0;//切断后继的左子树
}
区间翻转
能支持区间翻转(即把区间内所有数换个位置,第一个与最后一个交换,第二个与倒数第二个交换……以此类推)是Splay Tree的一大特性,为了实现区间翻转,Splay Tree上维护的就不再是权值,而改为维护下标
对于一次区间翻转操作,我们利用刚刚提到的删除操作的类似思想,把区间的前驱旋转成为根,把区间的后继旋转成为根节点的右儿子,这时整个区间就成为了根的右儿子的左儿子的这棵子树,我们给树上的每一个节点都维护一个标记,表示它以及它的子树是否被翻转,每次一旦对于节点有操作,我们就把标记向下传递,同时交换自己的左右儿子并清除自身标记
PS:这里找区间的前驱后继记得检查你是否更改了自己的查询 (k) 大数函数,这个函数的返回值应该改为树上节点的下标而不是所维护的 (v)
在查询最后结果时只需要中序遍历整棵Splay Tree就可以获得整棵树操作后的编号顺序
struct Node
{
_Tp v;
int cnt,siz,fa,ch[2];
bool mark;//维护的翻转标记
};
void push_down(int x)//下传标记
{
if(node[x].mark)//如果有标记
{
//更新左右儿子标记(翻转两次就等于不翻转,清除标记)
node[node[x].ch[0]].mark^=1;
node[node[x].ch[1]].mark^=1;
node[x].mark=0;//清除自身标记
swap(node[x].ch[0],node[x].ch[1]);//交换左右儿子
}
}
void mid_find(int x)//中序遍历
{
push_down(x);//遍历时所有标记都要下传
if(node[x].ch[0]) mid_find(node[x].ch[0]);
if(node[x].v>0&&node[x].v<=n) write(node[x].v,' ');
if(node[x].ch[1]) mid_find(node[x].ch[1]);
}
int new_kth(int rank)//更改后的查询第k大数
{
++rank;
int cur=Root,son;
if(node[cur].siz<rank) return INF;
while(1)
{
push_down(cur);
son=node[cur].ch[0];
if(rank>node[son].siz+node[cur].cnt)
{
rank-=node[son].siz+node[cur].cnt;
cur=node[cur].ch[1];
}
else if(node[son].siz>=rank) cur=son;
else return cur;//在这里修改为返回下标!不要返回v
}
}
void reverse(int l,int r)//区间翻转(l到r)
{
l=tre.kth(l-1);//找区间前驱后继
r=tre.kth(r+1);
tre.splay(l,0);//把区间前驱后继Splay上来
tre.splay(r,l);
tre.node[tre.node[tre.node[tre.Root].ch[1]].ch[0]].mark^=1;
//根节点的右儿子的左儿子就是待翻转的区间所在子树的根,给它打上标记即可
}
初始化
在实际使用过程中,为了防止越界,我们常常会在树中插入一个极小值,一个极大值,本文关于排名的代码都是以已经插入极小值极大值为前提,自己编写程序时一定要记得初始化插入一个极小值,一个极大值
纯享版封装Splay
这里新加入了动态开点功能,可以预先申请空间,也可以在使用时直接插入动态开点,非常方便
code
template<int N=10,typename _Tp=int,long long INF=2147483647> class Splay
{
private:
int Root,node_cnt;
struct Node
{
_Tp v;
int cnt,siz,fa,ch[2];
};
vector<Node> node;
vector<int> del_list;
int vir_alloc()//动态申请点
{
if(!del_list.empty())
{
int tmp=del_list.back();
del_list.pop_back();
return tmp;
}
++node_cnt;
if(node_cnt>=node.size())
{
if(node_cnt==node.capacity()) node.reserve(node.capacity()+15);
node.emplace_back(Node());
}
return node_cnt;
}
void update(int x)//更新
{
node[x].siz=node[node[x].ch[0]].siz+node[node[x].ch[1]].siz+node[x].cnt;
}
void rotate(int x)//旋转
{
int y=node[x].fa,z=node[y].fa,k=(node[y].ch[1]==x);
node[z].ch[node[z].ch[1]==y]=x;
node[x].fa=z;
node[y].ch[k]=node[x].ch[k^1];
node[node[x].ch[k^1]].fa=y;
node[x].ch[k^1]=y;
node[y].fa=x;
update(y),update(x);
}
void splay(int x,int target)//转到目标节点的儿子
{
while(node[x].fa!=target)
{
int y=node[x].fa,z=node[y].fa;
if(z!=target)
((node[z].ch[0]==y)^(node[y].ch[0]==x))?rotate(x):rotate(y);
rotate(x);
}
if(!target)Root=x;
}
void find(_Tp x)//对应值节点转到根
{
int cur=Root;
if(!cur)return;
while(node[cur].ch[x>node[cur].v]&&x!=node[cur].v)
cur=node[cur].ch[x>node[cur].v];
splay(cur,0);
}
public:
Splay()//初始化
{
Root=node_cnt=0;
node.resize(N);
node[0].siz=0,node[0].cnt=0,node[0].fa=0;
insert(INF),insert(-INF);
}
void insert(_Tp x)//插入
{
int cur=Root,from=0;
while(cur&&x!=node[cur].v)
from=cur,cur=node[cur].ch[x>node[cur].v];
if(cur)
++node[cur].cnt;
else
{
cur=vir_alloc();
if(!from) Root=cur;
else node[from].ch[x>node[from].v]=cur;
node[cur].v=x;
node[cur].cnt=1;
node[cur].fa=from;
node[cur].siz=1;
node[cur].ch[0]=node[cur].ch[1]=0;
}
splay(cur,0);
}
int find_pre_id(_Tp x)//查前驱编号
{
find(x);
if(node[Root].v<x)return Root;
int cur=node[Root].ch[0];
while(node[cur].ch[1]) cur=node[cur].ch[1];
return cur;
}
int find_nxt_id(_Tp x)//查后继编号
{
find(x);
if(node[Root].v>x)return Root;
int cur=node[Root].ch[1];
while(node[cur].ch[0]) cur=node[cur].ch[0];
return cur;
}
_Tp find_pre(_Tp x)//查前驱值
{
x=find_pre_id(x);
return node[x].v;
}
_Tp find_nxt(_Tp x)//查后继值
{
x=find_nxt_id(x);
return node[x].v;
}
void erase(_Tp x)//删除
{
int x_pre=find_pre_id(x),x_nxt=find_nxt_id(x);
splay(x_pre,0);
splay(x_nxt,x_pre);
int cur=node[x_nxt].ch[0];
if(node[cur].cnt>1)
{
--node[cur].cnt;
splay(cur,0);
}
else del_list.emplace_back(node[x_nxt].ch[0]),node[x_nxt].ch[0]=0;
}
_Tp kth(int rank)//找排名为k的
{
++rank;
int cur=Root,son;
if(node[cur].siz<rank) return INF;
while(1)
{
son=node[cur].ch[0];
if(rank>node[son].siz+node[cur].cnt)
{
rank-=node[son].siz+node[cur].cnt;
cur=node[cur].ch[1];
}
else if(node[son].siz>=rank) cur=son;
else return node[cur].v;
}
}
int get_rank(_Tp x)//查排名
{
find(x);
if(node[Root].v>=x) return node[node[Root].ch[0]].siz;
return node[node[Root].ch[0]].siz+node[Root].cnt;
}
void reserve(int cap)//直接申请更大空间
{
if(node.capacity()<cap) node.reserve(cap);
}
};
食用方法
将上方代码加入您的代码中,定义时您可以选择性地提供三个可选参数,第一个可选参数 (N) 表示该Splay Tree的节点数预先申请空间,如果节点数超过 (N) 就会自动新申请空间,提供合适的大小能优化您的程序,该参数默认为 (10) 个节点
第二个可选参数 (\_Tp) 表示您在其中所存储值的数据类型,第三个可选参数 (INF) 表示您所希望的正无穷大小,它的类型为long long,如果您不提供可选参数,(\_Tp) 将默认为int,(INF) 将默认为long long类型的 (2147483647)
Splay::reserve(int cap)函数能帮助您在使用过程中直接一次性申请更大的空间
具体见下方栗子
Splay<> A;
//定义一个名为A,初始申请节点空间10个,储值类型为int,正无穷为2147483647的Splay Tree
Splay<19260817> B;
//定义一个名为B,初始申请节点空间19260817个,储值类型为int,正无穷为2147483647的Splay Tree
Splay<500,long long> C;
//定义一个名为C,初始申请节点空间500个,储值类型为long long,正无穷为2147483647的Splay Tree
Splay<114514,double,1919810> D;
//定义一个名为D,初始申请节点空间114514个,储值类型为double,正无穷为1919810的Splay Tree
Splay<123,short int> E[233];
//定义一个名为E的容量为233的一维数组,每一个下标有一个初始申请节点空间123个,储值类型为short int,正无穷为2147483647的Splay Tree
//在(主)函数中
A.reserve(123456);//把名为A的Splay Tree的节点空间扩展到123456
int temp=654321;
A.reserve(temp);//把名为A的Splay Tree的节点空间扩展到654321
致谢
FJN 妹子 和 npy SYQ
该文为本人原创,转载请注明出处