2017ACM暑期多校联合训练

题目链接

Problem Description
Function Fx,ysatisfies:

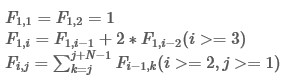
For given integers N and M,calculate Fm,1 modulo 1e9+7.

Input
There is one integer T in the first line.
The next T lines,each line includes two integers N and M .
1<=T<=10000,1<=N,M<2^63.

Output
For each given N and M,print the answer in a single line.

Sample Input
2
2 2

3 3

Sample Output
2
33

分析：
这道题最主要的是找到这一系列数之间的规律，数据范围那么大，肯定是有规律的，奈何比赛的时候找了好久还是没有把规律找对，当时是按照数之间的规律来找的，现在参考题解给出的规律，来看一下具体的解题方法：

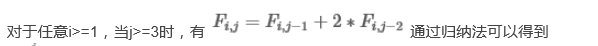
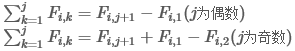
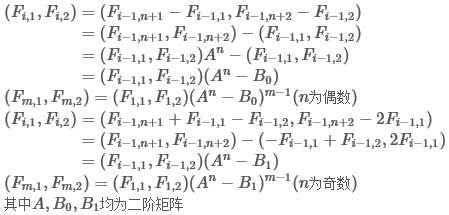
下面具体的要用到矩阵快速幂的方法求解：

首先来推导矩阵A的形式：

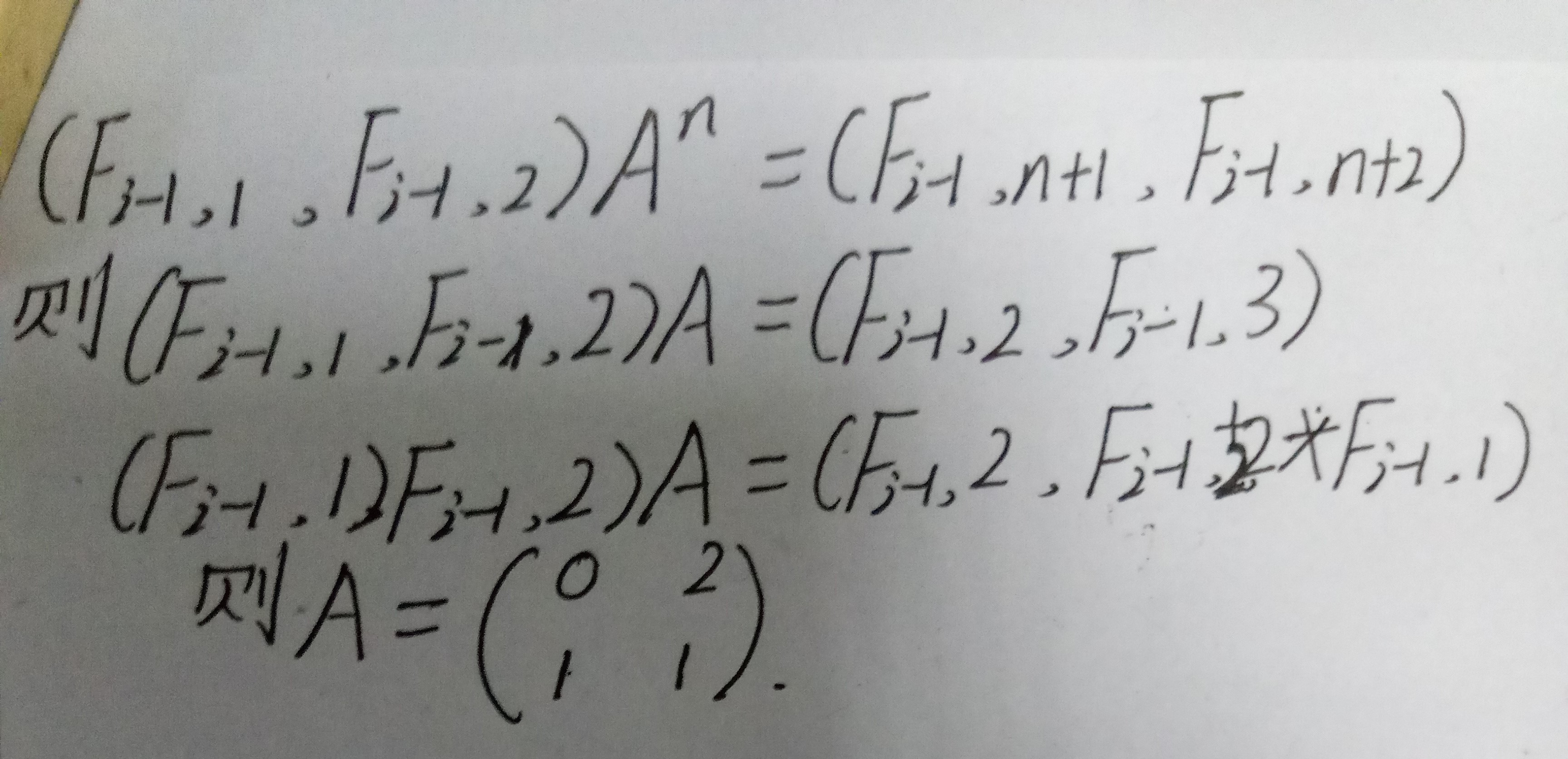
同样的道理，对于矩阵B0，和B1：

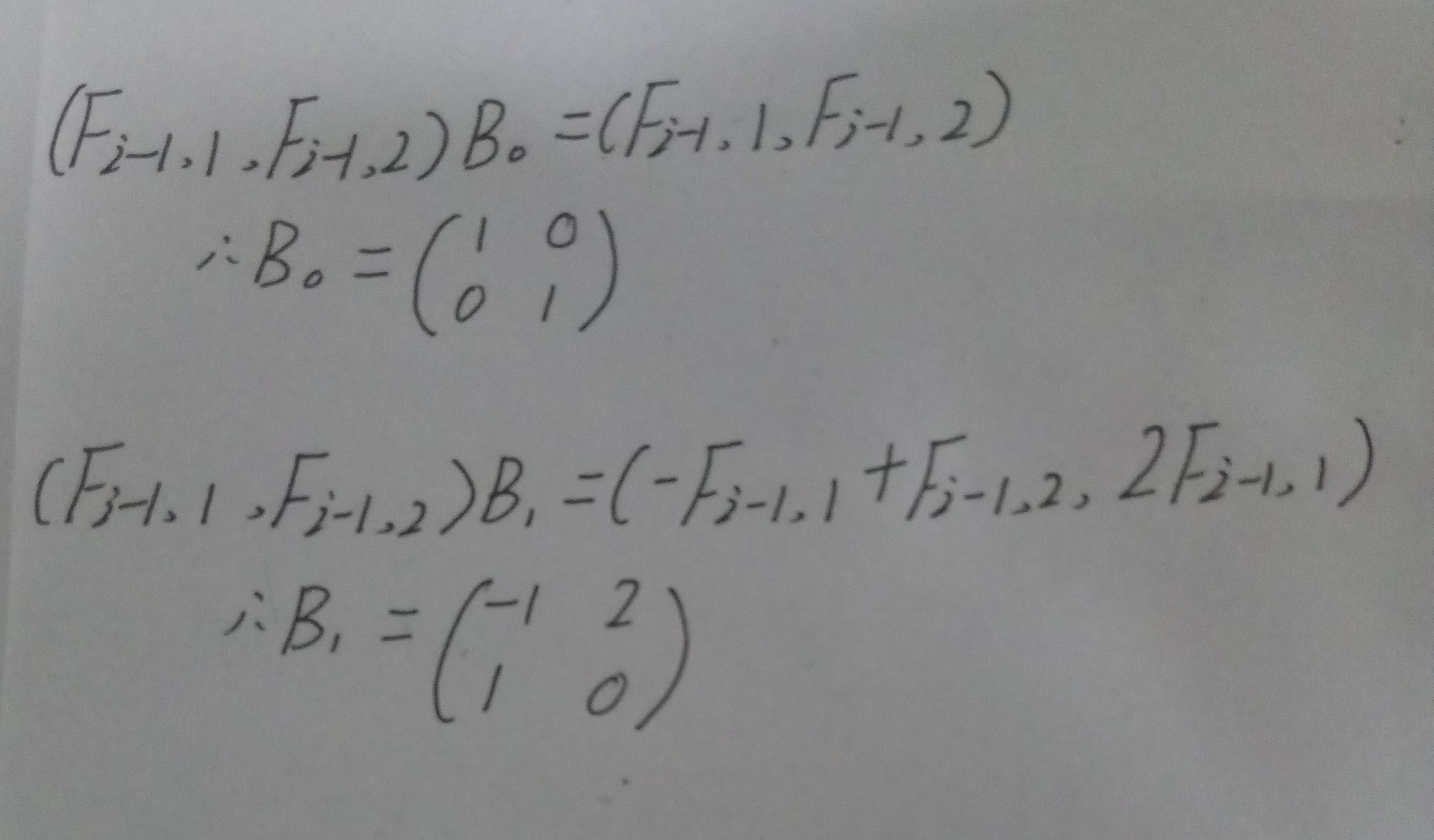
这三个矩阵表示出来以后，就好解决了
矩阵减法就是两个矩阵相应位置上的元素相减，最后需要注意的是Fm,1还是要通过两个矩阵相乘求得的。

矩阵快速幂的算法思想还是很简单的，根整数快速幂思想一样，只是传进去的参数应该是矩阵。

#include <iostream>
#include <cstring>
#include<stdio.h>
using namespace std;
#define SIZE 2

struct matrix
{
    long long e[SIZE][SIZE];
    matrix()
    {
        memset(e, 0, sizeof(e));
    }
} A, A_n;

const long long mod = 1e9+7;      //上限

matrix operator*(matrix &a, matrix &b)///两个矩阵相乘，行上的每个元素对应乘以列上的每个元素然后求和
{
    matrix t;
    for (int i = 0; i < SIZE; ++i)
    {
        for (int j = 0; j < SIZE; ++j)
        {
            for (int k = 0; k < SIZE; ++k)
            {
                t.e[i][j] += a.e[i][k]*b.e[k][j];
                t.e[i][j] %= mod;
            }
        }
    }
    return t;
}

matrix quickpower(matrix &a, long long b)///求矩阵的a的b次方，原理同整数幂一样
{
    matrix ans;
    for (int i = 0; i < SIZE; ++i)
    {
        ans.e[i][i] = 1;
    }
    while (b)
    {
        if (b & 1) ans = ans * a;
        b >>= 1;
        a = a * a;
    }

    return ans;
}

int main(int argc, char const *argv[])
{
    int testn;
    scanf("%d", &testn);

    while (testn--)
    {
        long long n, m;
        scanf("%I64d %I64d", &n, &m);
        ///矩阵A
        A.e[0][0] = 0;
        A.e[1][0] = A.e[1][1] = 1;
        A.e[0][1] = 2;
        ///求得矩阵An
        A_n = quickpower(A, n);

        matrix b;
        if(n & 1)
        {
            ///矩阵B1
            b.e[0][0] = -1;
            b.e[0][1] = 2;
            b.e[1][0] = 1;
            b.e[1][1] = 0;
        }
        else
        {
            ///矩阵B0
            b.e[0][0] = b.e[1][1] = 1;
            b.e[0][1] = b.e[1][0] = 0;
        }
        ///矩阵An-B0（B1）
        A_n.e[0][0] -= b.e[0][0];
        A_n.e[0][1] -= b.e[0][1];
        A_n.e[1][0] -= b.e[1][0];
        A_n.e[1][1] -= b.e[1][1];

        A_n = quickpower(A_n, m-1);

        long long ans = (A_n.e[0][0] + A_n.e[1][0]) % mod;
        printf("%I64d
", ans);
    }
    return 0;
}

这是题解里面给出的解题思路，其实自己根据观察第一列的元素也是可以总结出来规律的，这里就给个同学总结的完整版的讲解。
先将其一系列的数据打表：

C++n=2                         
1   1   3   5   11  21  43   85
2   4   8   16  32  64  128  256
6   12  24  48  96  192 384  768
18  36  72  144 288 576 1152 2304
n=3                         
1   1   3   5    11   21    43    85
5   9   19  37   75   149   299   597
33  65  131 261  523  1045  2091  4181
229 457 915 1829 3659 7317  14635 29269
n=4                         
1    1    3    5     11    21    43     85
10   20   40   80    160   320   640    1280
150  300  600  1200  2400  4800  9600   19200
2250 4500 9000 18000 36000 72000 144000 288000
n=5                         
1      1       3       5       11      21       43       85
21     41      83      165     331     661      1323     2645
641    1281    2563    5125    10251   20501    41003    82005
19861  39721   79443   158885  317771  635541   1271083  2542165
615681 1231361 2462723 4925445 9850891 19701781 39403563 78807125

要求的是F(m,1)，则肯定与上面的结果有关系的，数据量过大，肯定是没有办法循环得到结果，由此看出，这道题必是规律题。

当n为奇数和偶数的时候，求F(m,1)的规律是不一样的。

偶数： 打表可以看出当n为偶数的时候，从F(2,1)开始，第一列的下一个是上一个的k倍，多打机组数据可看出，k为3,15,63,255……k的规律就是2^n-1。由此可得出，当n为偶数的时候，F(m,1) = F(2,1)×(2^n-1)^(m-2)。
奇数： 奇数求解的过程就相对来说比较复杂一点了。当n为奇数的时候，可以发现，F(m-1,1)×(2^n-1)与F(m,1)之间为一个常数k。我们就可以进一步的通过这样的关系求出F(m,1)的值
奇数求解过程：通过打表可以看出，当n等于3,5,7,9……的时候，k的值为2,10,42,170……
可以看出之间的规律：

2 = 2^1
10 = 2^1+2^3
42 = 2^1+2^3+2^5
170 = 2^1+2^3+2^5+2^7
……
//可以看出是等比为2^2的前k项和  

结合上面可以得出：F(m-1,1)(2^n-1)-F(m,1) = Sk
F(m,1) = F(m-1,1)(2^n-1)-Sk;
又可以根据这个公式推出

算到这里就仅仅剩下F(2,1)的求解了
先打表看看n:(1~i)第一行与F（2,1）的关系

C++S[i]: 1 1 3 5 11 21 43 85 171 341 683 1365 2731 5461 10923 21845 43691 87381 174763 349525
F[i]: 1 2 5 10 21 42 85 170 341 682 1365 2730 5461 10922 21845 43690 87381 174762 349525

123 S[i]: 1 1 3 5 11 21 43 85 171 341 683 1365 2731 5461 10923 21845 43691 87381 174763 349525F[i]: 1 2 5 10 21 42 85 170 341 682 1365 2730 5461 10922 21845 43690 87381 174762 349525  

F[i]表示当n为i时F(2,1)的值。
当i为奇数的时候F[i]=s[i+1];当i为偶数的时候F[i]=s[i+1]-1;
s[i+1]=((-1)^i+2^(i+1))/3;
接下来的求解过程就只需要注意边计算边取模就可以了。

注意：在对除数取余的时候为了防止精度的丢失，需要用到乘法的逆元，将除法变成乘法。这里使用的乘法逆元算法为费马小定理。

费马小定理
在p是素数的情况下，对任意整数x都有x^p≡x(mod)p。
可以在p为素数的情况下求出一个数的逆元，x∗x^(p−2)≡1(mod p)，x^(p−2)即为逆元。

ll mult(ll a,ll n)  //求a^n%mod
{
    ll s=1;
    while(n)
    {
        if(n&1)s=s*a%mod;
        a=a*a%mod;
        n>>=1;
    }
    return s;
} //mult(a,n-2);

代码实现：

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <vector>
#include<iostream>
using namespace std;

typedef __int64 LL;
const int mod = 1e9+7;
LL n,m;
LL mult(LL a,LL n)
{
    LL ans=1;
    while(n)
    {
        if(n&1)ans=(ans*a)%mod;
        a=(a*a)%mod;
        n>>=1;
    }
    return ans;
}

void solve()
{
    if(m==1)
    {
        cout<<"1"<<endl;
        return;
    }
    LL three=mult(3,mod-2);         // 3 的逆元 费马小定理 求乘法逆元
    LL one=((mult(2,n+1)+(n&1?-1:1)+mod)%mod*three)%mod;    // F[1][n+1]
    if(n%2==0)
        one=(one-1+mod)%mod;  // 计算 F[2][1]
    LL ans=0;
    LL mu=(mult(2,n)-1+mod)%mod;    // 2^n-1
    LL mun=mult(mu,m-2);            // (2^n-1)^(m-2)
    if(n%2==0)                      // 偶数时
        ans=(one*mun)%mod;
    else                            // 奇数时
    {
        LL cha=n/2;
        cha=((2*(mult(4,cha)-1+mod)%mod)%mod)*three%mod;
        LL add=((cha*(mun-1+mod)%mod)*mult((mu-1+mod)%mod,mod-2))%mod;
        ans=((one*mun)%mod-add+mod)%mod;
    }
    cout<<ans<<endl;
}

int main()
{
    ios::sync_with_stdio(false);
    int T;
    cin>>T;
    while(T--)
    {
        cin>>n>>m;
        solve();
    }
    return 0;
}