首先是题目链接 http://codevs.cn/problem/1922/
结果发现题目没图(心情复杂
然后去网上扒了一张图
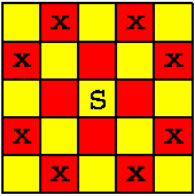
大概就是这样了。
如果把每个点和它可以攻击的点连一条边,那问题就变成了求二分图的最大独立集了 (二分图最大独立集:即一个点集,集合中任两个结点不相邻),然后就是建图了。
题图非常好心的帮忙染色了,所以我们可以看出来,一个点可以到达的点和它的颜色是不一样的,所以只需要黑白染色就可以了,然后把黑点看作一个集合, 白点看作一个集合,又因为二分图最大独立集=顶点总数 - 最大匹配,而后我们就只需要求最大匹配就可以了。
最大匹配最经典的就是匈牙利啦,但是网络流也可以做, 而且dinic在边容量为一的时候跑得特别快,所以就用dinic了(顺便练习一下dinic233
建图方法:超级源S连接所有的黑点,且边的容量为1, 黑点连接它所有能攻击到的白点,边的容量为INF, 然后所有的白点再连接超级汇T, 容量仍然是为1。跑一遍dinic就可以了(建图的正确性可以自己画图证明
1 #include <cstdio> 2 #include <vector> 3 #include <cstring> 4 #include <algorithm> 5 #include <queue> 6 #include <iostream> 7 using namespace std; 8 const int N = 210; 9 10 int n, m, cnt, w; 11 12 struct Edge{ 13 int from, to, cap, flow; 14 }; 15 vector < int > G[N*N]; 16 vector < Edge > edge; 17 bool vis[N*N]; 18 int s, t, d[N*N], cur[N*N], INF = (1<<30), flag[N][N]; 19 int py[8][2] = {{2, 1}, {2, -1}, {-2, 1}, {-2, -1}, {1, 2}, {1, -2}, {-1, 2}, {-1, -2}}; 20 21 inline void read(int &ans){ 22 static char buf = getchar(); 23 register int neg = 1; 24 ans = 0; 25 for (;!isdigit(buf); buf = getchar()) 26 if (buf == '-') neg = -1; 27 for (;isdigit(buf); buf = getchar()) 28 ans = ans*10 + buf - '0'; 29 ans *= neg; 30 } 31 32 inline void Add(int from, int to, int cap){ 33 edge.push_back((Edge){from, to, cap, 0}); 34 edge.push_back((Edge){to, from, 0, 0}); 35 int m = edge.size(); 36 G[from].push_back(m - 2); 37 G[to].push_back(m - 1); 38 } 39 40 bool ok(int x, int y){ 41 if (x > 0 && x <= n && y > 0 && y <= n) 42 if (flag[x][y] != -1) 43 return true; 44 return false; 45 } 46 47 inline void build(){ 48 for (int i = 1; i <= n; i++) 49 for (int j = 1; j <= n; j++) 50 if (flag[i][j] == -1) continue; 51 else if (flag[i][j] < cnt){ 52 for (int k = 0; k < 8; k++){ 53 int x = i + py[k][0]; 54 int y = j + py[k][1]; 55 if (ok(x, y)) 56 Add(flag[i][j], flag[x][y], INF); 57 } 58 Add(0, flag[i][j], 1); 59 } 60 else Add(flag[i][j], w, 1); 61 } 62 63 inline bool BFS(){ 64 memset(vis, 0, sizeof(vis)); 65 memset(d, 0xff, sizeof(d)); 66 queue < int > q; 67 q.push(s); 68 d[s] = 0; 69 vis[s] = 1; 70 while(!q.empty()){ 71 int u = q.front(); q.pop(); 72 for (int i = 0; i < G[u].size(); i++){ 73 Edge& e = edge[G[u][i]]; 74 if (!vis[e.to] && e.cap > e.flow){ 75 d[e.to] = d[u] + 1; 76 vis[e.to] = 1; 77 q.push(e.to); 78 } 79 } 80 } 81 return vis[t]; 82 } 83 84 int dfs(int x, int a){ 85 if (x == t || a == 0) return a; 86 int flow = 0, f; 87 for (int& i = cur[x]; i < G[x].size(); i++){ 88 Edge& e = edge[G[x][i]]; 89 if (d[x] + 1 == d[e.to] && (f = dfs(e.to, min(e.cap - e.flow, a))) > 0){ 90 e.flow += f; 91 edge[G[x][i]^1].flow -= f; 92 flow += f; 93 a -= f; 94 if (a == 0) break; 95 } 96 } 97 return flow; 98 } 99 100 inline int dinic(){ 101 int ans = 0; 102 while(BFS()){ 103 memset(cur, 0, sizeof(cur)); 104 ans += dfs(0, INF); 105 } 106 return ans; 107 } 108 109 int main(){ 110 read(n); read(m); 111 for (int i = 0; i < m; i++){ 112 int x, y; 113 read(x); read(y); 114 flag[x][y] = -1; 115 } 116 cnt = 1; 117 w = (n * n + 1)/2 + 1; 118 for (int i = 1; i <= n; i++) 119 for (int j = 1; j <= n; j++) 120 if ((i + j)%2 == 0){ 121 if (flag[i][j] != -1) flag[i][j] = cnt; 122 cnt++; 123 } 124 else{ 125 if (flag[i][j] != -1) flag[i][j] = w; 126 w++; 127 } 128 s = 0, t = n*n + 1; 129 build(); 130 printf("%d", n*n - m - dinic()); 131 return 0; 132 }
然而这道题最开始写的时候TLE了
然后就加了当前弧优化
然后就A了(滑稽
但是可以看得出来非常的慢
测试点#kni0.in 结果: 内存使用量: 1512kB 时间使用量: 1ms
测试点#kni1.in 结果: 内存使用量: 1388kB 时间使用量: 1ms
测试点#kni10.in 结果: 内存使用量: 7256kB 时间使用量: 415ms
测试点#kni2.in 结果: 内存使用量: 1516kB 时间使用量: 1ms
测试点#kni3.in 结果: 内存使用量: 1644kB 时间使用量: 1ms
测试点#kni4.in 结果: 内存使用量: 1772kB 时间使用量: 3ms
测试点#kni5.in 结果: 内存使用量: 1772kB 时间使用量: 4ms
测试点#kni6.in 结果: 内存使用量: 1768kB 时间使用量: 2ms
测试点#kni7.in 结果: 内存使用量: 2020kB 时间使用量: 4ms
测试点#kni8.in 结果: 内存使用量: 4444kB 时间使用量: 143ms
测试点#kni9.in 结果: 内存使用量: 11732kB 时间使用量: 927ms
然后上网搜了一下其他的题解,发现其他的代码都跑得很快,然后就把建图方式改了一下
1 #include <cstdio> 2 #include <vector> 3 #include <cstring> 4 #include <algorithm> 5 #include <queue> 6 #include <iostream> 7 using namespace std; 8 const int N = 210; 9 10 int n, m, cnt, w; 11 12 struct Edge{ 13 int from, to, cap, flow; 14 }; 15 vector < int > G[N*N]; 16 vector < Edge > edge; 17 bool vis[N*N]; 18 int s, t, d[N*N], cur[N*N], INF = (1<<30), flag[N][N], b[N*N]; 19 int py[8][2] = {{2, 1}, {2, -1}, {-2, 1}, {-2, -1}, {1, 2}, {1, -2}, {-1, 2}, {-1, -2}}; 20 21 inline void read(int &ans){ 22 static char buf = getchar(); 23 register int neg = 1; 24 ans = 0; 25 for (;!isdigit(buf); buf = getchar()) 26 if (buf == '-') neg = -1; 27 for (;isdigit(buf); buf = getchar()) 28 ans = ans*10 + buf - '0'; 29 ans *= neg; 30 } 31 32 inline void Add(int from, int to, int cap){ 33 edge.push_back((Edge){from, to, cap, 0}); 34 edge.push_back((Edge){to, from, 0, 0}); 35 int m = edge.size(); 36 G[from].push_back(m - 2); 37 G[to].push_back(m - 1); 38 } 39 40 bool ok(int x, int y){ 41 if (x > 0 && x <= n && y > 0 && y <= n) 42 if (flag[x][y] != -1) 43 return true; 44 return false; 45 } 46 47 inline int hash(int i,int j){ 48 return (i - 1)*n + j; 49 } 50 51 inline bool BFS(){ 52 memset(vis, 0, sizeof(vis)); 53 memset(d, 0xff, sizeof(d)); 54 queue < int > q; 55 q.push(s); 56 d[s] = 0; 57 vis[s] = 1; 58 while(!q.empty()){ 59 int u = q.front(); q.pop(); 60 for (int i = 0; i < G[u].size(); i++){ 61 Edge& e = edge[G[u][i]]; 62 if (!vis[e.to] && e.cap > e.flow){ 63 d[e.to] = d[u] + 1; 64 vis[e.to] = 1; 65 q.push(e.to); 66 } 67 } 68 } 69 return vis[t]; 70 } 71 72 int dfs(int x, int a){ 73 if (x == t || a == 0) return a; 74 int flow = 0, f; 75 for (int& i = cur[x]; i < G[x].size(); i++){ 76 Edge& e = edge[G[x][i]]; 77 if (d[x] + 1 == d[e.to] && (f = dfs(e.to, min(e.cap - e.flow, a))) > 0){ 78 e.flow += f; 79 edge[G[x][i]^1].flow -= f; 80 flow += f; 81 a -= f; 82 if (a == 0) break; 83 } 84 } 85 return flow; 86 } 87 88 inline int dinic(){ 89 int ans = 0; 90 while(BFS()){ 91 memset(cur, 0, sizeof(cur)); 92 ans += dfs(0, INF); 93 } 94 return ans; 95 } 96 97 int main(){ 98 read(n); read(m); 99 for (int i = 0; i < m; i++){ 100 int x, y; 101 read(x); read(y); 102 b[hash(x, y)] = 1; 103 } 104 cnt = 1; 105 s = 0, t = n*n + 1; 106 for(int i = 1; i <= n;i++) 107 for(int j = 1; j <=n; j++){ 108 if(!b[hash(i,j)] && ((i+j)&1)){ 109 Add(s, hash(i,j), 1); 110 if(i > 2 && j > 1 && !b[hash(i-2,j-1)]) 111 Add(hash(i,j), hash(i-2,j-1), INF); 112 if(i > 2 && j + 1 <= n && !b[hash(i-2,j+1)]) 113 Add(hash(i,j), hash(i-2,j+1), INF); 114 if(i > 1 && j > 2 && !b[hash(i-1,j-2)]) 115 Add(hash(i,j), hash(i-1,j-2), INF); 116 if(i > 1 && j + 2 <= n &&!b[hash(i-1,j+2)]) 117 Add(hash(i,j), hash(i-1,j+2), INF); 118 if(i + 2 <= n && j > 1 && !b[hash(i+2,j-1)]) 119 Add(hash(i,j), hash(i+2,j-1), INF); 120 if(i + 2 <= n && j + 1 <= n && !b[hash(i+2,j+1)]) 121 Add(hash(i,j), hash(i+2,j+1), INF); 122 if(i + 1 <= n && j > 2 && !b[hash(i+1,j-2)]) 123 Add(hash(i,j), hash(i+1,j-2), INF); 124 if(i + 1 <= n && j + 2 <= n && !b[hash(i+1,j+2)]) 125 Add(hash(i,j), hash(i+1,j+2), INF); 126 } 127 if(!b[hash(i,j)] && !((i+j)&1)) Add(hash(i,j), t, 1); 128 } 129 130 printf("%d", n*n - m - dinic()); 131 return 0; 132 133 }
修改之后
测试点#kni0.in 结果: 内存使用量: 1640kB 时间使用量: 2ms
测试点#kni1.in 结果: 内存使用量: 1512kB 时间使用量: 2ms
测试点#kni10.in 结果: 内存使用量: 7256kB 时间使用量: 178ms
测试点#kni2.in 结果: 内存使用量: 1512kB 时间使用量: 2ms
测试点#kni3.in 结果: 内存使用量: 1640kB 时间使用量: 2ms
测试点#kni4.in 结果: 内存使用量: 1772kB 时间使用量: 2ms
测试点#kni5.in 结果: 内存使用量: 1772kB 时间使用量: 2ms
测试点#kni6.in 结果: 内存使用量: 1772kB 时间使用量: 2ms
测试点#kni7.in 结果: 内存使用量: 2020kB 时间使用量: 4ms
测试点#kni8.in 结果: 内存使用量: 4568kB 时间使用量: 92ms
测试点#kni9.in 结果: 内存使用量: 11608kB 时间使用量: 52ms
少了一个二维循环 + 减少了常数
结果快了1200ms(一脸懵逼