- 1 将 0.1 累加 100 次也得不到 10
- 2 用二进制数表示小数
- 3 计算机运算出错的原因
- 4 什么是浮点数
- 5 正则表达式和 EXCESS 系统
- 6 在实际的程序中进行确认
- 7 如何避免计算机计算出错
- 8 二进制数和十六进制数
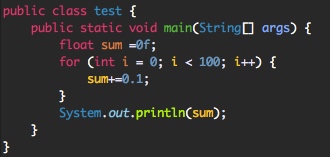
1 将 0.1 累加 100 次也得不到 10
将 0.1 累加 100 次,然后将结果输出到显示器上

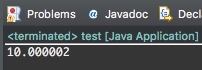 

2 用二进制数表示小数
在说明计算机如何用二进制数表示小数的具体方法前,我们先做 个热身,把 1011.0011 这个有小数点的二进制数转换成十进制数。

3 计算机运算出错的原因
计算 机之所以会出现运算错误,是因为“有一些十进制数的小数无法转换成 二进制数”。
例如,十进制数 0.1,就无法用二进制数正确表示,小数 点后面即使有几百位也无法表示。图 3-2 中, 小 数 点 后 4 位 用 二 进 制 数 表 示 时 的 数 值 范 围 为 0.0000~0.1111。因此,这里只能表示 0.5、0.25、0.125、0.0625 这四个 二进制数小数点后面的位权组合而成(相加总和)的小数。将这些数值 组合后能够表示的数值,即为表 3-1 中所示的无序的十进制数。

十进制数 0 的下一位是 0.0625。因此,这中间的小数, 就无法用小数点后 4 位数的二进制数来表示。
4 什么是浮点数
像 1011.0011 这样带小数点的表现形式,完全是纸面上的二进制数 表现形式,在计算机内部是无法使用的。
很多编程语言中都提供了两种表示小数的数据类型,分别是双精 度浮点数和单精度浮点数。 双精度浮点数类型用 64 位、 单精度浮点数类型用 32 位来表示全体小数。
浮点数是指用符号、尾数、基数和指数这四部分来表示的小数
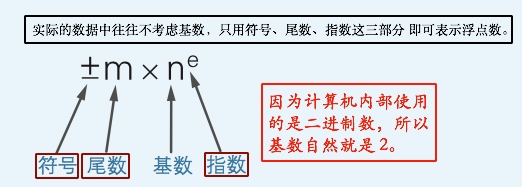 

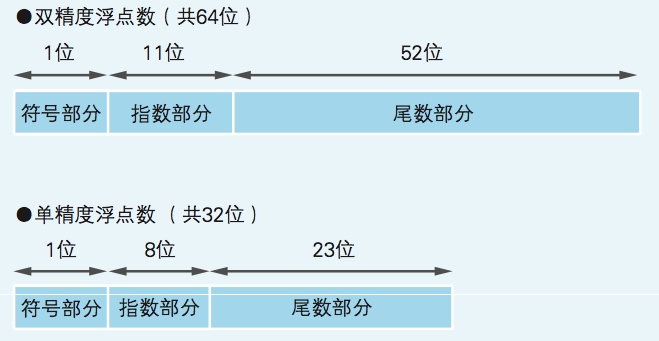 

符号部分是指使用一个数据位来表示数值的符号。该数据位是 1 时表示负,为 0 时则表示“正或者 0”。尾数部分用的是“将小数点前面 的值固定为 1 的正则表达式”.指数部分用的则是“EXCESS 系统表现”。
5 正则表达式和 EXCESS 系统
5.1 位数部分
尾数部分使用 正则表达式,可以将表现形式多样的浮点数统一为 一种表现形式。
例如,十进制数 0.75 就有很多种表现形式

因此,为了方便计算机处理,需要制定一个 统一的规则。
例如,十进制数的浮点数应该遵循“小数点前面是 0,小 数点后面第 1 位不能是 0”这样的规则。
我们使用的是“将小数点前面的值固定为1的正则表达式”。具体来讲,就是将二进制数表示的小数左移或右移(这里是逻辑移位。因为符号位是独立的B)数次后,整数部分的第1位变为1,第2位之后都变为 0(这样是为了消除第 2 位以上的数位)。而且,第 1 位的 1 在实际的数据中不保存。由于第 1 位必须是 1,因此,省略该部分后就 节省了一个数据位,从而也就可以表示更多的数据范围(虽不算太多)。
单精度浮 点数中,尾数部分是 23 位,但由于第 1 位的 1 被省略了,所以实际上 可以表示 24 位的数值。

5.2 指数部分
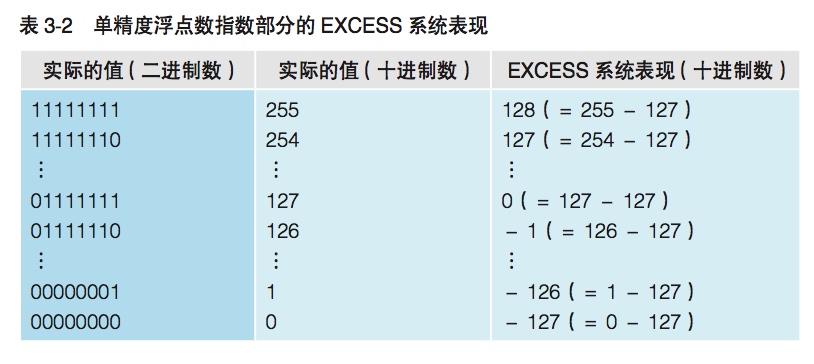
指数部分中使用的 EXCESS 系统, 使用这种方法主要是为了表示负数时不使用符号位。
EXCESS 系统表现是指,通过将指数部分表示范围的中间值设为 0,使得负数不 需要用符号来表示。也就是说,当指数部分是 8 位单精度浮点数时, 最大值 11111111 = 255 的 1/2,即 01111111 = 127(小数部分舍弃)表示 的是 0,指数部分是 11 位双精度浮点数时,11111111111 = 2047 的 1/2, 即 01111111111 = 1023(小数部分舍弃)表示的是 0。
EXCESS 系统可能不太好理解,下面举例来说明。假设有这样一 个游戏,用1~13(A~K)的扑克牌来表示负数。这时,我们可以把中间的 7 这张牌当成 0。如果扑克牌 7 是 0,10 就表示+3,3 就表 示-4。事实上,这个规则说的就是 EXCESS 系统。

6 在实际的程序中进行确认
如 何用单精度浮点数来表示十进制数 0.75 吧。
用于确认单精度浮点数表示方法的 C 语言程序
#include <stdio.h>
#include <string.h>
void main() {
float data;
unsigned long buff;
int i;
char s[34];
// 将 0.75 以单精度浮点数的形式存储在变量 date 中。
data = (float)0.75;
// 把数据复制到 4 字节长度的整数变量 buff 中以逐个提取出每一位。
memcpy(&buff, &data, 4);
// 逐一提取出每一位
for (i = 33; i >= 0; i--) {
if(i == 1 || i == 10) {
// 加入破折号来区分符号部分、指数部分和尾数部分。
s[i] = '-';
} else {
// 为各个字节赋值 '0' 或者 '1'。
if (buff % 2 == 1) {
s[i] = '1';
} else {
s[i] = '0';
}
buff /= 2;
}
}
s[34] = '�';
// 显示结果。
printf("%s
", s);
}
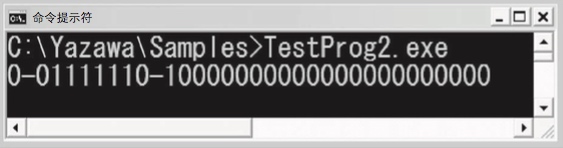 

该程序执行后,十进制数 0.75 用单精度浮点数来表示就变成了 0-01111110-10000000000000000000000。加入破折号(-)是为 了区分符号部分、指数部分、尾数部分。这里,符号部分为 0,指数部分为 01111110,尾数部分为 10000000000000000000000。
- 因为 0.75 是 正数,所以符号位是 0。
- 指数部分的 01111110 是十进制数 126,用 EXCESS 系统表现就是-1(126-127 = -1)。
- 根据正则表达式的规则, 小数点前面的第 1 位是 1,因此尾数部分10000000000000000000000 实 际上表示的是 1.10000000000000000000000 这个二进制数。将尾数部分 的二进制数转换成十进制数,结果就是(1 ×2 的 0 次幂)+(1 ×2 的-1次幂)= 1.5。
因此,0-01111110-10000000000000000000000 这个单精度 浮点数,表示的就是“+ 1.5 ×2 的-1 次幂”。2 的-1 次幂是 0.5,+ 1.5 × 0.5 = + 0.75。正好吻合,结果正确。
 

接下来,我们继续使用该程序来看一下如何用单精度浮点数表示十进 制数 0.1。运行后就会发现结果为 0-01111011-10011001100110011001101
(只需将 data = (float)0.75; 的部分变成 data = (float)0.1; 即可)。这时, 如果反过来计算一下这个数值的十进制数,估计大家又要冒汗了,结 果居然不是 0.1。
7 如何避免计算机计算出错
- 首先是回避策略,即无视这些错误。
- 另一个策略是把小数转换成整数来计算。
例如,本章一开头讲过的将 0.1 相 加 100 次这一计算,就可以转换为将 0.1 扩大 10 倍后再将 1 相加 100 次的计算,最后把结果除以 10 就可以了(代码清单 3-3)。
8 二进制数和十六进制数
8.1 整数情况
在以位为单 位表示数据时,使用二进制数很方便,但如果位数太多,看起来就比 较麻烦。因此,在实际程序中,也经常会用十六进制数来代替二进制数。
二进制数的 4 位,正好相当于十六进制数的 1 位。
例如,32 位二 进制数 00111101110011001100110011001101 用十六进制数来表示的话,就是 3DCCCCCD 这个 8 位数。由此可见,通过使用十六进制数,二进 制数的位数能够缩短至原来的 1/4。位数变少之后,看起来也就更清晰 了(图 3-9)。

8.2 小数情况
用十六进制数来表示二进制小数时,小数点后的二进制数的 4 位 也同样相当于十六进制数的 1 位。不够 4 位时用 0 填补二进制数的低 位即可。
例如,1011.011 的低位补 0 后为 1011.0110,这时就可以表示 为十六进制数 B.6(图 3-10)。十六进制数的小数点后第 1 位的位权是 16-1,即 1/16 = 0.0625,这个大家应该能理解吧。