君若不娶,雪离不嫁,君若身亡,众生陪葬。
算法分析
1.RC4是一个典型的基于非线性数组变换的序列密码。它以一个足够大的数组S为基础,对其进行非线性变换,产生非线性的密钥流序列。
2.RC4算法S盒的大小根据参数n的值而变化,通常n=8,这样RC4可生成256个元素的数组S。
3.种子密钥长度为1~ 256个字节(8~2048比特)的可变长度,用于初始化256个字节的初始向量S。
4.RC4有两个主要算法:
- 密钥调度算法(KSA):用于打乱S盒的初始排列。
- 伪随机数生成算法(PRGA):用于输出随机序列并修改S的当前排列。
5.具体过程如下:
- 首先初始化S 即
S[i] = i同时建立数组T用于填充秘钥K(若len(K)<256, 则按序反复填充,直到T被填满) - 然后,对于每个S[i],根据T[i]的值将S[i] 与S中的另一个字节对换。
- 最后,利用PRGA生成秘钥流。从S中随机选取一个元素输出,并置换S以便下一次选取,选取过程取决于索引
i,j。 - 加密时,K的值与明文字节异或;解密时,K的值与密文异或。
算法实现
# KSA 初始化S盒
def InitSbox(k):
# 初始化S盒 存初始值0-255
S = list(range(256))
T = [] # 用于轮转存放key
for i in range(256):
T.append(ord(k[i % len(k)])) # 存放轮转的256位key
j = 0
for i in range(256):
j = (j + S[i] + T[i]) % 256
# 通过交换,打乱S盒
S[i], S[j] = S[j], S[i]
return S
# PRGA生成密钥流
def encrypt(m, k):
c = ""
i = j = 0
# 调用已经初始化的S盒
S = InitSbox(k)
for x in range(len(m)):
i = (i + 1) % 256
j = (j + S[i]) % 256
S[i], S[j] = S[j], S[i] # 交换 打乱S盒
t = (S[i] + S[j]) % 256
# 将生成的密钥流key逐一与明文进行异或,格式化成16进制字符串
c += '%02x' % (ord(m[x]) ^ S[t])
return c
if __name__ == "__main__":
# 加密
m = "ifnottothesunforsmilingwarmisstillinthesuntherebutwewilllaughmoreconfidentcalmifturnedtofoundhisownshadowappropriateescapethesunwillbethroughtheheartwarmeachplacebehindthecornerifanoutstretchedpalmcannotfallbutterflythenclenchedwavingarmsgivenpowerificanthavebrightsmileitwillfacetothesunshineandsunshinesmiletogetherinfullbloom"
k = "qwertyuiop"
ans = encrypt(m, k)
print("加密后得到的内容为: \n" + ans)
# 解密
c = ans #获取密文
b = ""
text = ""
# 将16进制字符串转换为相应字符,存入字符串b中
for i in range(0, len(c), 2):
b += str(chr(int(c[i : i + 2], 16)))
# 解密其实就是再次与密钥流进行异或,再次调用encrypt函数
res = encrypt(b, k)
# 异或后的16进制对应相应的明文字符,转换为相应字符
for i in range(0, len(res), 2):
text += str(chr(int(res[i : i + 2], 16)))
print("解密后得到的明文为: \n" + text)
加密与解密
加密与解密使用同一个加密函数,因为解密其实就是再次与密钥流进行异或。结果如下。
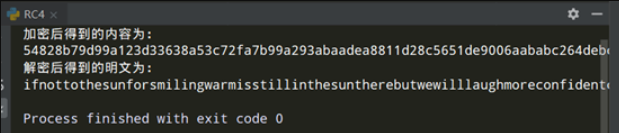
正确性
算法主要包含密钥调度算法(KSA):用于打乱S盒的初始排列 和伪随机数生成算法(PRGA)用于输出随机序列并修改S的当前排列。前者的所有操作仅仅是改变位置。后者的秘钥序列生成过程较为复杂(很好地打乱),但加解密使用的是同一个秘钥K,故随机生成后的秘钥序列依然是相同的,加上加解密只是简单的异或运算,故算法正确。
安全性分析
1.由算法的实现可知,RC4算法的加解密对种子秘钥的依赖十分强烈。故需要保证种子秘钥的安全性。对于此,可进行相关攻击。
- 可以进行穷举搜素攻击,故为了保证安全强度,目前要求秘钥长度至少为128位。
- 弱密钥攻击,弱密钥会产生重复的密钥流,一旦子密钥序列出现了重复,密文就有可能被破解。
2.算法存在无效的初始置换,j = (j + S[i] + T[i]) mod 256 取 (j+T[i])mod 256 ≡ 0 即T[i]=[0,0,255,254,253,...,2] 这样的情况下,S盒完全不会被搅乱,都是无效替换。这样便可以通过统计分析破解。