归纳总结
这个表格总结了各种排序算法的复杂度与稳定性:
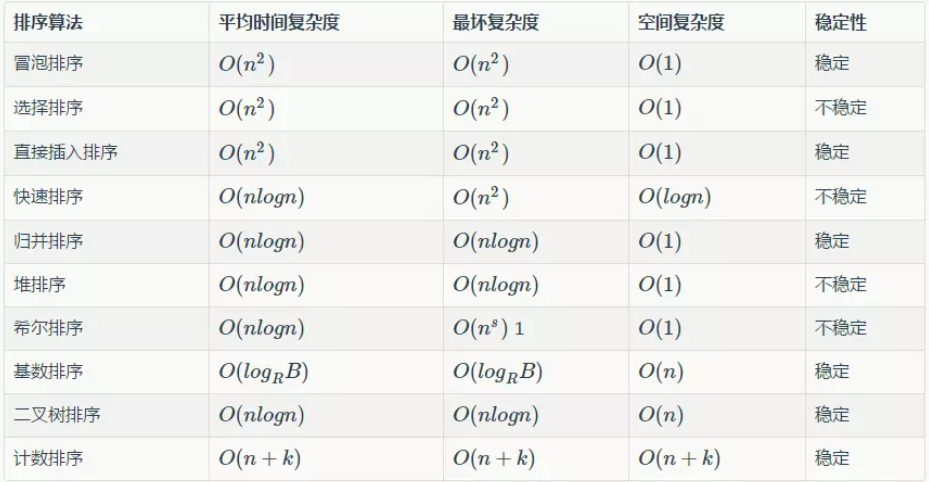
下面是关于相关排序的代码实现。
冒泡排序
#include <iostream>
using namespace std;
void bubbleSort(int a[], int len)
{
int i, j, t;
//将最小的先放到第一个位置
for (i = 0; i < len - 1; i++)
{
for (j = len - 1; j > i; j--)
{
if (a[j] < a[j - 1])
{
t = a[j];
a[j] = a[j - 1];
a[j - 1] = t;
}
}
}
//将最大的先放到最后一个位置
/*for (i = 0; i < len - 1; i++)
{
for (j = 0; j <len - 1 - i; j++)
{
if (a[j] > a[j + 1])
{
t = a[j];
a[j] = a[j + 1];
a[j + 1] = t;
}
}
}*/
}
int main()
{
int array[] = { 34, 65, 12, 43, 67, 5, 78, 10, 3, 70 }, k;
int len = sizeof(array) / sizeof(int);
cout << "The orginal array are:" << endl;
for (k = 0; k < len; k++)
cout << array[k] << ",";
cout << endl;
bubbleSort(array, len);
cout << "The sorted array are:" << endl;
for (k = 0; k < len; k++)
cout << array[k] << ",";
cout << endl;
system("pause");
return 0;
}
选择排序
#include <iostream>
using namespace std;
void selectSort(int a[], int len)
{
int i, j, k, tem;
for (i = 0; i < len - 1; i++)
{
k = i;
for (j = k + 1; j < len; j++)
{
if (a[k] > a[j])
{
k = j;
}
}
if (i != k)
{
tem = a[i];
a[i] = a[k];
a[k] = tem;
}
}
}
int main()
{
int array[] = { 34, 65, 12, 43, 67, 5, 78, 10, 3, 70 }, k;
int len = sizeof(array) / sizeof(int);
cout << "The orginal array are:" << endl;
for (k = 0; k < len; k++)
cout << array[k] << ",";
cout << endl;
selectSort(array, len);
cout << "The sorted array are:" << endl;
for (k = 0; k < len; k++)
cout << array[k] << ",";
cout << endl;
system("pause");
return 0;
}
插入排序
#include <iostream>
//直接插入排序
using namespace std;
void insertSort(int arr[], int len)
{
for (int i = 1; i < len; i++)
{
int j = i - 1;
int t = arr[i];
//从后往前,比当前值t大则往后移
while (j > -1 && t < arr[j])
{
arr[j + 1] = arr[j];
j--;
}
arr[j + 1] = t;
}
}
int main()
{
int array[] = { 34, 65, 12, 43, 67, 5, 78, 10, 3, 70 }, k;
int len = sizeof(array) / sizeof(int);
cout << "The orginal array are:" << endl;
for (k = 0; k < len; k++)
cout << array[k] << ",";
cout << endl;
insertSort(array, len);
cout << "The sorted array are:" << endl;
for (k = 0; k < len; k++)
cout << array[k] << ",";
cout << endl;
system("pause");
return 0;
}
快速排序
#include <iostream>
using namespace std;
void quickSort(int a[], int l, int r)
{
if (l < r)
{
int i = l, j = r, x = a[l];
while (i < j)
{
while (i < j&&a[j] >= x)
{
j--;
}
if (i < j)
{
a[i++] = a[j];
}
while (i < j&&a[i] <= x)
{
i++;
}
if (i < j)
{
a[j--] = a[i];
}
}
a[i] = x;
quickSort(a, l, i - 1);
quickSort(a, i + 1, r);
}
}
int main()
{
int array[] = { 34, 65, 12, 43, 67, 5, 78, 10, 3, 70 }, k;
int len = sizeof(array) / sizeof(int);
cout << "The orginal array are:" << endl;
for (k = 0; k < len; k++)
cout << array[k] << ",";
cout << endl;
quickSort(array, 0, len - 1);
cout << "The sorted array are:" << endl;
for (k = 0; k < len; k++)
cout << array[k] << ",";
cout << endl;
system("pause");
return 0;
}
归并排序
#include <iostream>
using namespace std;
void merge(int arr[], int tempArr[], int start, int mid, int end)
{
int i = start, j = mid + 1, k = 0;
while (i < mid + 1 && j < end + 1)
{
//谁小先放谁
if (arr[i] > arr[j])
tempArr[k++] = arr[j++];
else
tempArr[k++] = arr[i++];
}
//最后必有一边剩余,添加到后面即可
while (i < mid + 1)
{
tempArr[k++] = arr[i++];
}
while (j < end + 1)
{
tempArr[k++] = arr[j++];
}
//将排好的内容赋回原数组
for (i = 0, j = start; j < end + 1; i++, j++)
{
arr[j] = tempArr[i];
}
}
//主要就是递归的实现
void mergeSort(int arr[], int tempArr[], int start, int end)
{
if (start < end)
{
int mid = (start + end) / 2;
mergeSort(arr, tempArr, start, mid);
mergeSort(arr, tempArr, mid + 1, end);
merge(arr, tempArr, start, mid, end);
}
}
int main()
{
int array[] = { 34, 65, 12, 43, 67, 5, 78, 10, 3, 70 }, k;
int len = sizeof(array) / sizeof(int);
int tempArray[10] = { 0 };
cout << "The orginal array are:" << endl;
for (k = 0; k < len; k++)
cout << array[k] << ",";
cout << endl;
mergeSort(array, tempArray, 0, len - 1);
cout << "The sorted array are:" << endl;
for (k = 0; k < len; k++)
cout << array[k] << ",";
cout << endl;
system("pause");
return 0;
}
堆排序
#include <iostream>
using namespace std;
//数组arr局部调整为最大堆的实现,i为待调整元素下标,len为数组长度
void heapAdjust(int arr[], int i, int len)
{
int child, temp;
for (; 2 * i + 1 < len; i = child)
{
// 子结点的位置 = 2 * 父结点的位置 + 1
child = 2 * i + 1;
// 得到子结点中键值较大的结点,因为是调整为最大堆
if (child < len - 1 && arr[child] < arr[child + 1])
{
child++;
}
//如果较大的子结点大于父结点那么把较大的子结点往上移动,替换它的父结点
if (arr[i] < arr[child])
{
temp = arr[i];
arr[i] = arr[child];
arr[child] = temp;
}
else
break;
}
}
//堆排序的实现
void heapSort(int arr[], int len)
{
int i;
//数组arr调整为最大堆,调整完之后第一个元素是序列的最大的元素
for (i = len / 2 - 1; i >= 0; i--)
{
heapAdjust(arr, i, len);
}
//将第1个元素与当前最后一个元素交换,保证当前的最后一个位置的元素都是现在的这个序列中最大的
for (i = len - 1; i > 0; i--)
{
int temp = arr[0];
arr[0] = arr[i];
arr[i] = temp;
// 不断缩小调整heap的范围,每一次调整完毕保证第一个元素是当前序列的最大值
heapAdjust(arr, 0, i);
}
}
int main()
{
int array[] = { 34, 65, 12, 43, 67, 5, 78, 10, 3, 70 }, k;
int len = sizeof(array) / sizeof(int);
int temparray[10] = { 0 };
cout << "the orginal array are:" << endl;
for (k = 0; k < len; k++)
cout << array[k] << ",";
cout << endl;
heapSort(array, len);
cout << "the sorted array are:" << endl;
for (k = 0; k < len; k++)
cout << array[k] << ",";
cout << endl;
system("pause");
return 0;
}
堆排序的一个实例过程:
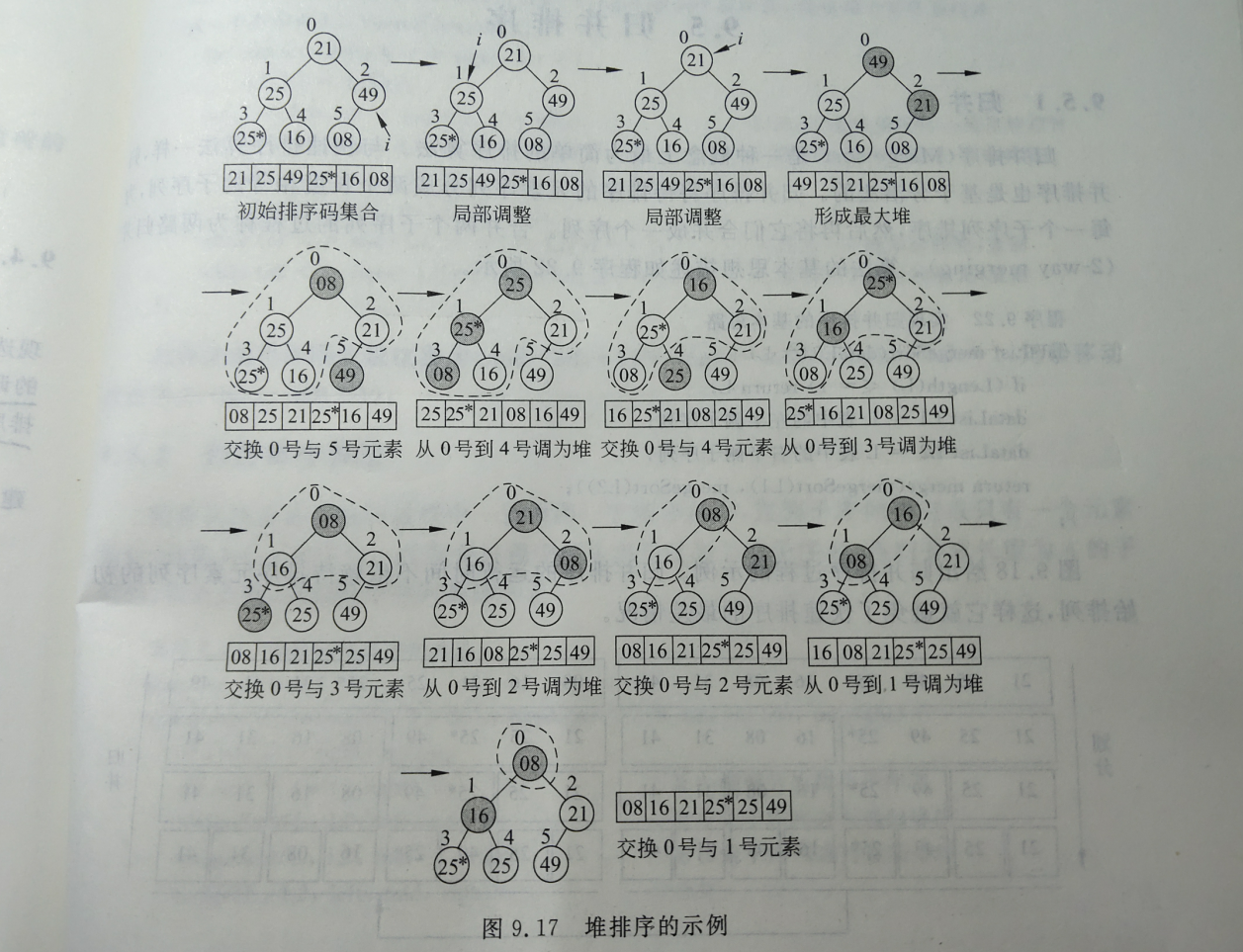
参考:
1.各种排序算法总结
2.十大经典排序算法(动图演示)
3.十种排序算法总结