堆:
需满足两个条件:
1、是一个完全二叉树
2、parent > child (大顶堆)
完全二叉树,确保可以用数组来表示,并且从任意节点开始出发,可以轻松得到其父节点和两个子节点。
对于节点i,parent = (i - 1) / 2, c1 = i * 2 + 1, c2 = i * 2 + 2
heapify:
可以把一个完全平方树看成很多个子树,每个子树就3个元素,对这个子树按照parent>child的规则进行调整,调整后,再递归的对其子节点进行判断。这个过程称为heapify。
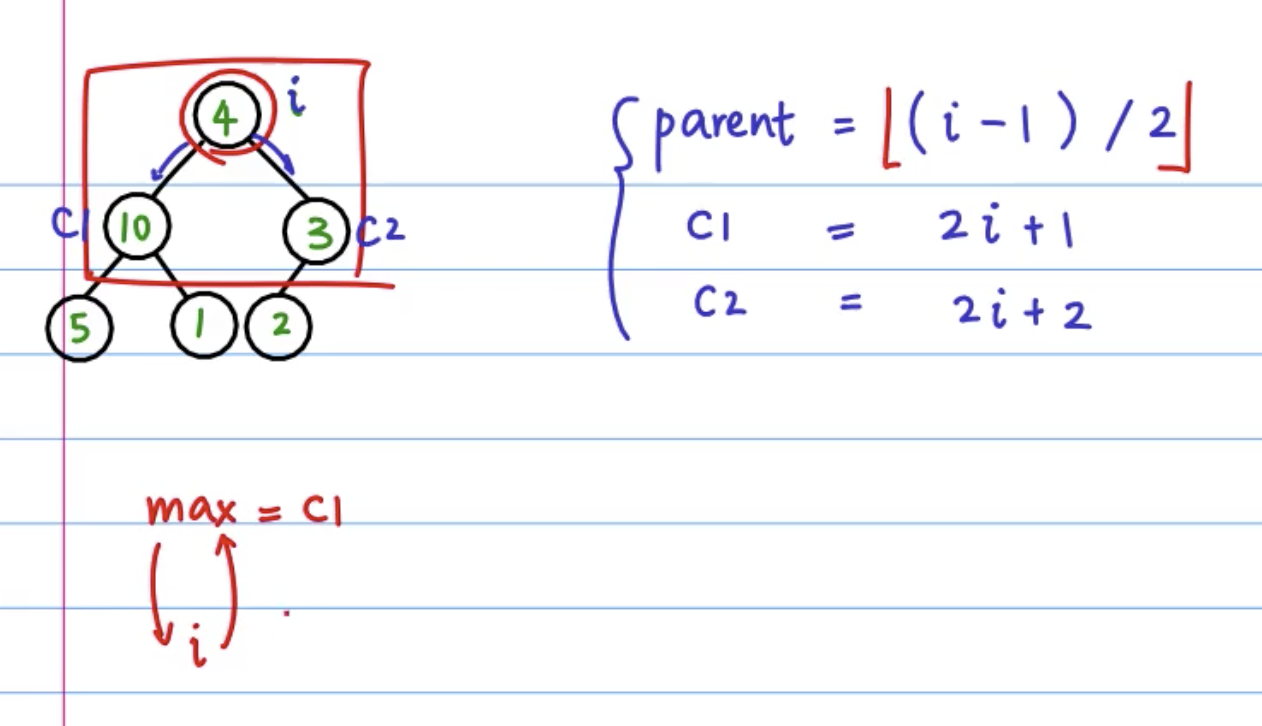
代码如下:
public void heapify(int[] tree, int n, int i) {
int max = i;
int c1 = i * 2 + 1;
int c2 = i * 2 + 2;
if (c1 < n && tree[c1] > tree[max])
max = c1;
if (c2 < n && tree[c2] > tree[max])
max = c2;
if (max != i) {
swap(tree, max, i);
heapify(tree, n, max);
}
}
构建堆:
将一个数组构造成一个堆,只需要从最后一个节点的父节点开始,往前遍历,对每个节点进行heapify。最后这个数组就是一个堆。
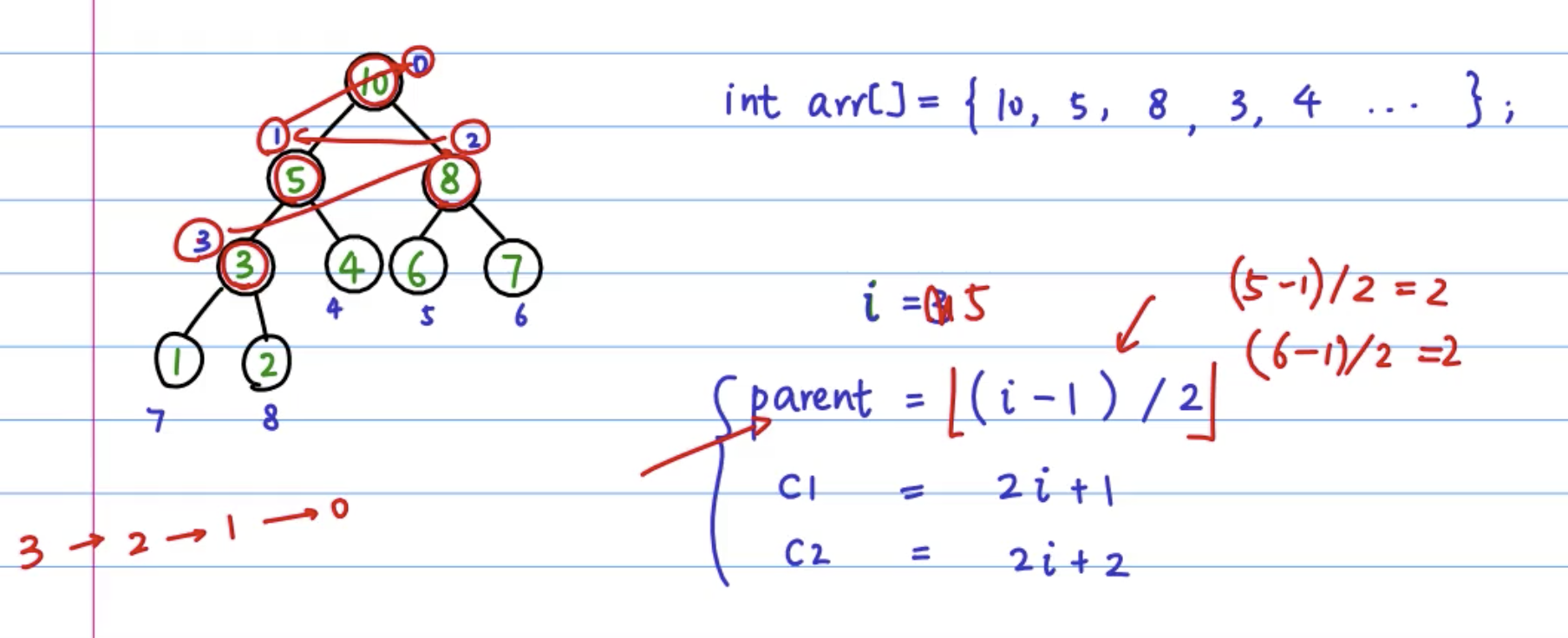
代码如下:
public void buildHeap(int[] tree, int n) {
int lastNode = n - 1;
int parent = (lastNode - 1) / 2;
for (int i = parent; i >= 0; --i) {
heapify(tree, n, i);
}
}
堆排序:
利用堆的性质,来进行排序。
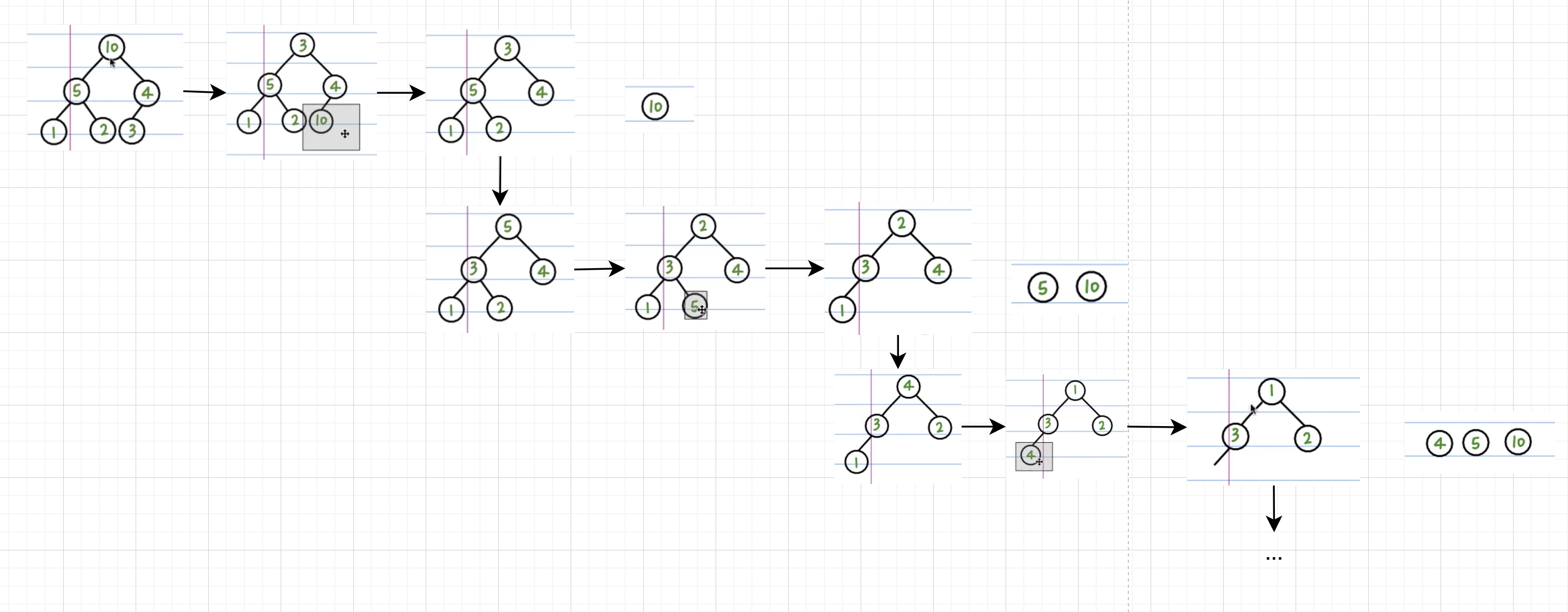
由上图可以看出整个过程就是将最大元素(第一个元素)与最后一个元素进行交换,然后将剩下的n-1个元素进行 heapify 操作,再将最大元素与倒数第二个元素进行交换。。。
代码如下:
public void heapSort(int[] tree) {
buildHeap(tree, tree.length);
for (int i = tree.length - 1; i >= 0; --i) {
swap(tree, 0, i);
heapify(tree, i, 0);
}
}
堆排序完整代码:
public class HeapSort{
public static void swap(int[] arr, int a, int b) {
int t = arr[a];
arr[a] = arr[b];
arr[b] = t;
}
public void heapify(int[] tree, int n, int i) {
int max = i;
int c1 = i * 2 + 1;
int c2 = i * 2 + 2;
if (c1 < n && tree[c1] > tree[max])
max = c1;
if (c2 < n && tree[c2] > tree[max])
max = c2;
if (max != i) {
swap(tree, max, i);
heapify(tree, n, max);
}
}
public void buildHeap(int[] tree, int n) {
int lastNode = n - 1;
int parent = (lastNode - 1) / 2;
for (int i = parent; i >= 0; --i) {
heapify(tree, n, i);
}
}
public void heapSort(int[] tree) {
buildHeap(tree, tree.length);
for (int i = tree.length - 1; i >= 0; --i) {
swap(tree, 0, i);
heapify(tree, i, 0);
}
}
public static void main(String[] args) {
int[] arr = {1, 4, 9, 3, 5, 2, 7, 0, 6, 8};
HeapSort sort = new HeapSort();
sort.heapSort(arr);
System.out.println(Arrays.toString(arr));
}
}
参考: