4.2深度卷积网络
觉得有用的话,欢迎一起讨论相互学习~
吴恩达老师课程原地址
参考文献
[残差网络]--He K, Zhang X, Ren S, et al. Deep Residual Learning for Image Recognition[J]. 2015:770-778.
2.3残差网络Residual Networks(ResNets)
- 非常非常深的网络是很难训练的,因为存在梯度消失和梯度爆炸的问题。使用跳远连接(skip connections)
- 它可以从某一网络层获取激活,然后迅速反馈给另外一层,甚至是神经网络的更深层,可以利用跳远连接构建能够训练深度网络的ResNets
Residual block
- Residual Networks残差网络由残差块构成,对于一个“普通的神经网络层的结构”而言,神经层(a^{[l]})到(a^{[l+1]})再到(a^{[l+2]})
网络的主路径"Main Path"可表示为:
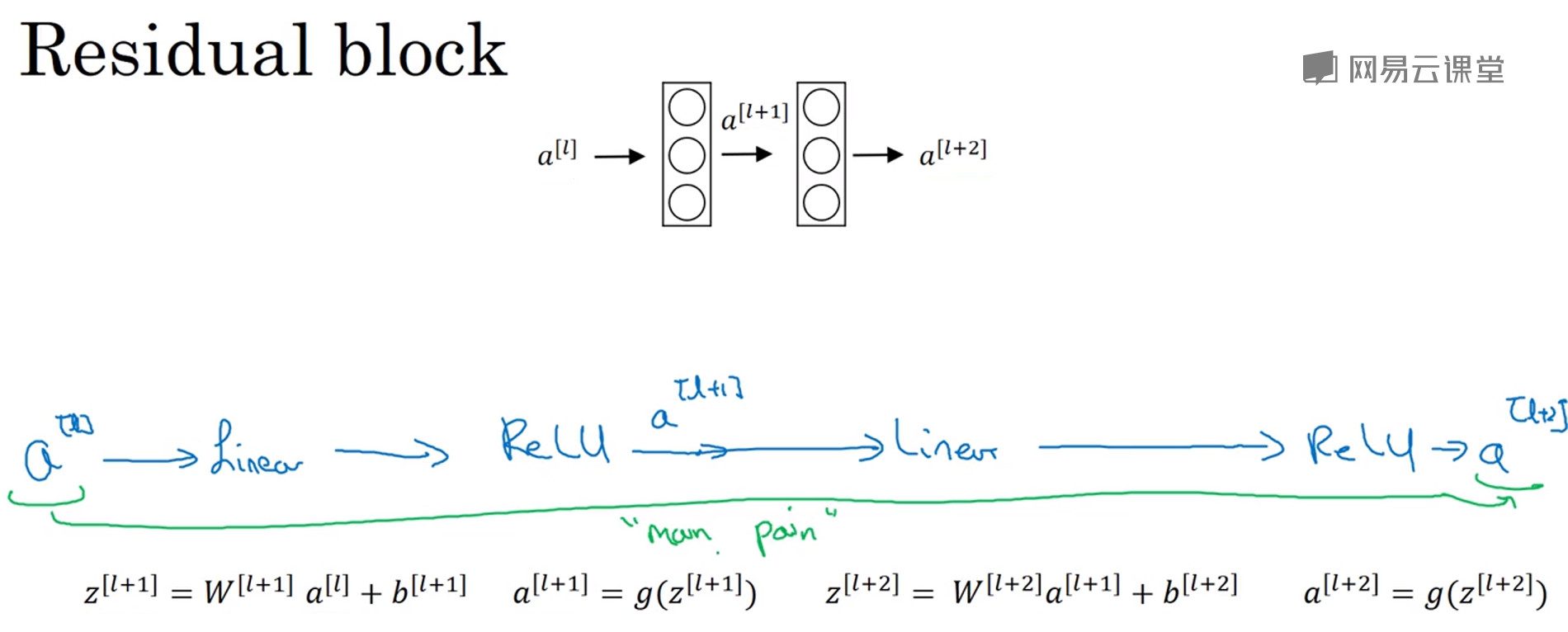
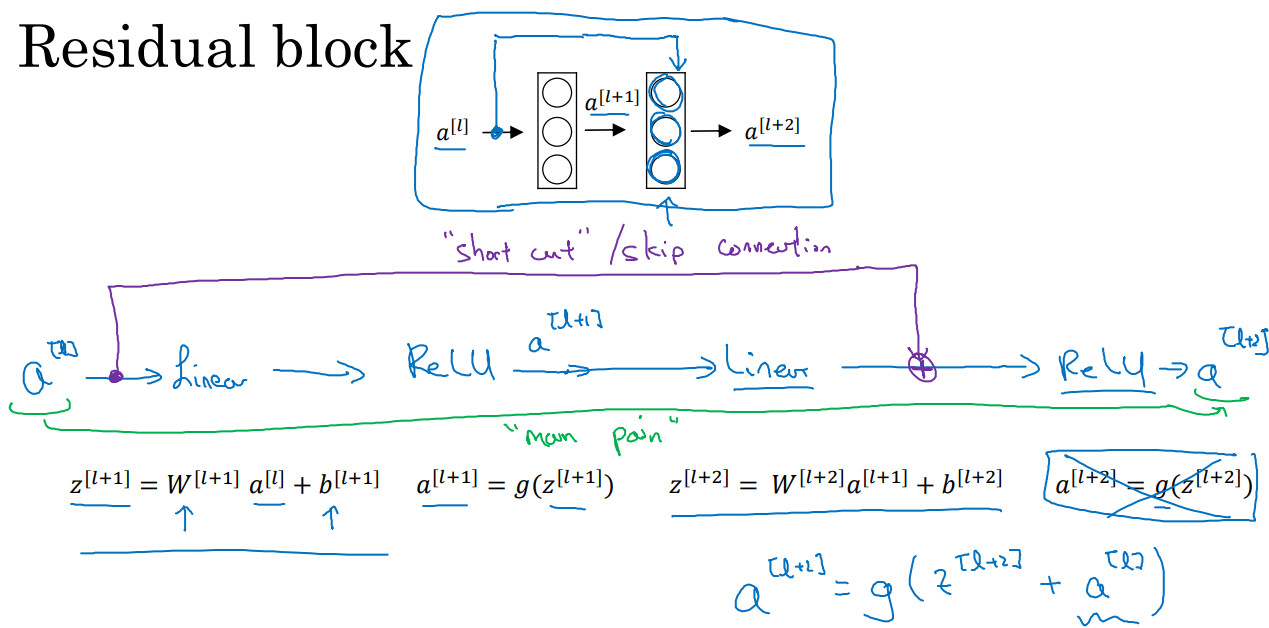
- 但是对于残差网络,(a^{[l]})可以拷贝到网络的深层,可以直接在ReLU非线性激活函数前加上(a^{[l]})。这被称为是"Short cut",不再沿着主路径传递。即原始公式中的(a^{[l+2]}=g(z^{[l+2]}))被替代为(a^{[l+2]}=g(z^{[l+2]}+a^{[l]})),也就是说加上的这个(a^{[l]})产生了一个残差块。
- "跳远连接(skip connection)"就是指(a^{[l]})跳过一层或者好几层,从而将信息传递给神经网络的更深层。
- ResNet的发明者认为使用残差块能够训练更深的神经网络,所以构建一个ResNet网络就是通过将很多这样的残差块堆积在一起,形成一个深度神经网络。
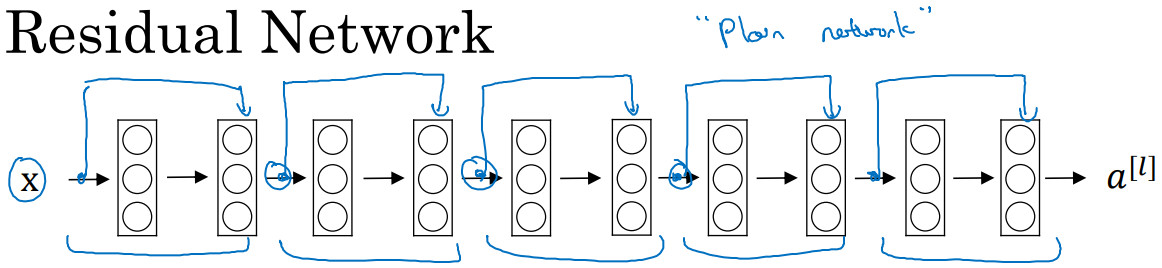
Residual Networks(ResNets)残差网络构造方法与优势
对于一个"Plain Network普通网络",把它变为ResNet的方法是加上所有的跳远连接(skip connections).每两层增加一个跳远连接构成一个残差块。如图所示,五个残差块连接在一起构成一个残差网络。
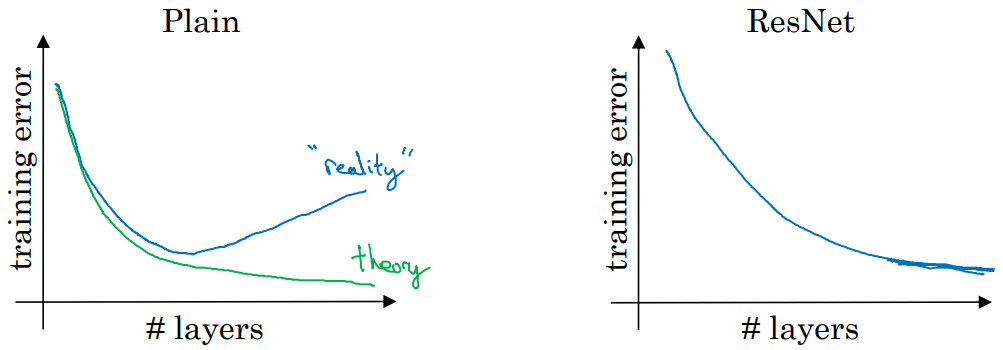
- 理论上说越深的神经网络应该会取得更好的结果,但是实际上对于普通网络随着神经网络网络层数的增加,训练的误差会先下降再上升。因为随着网络层数的增加,优化算法会更加难以训练网络。
- 但是ResNets不一样,即使网络再深,训练的表现却不错,错误会更少。就算网络的深度达到了1000层也会取得不错的结果。这证明ResNet在训练深度网络方面非常有效。
2.4残差网络Residual Networks(ResNets)为什么有用
残差网络在训练集上的效果
- 通常情况下,一个网络深度越深,它在训练集上训练集上训练网络的效率有所减弱。
- 假设网络结构如下图所示,其中BigNN表示一个很大很深的神经网络模型,并且使用ReLU函数作为激活函数,且所有ReLU函数的输入值都是非负值。
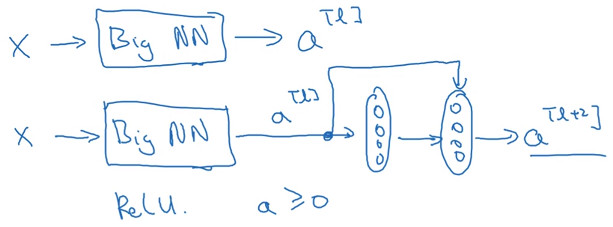
有如下计算式:
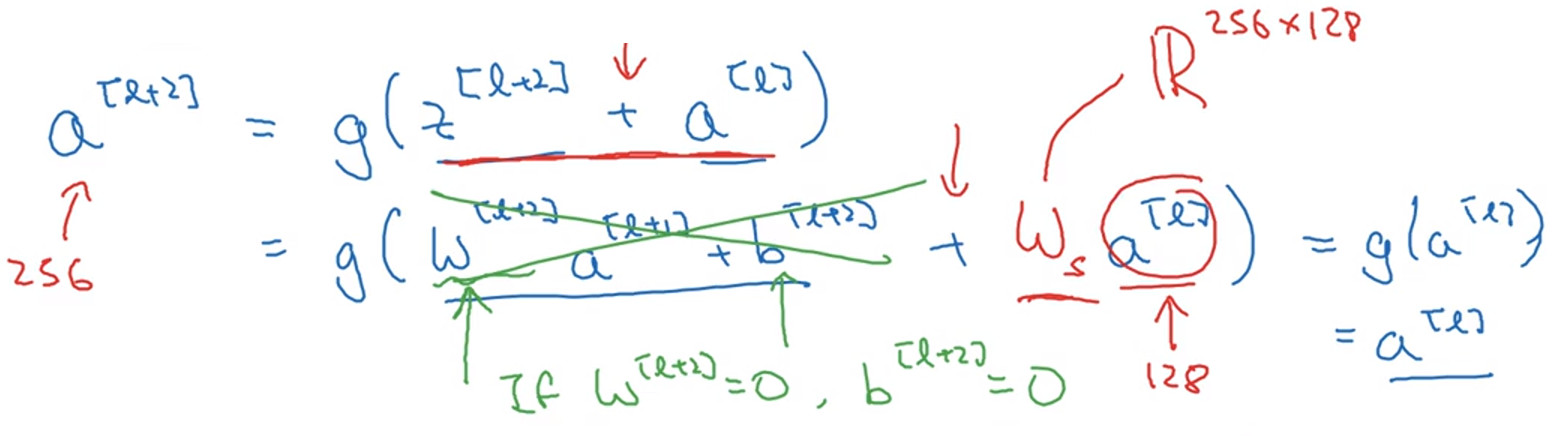
[a^{[l+2]}=g(z^{[l+2]}+a^{[l]})\
=g(w^{[l+2]}*a^{[l+1]}+b^{[l+2]}+a^{[l]})]
- 注意,如果我们使用了L2正则化,则会使公式中的w权值相应的减少。
- 这里设w和b均为零值,因为使用ReLU函数作为激活函数,并且激活函数的输入值是非负值则(a^{[l+2]}=g(a^{[l]})=a^{[l]})。
- NG认为残差网络起作用的主要原因是:这些残差块学习恒等函数非常容易,你能确定网络性能不会受到影响,很多时候甚至可以提高效率,至少效率不会降低。
残差块维度
- 对于残差块的跳跃连接的维度大小,因为残差块的设计中使用了相当多的“SAME”模式的卷积方式所以可以实现$$z^{[l+2]}+a^{[l]}的跳跃连接的操作$$即"SAME"卷积模式保持了维度。
- 但是如果(a^{[l+2]}和a^{[l]})的维度不一样,例如(a^{[l+2]})为256,(a^{[l]})的维度为128,则在(a^{[l]})前乘上一个可学习的变量(W_{s}),其中(W_{s})维度为(256*128)以保持维度的一致。
Plain网络(普通网络)加上ResNet单元
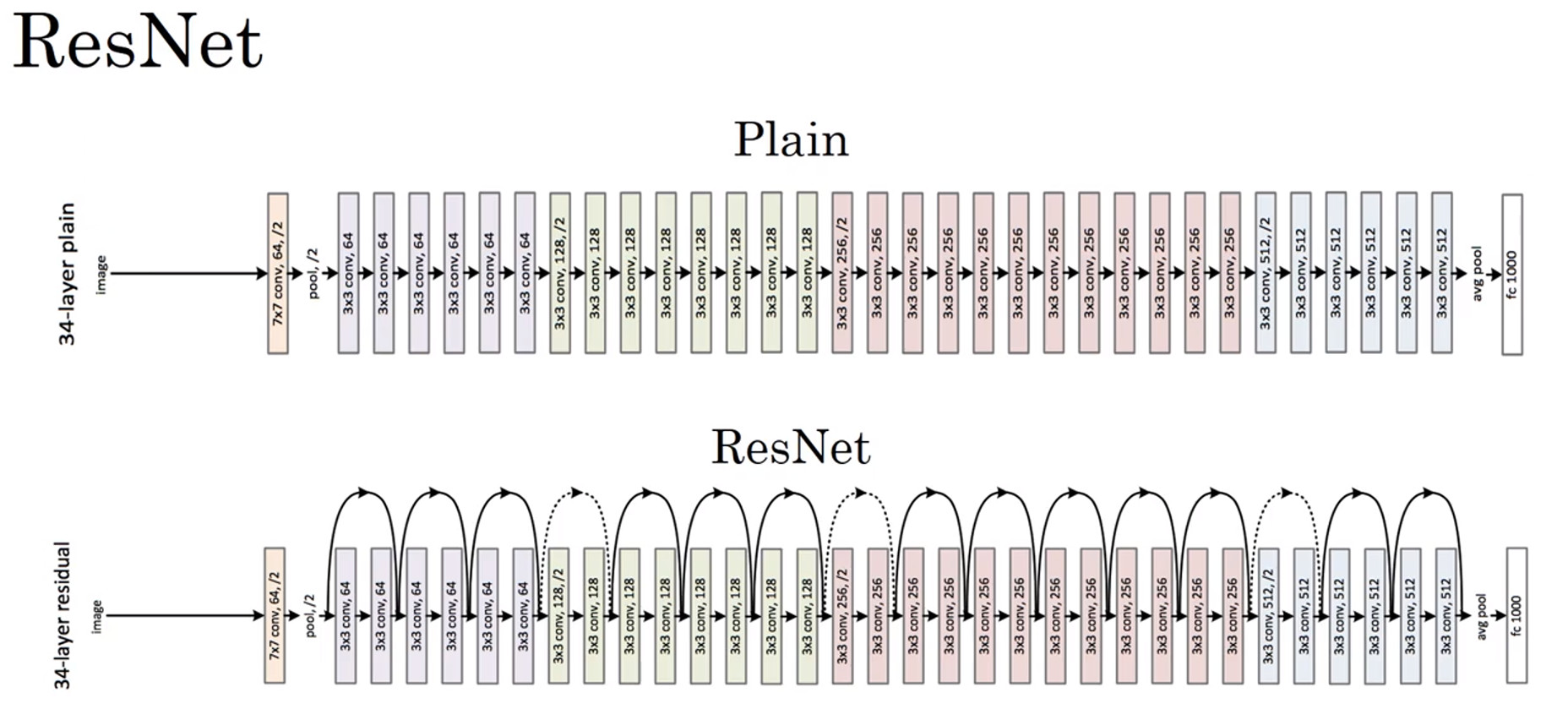
- 其中卷积层使用“SAME”卷积模式,保持特征图的维度信息即特征图的长和宽,但是对于残差块中有池化层的情况,则需要使用(W_s)调整维度,使跳跃连接的前后层可以保持一致的维度使其可以相加。



