[DeeplearningAI笔记]第二章1.9归一化normalization

[DeeplearningAI笔记]第二章1.9归一化normalization

觉得有用的话,欢迎一起讨论相互学习~

吴恩达老师课程原地址

1.9 归一化Normaliation

• 训练神经网络,其中一个加速训练的方法就是归一化输入(normalize inputs).
• 假设我们有一个训练集,它有两个输入特征,所以输入特征x是二维的,这是数据集的散点图.
  

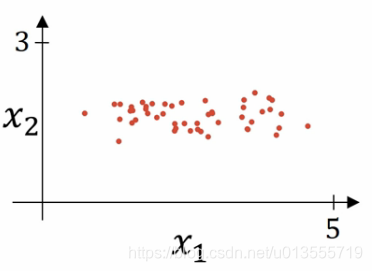
归一化输入需要两个步骤

第一步-零均值化

• subtract out or to zero out the mean 计算出u即x(i)的均值

[u=frac{1}{m}sum^{m}_{i=1}x^{(i)} ]

• u是一个向量,(x=x-u)每个训练数据(x)都是(x-u)的新值
• 意思是移动训练集,直到它完成零均值化

第二步-归一化方差

• 如上图所示:特征x1的方差比特征x2的方差要大得多,我们要做的是给(sigma)赋值.(sigma)是一个方差,它的每个特征都是方差.其中(sigma^2=frac{1}{m}sum^{m}_{i=1}x^{(i)}).元素(x^{(i)})表示每个特征的方差.我们已经对数据完成了零均值化,现在只需要将所有数据都除以向量(sigma^{2})

• 经过方差的归一化,数据分布变为:

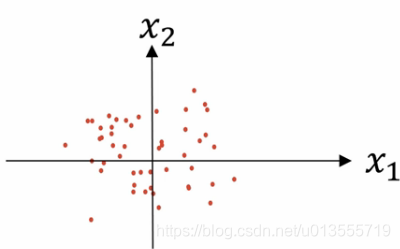
• 特征x1和特征x2的方差都等于1

• 注意:如果你要用它来调整数据,那么要用相同的(u和sigma^2)来归一化测试集和训练集.这个数据集都是通过相同的(u和sigma定义的相同的数据转换)其中(u和sigma都是通过训练数据集得来的)

为什么要归一化输入特征

• 如果不使用归一化,则这是个非常细长狭窄的代价函数,你要找的代价函数的最小值点应该在这里.(如图中箭头标示)
  

• 但是特征值在不同的取值范围内,例如x1取值范围从1到1000,特征x2的取值范围从0到1,结果是参数w1和w2值的范围或者比率完全不同,这些数据轴应该是w1和w2,为了直观理解,我标记为w和b,该函数的轮廓十分狭窄.

• 如果使用了归一化方法,代价函数更加对称

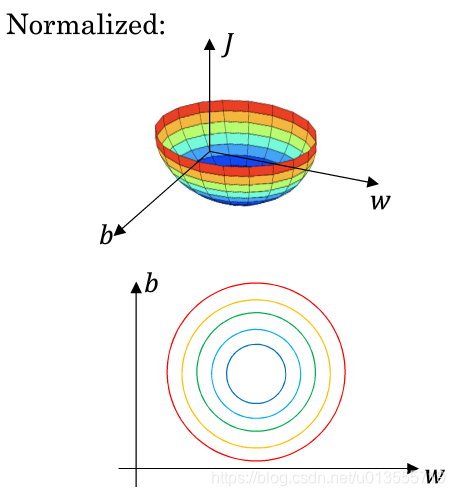
• 如果在不使用归一化方法且特征分布十分不均匀的数据集上的代价函数上运行梯度下降法,必须使用一个非常小的学习比率,因为如果是在这个位置,梯度下降法可能需要更多次迭代过程.

直到最后找到最小值.

• 但是如果函数是经过归一化的特征分布,那么会是一个更圆的轮廓,那么无论从哪个位置开始,梯度下降法都能够更直接地找到最小值,并且可以使用较大步长,而不是需要以较小步长反复执行.

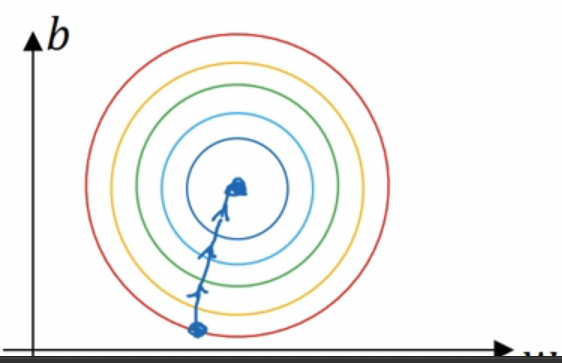
• 这只是一个二维特征的例子,实际上w是一个高维向量,因此用二维绘制w并不能正确的传达直观理解,但总的直观理解是代价函数会更圆一些,,前提是特征都在相似范围内,而不是从1到1000,0到1的差别很大的范围内,而是都在-1到1的范围内,或者相似偏差,这使得优化代价函数变的更简单更快捷.

• 实际上,如果特征x1范围在0~1之间,x2在-1~1之间,x3在1~2之间,它们是相似范围,所以会表现的很好,如果在不同的取值范围内,如其中一个从1到1000,另一个从0到1,这对优化算法十分不利,但是仅将它们设置为均化零值,假设方差为1,确保特征都在相似范围内,通常可以使算法运算得更快.

• 如果数据的不同特征值取值范围差异很大,那么归一化就很重要了,如果特征值处于相似范围,那么归一化就变得不那么重要了.