说来惭愧,一直自称为算法竞赛选手却从来没有认真了解过红黑树,这个C++的STL和Java多个容器都选择的数据结构必然有其过人之处。直到今天我才来学红黑树这个数据结构。
阅读本文至少需要先掌握查找二叉树的相关知识,如果有学习过诸如Treap树,Splay等其他平衡二叉树那么学习红黑树将会更加简单。不管怎样,根据博主的学习红黑树的经验来看,红黑树并不难以理解,恰恰相反它的每一种情况下的每一步操作都是有理有据的,只要思考明白这样做的原因你能很自然地理解红黑树。最然这样说,但是红黑树也并非能短时间内掌握,红黑树学习难点在于其变化之多,情况之复杂。所以静下心来看明白每一种变化情况的对策是学习红黑树的最好方法。
另外,因为博主也是从文末参考资料中各个前辈的博文中学习而来,所以尽管本文全本都是原创手打,依然难以避免在本文看到各个前辈的影子。本文首先是在记录博主的学习过程,也旨在以自己的理解试图找到一种更加简单的学习红黑树的办法。碍于博主水平有限,文章难免有错误与疏漏。如果读者看不懂不用怀疑肯定是博主的问题。那么废话不多说,我们就开始了。
(更新中,插入结点完成,删除结点未完成)
前置知识
首先红黑树是一棵二叉查找树,即树的每个结点都是一个插入的数据值,每个结点P的左子树的结点值都比P小,P的右子树的结点值都比P大。那么二叉查找树插入和查找值都是从根开始与当前结点比较,比当前结点小往左走,比当前大往右走,直到走到相等值或者空结点。这里要注意一点,插入终点一定是某个key相等结点,或者是空结点!
并且红黑树是一棵平衡树,亦即哪怕在恶劣情况下树也不会退化成一条链而是会平衡的。严格来说红黑树是弱平衡树,因为它只能保证不会存在一条根到叶节点的路径超过另一条路径的两倍(下面的红黑树性质4与性质5保证顶多就存在一条黑红交替的路径是另一条黑色路径的两倍)。因此红黑树的树根为log2n级别的,这也是红黑树一次插入/查询的时间复杂度。
性质
同此同时,红黑树有着一些它自己独特的5个性质:
性质1,每个节点要么是黑色或者是红色的。
性质2,红黑树的根节点一定是黑色的。
性质3,每个叶子节点(NIL)是黑色的。(注意这里的叶节点NIL指的是无信息的结点)
性质4,每个红色结点的两个儿子结点一定都是黑色的。
性质5,任意一结点到每个叶子结点的路径都包含数量相同的黑结点。
读到这里的话,先不深究感性理解以下这几个性质。读到后面记得不断回看这几个性质,红黑树的所有操作都没有违背这几个性质,都在想办法用巧妙的变色/旋转等手段在规则下操作。
三个基本操作
然后红黑树不仅是二叉查找树,进一步的它是一棵平衡树,有着平衡树的两个基本维持平衡的操作:左旋,右旋。特别需要注意的是在左右旋转的过程中一定还要保持查找二叉树的性质左小右大,以左旋为例:左旋之后原本S结点的左子树就失去了,那么为了维持就把E的右子树移接为S的左子树,而且这样的移接是恰好符合性质的,因为S的左儿子的右子树必然是S左子树的最大子树。这里贴两幅动图帮助理解。
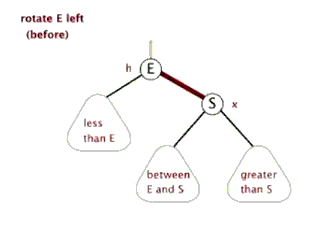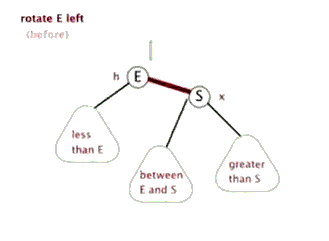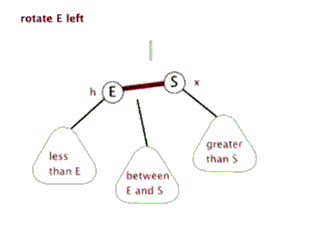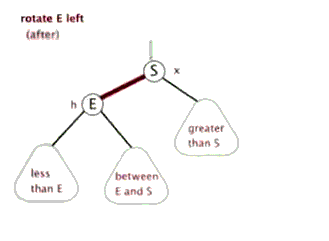

除了左旋右旋,红黑树还有一种操作就是:变色(红结点变黑/黑变红)。那么这三个操作成为了红黑树维持平衡的三个基本操作。
插入结点
那么讨论完三个基本操作之后我们就开始真正开始改变红黑树的结构了,首先是插入结点。如上文所述,红黑树首先是一棵二叉查找树,所有它的插入也是跟当前结点值比较然后往左往右走,直到找到相等值或者走到空结点。
那么我们这个过程我们首先要考虑的问题就是:插入结点应当是红色的还是黑色的?我们不妨分析一下,如果插入点是黑色,那么本来红黑树是平衡的满足性质5,但是插入后该点子树的黑色结点必定多了一个黑色结点破坏性质5导致我们必须得做自平衡操作。如果插入点是红色,那么它一定不会破坏性质5,但是在插入位置父亲结点是红色时候才会破坏性质4。那么显然插入红色结点麻烦事少一点。那么我们以下的插入操作都是插入红色结点。
首先是三种简单的情况,它们的应对方法是显然的(所以这里就直接一笔带过,减轻读者继续来分情况的负担):
① 在空树插入结点:直接插入并且为了满足性质2变化为黑点。
②插入点值存在:这种情况就不需要对树的结构发生任何改变(颜色也不能改)了,直接把结点副本数+1即可.
③插入点父亲为黑色结点:我们发现直接在黑色结点下插入这个红色结点不会违背性质,那么直接插入即可。
那么除了上面三种情况就剩下:插入点父亲为红色结点 这一种情况。我们先得分析违背了什么性质:显然出现了连续的两辈的红色结点,违背了性质4。所以一下我们主要的工作就是想办法满足性质4。
但是这一种情况是插入中最复杂的,也是红黑树插入部分的重点(经过上面的一笔带过,其实你就只需重点记住这三种情况),我们得继续细分:
一,父亲兄弟结点存在且为红色结点
对于这种情况,我们想因为插入点父亲结点和父亲兄弟都是红色的,父亲兄弟的父亲(即爷爷结点)和父亲的儿子结点必定是黑色的(根据性质4)。那么我们就想能不能把爷爷这一辈和父亲这一辈 这两辈的颜色换一换,说干就干我们就把爷爷辈和父亲辈的颜色对换。一切看起来都还不错,但是注意此时爷爷结点变成了红色!那么此时有可能爷爷结点违背了性质4!!不用慌,此时我们就把爷爷结点当成是新的插入结点继续向上调整即可。

呼呼看了上面的这种情况,接下来肯定是父亲兄弟不存在或者是存在但是是黑色的。对,但是我们得将这种情况分为父亲是爷爷的左儿子/右儿子,值得庆幸的是这两种情况是对称的那么只要读者理解的第一种情况,那么就能轻易理解第二种情况。
二,父亲兄弟节点不存在或者存在为黑色结点,且父亲兄弟为爷爷的左儿子
于是我们细讲对称情况的第一种,左儿子。比起 一(上文) 这种情况,现在我们的父亲兄弟是黑色的了(或者父亲根本就没有兄弟),带来的影响是什么?影响是父亲和同辈不同色,就不能用上次的两辈交换颜色的做法了。那么我们想另一个办法:此时插入点和父亲都是红色,要是能只把父亲移到右边就好了。哎!!移动只要一种方式,那就是旋转。但是此时我们的爷爷结点是黑色的,如果我们贸然右旋必然会破环黑色平衡(性质5).于是我们先把父亲和爷爷的颜色交换,然后右旋。这样会违背性质吗?不会,舒服了。
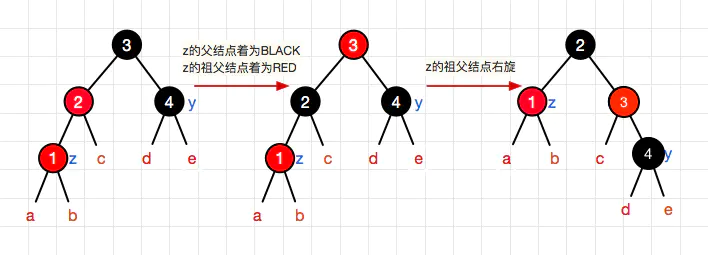
三,父亲兄弟节点不存在或者存在为黑色结点,且父亲兄弟为爷爷的右儿子
发现了没,与二是相反的,那么我们自然不必煞费苦心再次想个新策略。直接通过把父亲左旋就能转变为情况二。
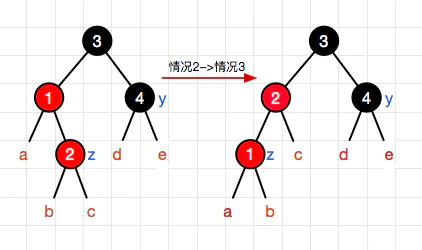
删除结点
讨论完插入情况之后就是平衡树得另一种操作:删除结点。删除结点是比插入更加复杂得操作,但是跟着步骤分析也不难。
参考资料: