Rotation Lock Puzzle
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1668 Accepted Submission(s): 530
Problem Description
Alice was felling into a cave. She found a strange door with a number square matrix. These numbers can be rotated around the center clockwise or counterclockwise. A fairy came and told her how to solve this puzzle lock: “When the sum of main diagonal and anti-diagonal is maximum, the door is open.”.
Here, main diagonal is the diagonal runs from the top left corner to the bottom right corner, and anti-diagonal runs from the top right to the bottom left corner. The size of square matrix is always odd.
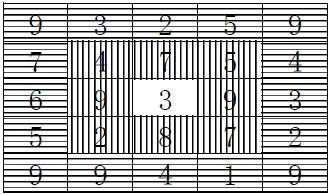
This sample is a square matrix with 5*5. The numbers with vertical shadow can be rotated around center ‘3’, the numbers with horizontal shadow is another queue. Alice found that if she rotated vertical shadow number with one step, the sum of two diagonals is maximum value of 72 (the center number is counted only once).
Here, main diagonal is the diagonal runs from the top left corner to the bottom right corner, and anti-diagonal runs from the top right to the bottom left corner. The size of square matrix is always odd.

This sample is a square matrix with 5*5. The numbers with vertical shadow can be rotated around center ‘3’, the numbers with horizontal shadow is another queue. Alice found that if she rotated vertical shadow number with one step, the sum of two diagonals is maximum value of 72 (the center number is counted only once).
Input
Multi cases is included in the input file. The first line of each case is the size of matrix n, n is a odd number and 3<=n<=9.There are n lines followed, each line contain n integers. It is end of input when n is 0 .
Output
For each test case, output the maximum sum of two diagonals and minimum steps to reach this target in one line.
Sample Input
5
9 3 2 5 9
7 4 7 5 4
6 9 3 9 3
5 2 8 7 2
9 9 4 1 9
0
Sample Output
72 1
Source
题意:一个边长为奇数N(3<=N<=9)的正方形矩阵,其中的小正方形矩阵可以围绕中心做顺时针或者逆时针旋转,求旋转的后的正对角线和副对角线的最大的总和,和最小旋转的次数。
分析:依次枚举每一层,在每一层中,求能够到达对角线的四个点的和最大是多少,然后记录下得到每层最大值的旋转的次数是多少。

#pragma comprint(linker, "/STACK:1024000000,1024000000") #include<cstdio> #include<string> #include<iostream> #include<cstring> #include<cmath> #include<stack> #include<queue> #include<vector> #include<map> #include<stdlib.h> #include<time.h> #include<algorithm> #define LL __int64 #define FIN freopen("in.txt","r",stdin) using namespace std; const int INF=0x3f3f3f3f; int main() { int n,ans,anst,t,t1,sum,s; int val[15][15]; while(scanf("%d",&n)&&n) { anst=ans=0; memset(val,0,sizeof(val)); for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) scanf("%d",&val[i][j]); for(int i=1;i<=n/2;i++) { sum=-INF; for(int j=0;j<n-(i-1)*2-1;j++) { s=val[i][i+j]+val[i+j][n-i+1]+val[n-i+1][n-i+1-j]+val[n-i+1-j][i]; if(sum<s) { sum=s; t1=j<(n-i-j)?j:(n-i-j); } else if(sum==s) { t=j<(n-i-j)?j:(n-i-j); if(t<t1) t1=t; } } ans+=sum; anst+=t1; } ans+=val[n/2+1][n/2+1]; printf("%d %d ",ans,anst); } return 0; }
