Solve this interesting problem
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1728 Accepted Submission(s): 517
Problem Description
Have you learned something about segment tree? If not, don’t worry, I will explain it for you.
Segment Tree is a kind of binary tree, it can be defined as this:
- For each node u in Segment Tree, u has two values: Lu and Ru.
- If Lu=Ru, u is a leaf node.
- If Lu≠Ru, u has two children x and y,with Lx=Lu,Rx=⌊Lu+Ru2⌋,Ly=⌊Lu+Ru2⌋+1,Ry=Ru.
Here is an example of segment tree to do range query of sum.
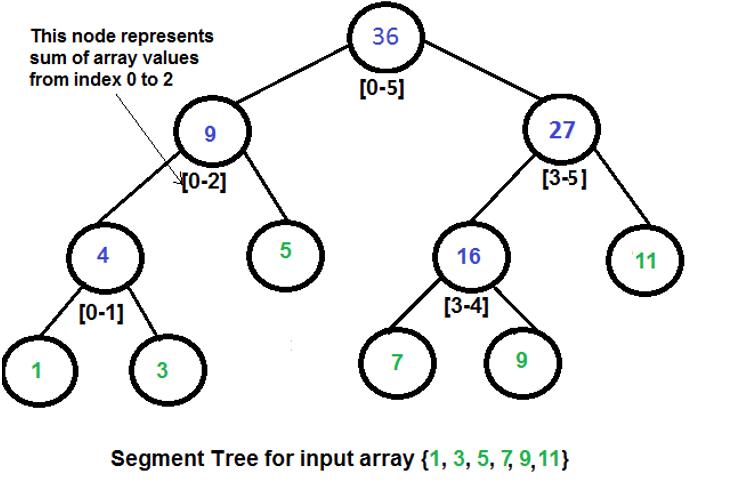
Given two integers L and R, Your task is to find the minimum non-negative n satisfy that: A Segment Tree with root node's value Lroot=0 and Rroot=n contains a node u with Lu=L and Ru=R.
Segment Tree is a kind of binary tree, it can be defined as this:
- For each node u in Segment Tree, u has two values: Lu and Ru.
- If Lu=Ru, u is a leaf node.
- If Lu≠Ru, u has two children x and y,with Lx=Lu,Rx=⌊Lu+Ru2⌋,Ly=⌊Lu+Ru2⌋+1,Ry=Ru.
Here is an example of segment tree to do range query of sum.

Given two integers L and R, Your task is to find the minimum non-negative n satisfy that: A Segment Tree with root node's value Lroot=0 and Rroot=n contains a node u with Lu=L and Ru=R.
Input
The input consists of several test cases.
Each test case contains two integers L and R, as described above.
0≤L≤R≤109
LR−L+1≤2015
Each test case contains two integers L and R, as described above.
0≤L≤R≤109
LR−L+1≤2015
Output
For each test, output one line contains one integer. If there is no such n, just output -1.
Sample Input
6 7
10 13
10 11
Sample Output
7
-1
12
Source
题意:给定区间[L,R],能否生成包含该区间的线段树,如果能,包含该段的线段树[0,n]的n的最小值是多少
分析:区间[L,R]可能是父区间的左孩子也可能是父区间的右孩子,所以有可能有四种情况,[L,R+(R-L+1)],[L,R+(R-L+1)-1],[L-(R-L+1),R],[L-(R-L+1)-1,R]

#pragma comment(linker, "/STACK:1024000000,1024000000") #include<cstdio> #include<string> #include<iostream> #include<cstring> #include<cmath> #include<stack> #include<queue> #include<vector> #include<map> #include<stdlib.h> #include<algorithm> #define LL __int64 using namespace std; const int INF=0x3f3f3f3f; LL L,R,ans; void DFS(LL l,LL r) { LL len=r-l+1; //区间长度 if(r>=ans) return ; if(l==0) { ans=r; return ; } //结束递归 if(len>l) return ; DFS(2*l-r-1,r); DFS(2*l-r-2,r); DFS(l,2*r-l); DFS(l,2*r-l+1); } int main() { //freopen("in.txt","r",stdin); while(scanf("%I64d %I64d",&L,&R)!=EOF) { ans=INF; DFS(L,R); if(ans==INF) cout<<"-1"<<endl; else cout<<ans<<endl; } return 0; }
