
%% 数据准备 % 清空环境变量 clear all; clc; citys = xlsread('c:UsersclementeDesktop erminal.xlsx','B2:C73'); ab1= [29 29 45.5 92 92 29]; % 五边形各点横坐标 最后回到第一个点 形成闭环 cd1= [125 58 57 85 125 125]; % 五边形各点纵坐标 最后回到第一个点 形成闭环 ab2= [45.5 92 92 45.5]; % 三角形各点横坐标 最后回到第一个点 形成闭环 cd2= [57 85 29 57]; % 三角形各点纵坐标 最后回到第一个点 形成闭环 ab3= [29 45.5 92 92 29 29]; % 五边形各点横坐标 最后回到第一个点 形成闭环 cd3= [58 57 29 12.5 13 58]; % 五边形各点纵坐标 最后回到第一个点 形成闭环 x=citys(:,1); y=citys(:,2); in1=inpolygon(x,y,ab1,cd1); in2=inpolygon(x,y,ab2,cd2); in3=inpolygon(x,y,ab3,cd3); figure(1); subplot(1,3,1); plot(ab1,cd1,x(in1),y(in1),'ro',x(~in1),y(~in1),'b<') subplot(1,3,2); plot(ab2,cd2,x(in2),y(in2),'ro',x(~in2),y(~in2),'b<') subplot(1,3,3); plot(ab3,cd3,x(in3),y(in3),'ro',x(~in3),y(~in3),'b<') city1=citys(in1,:); city2=citys(in2,:); city3=citys(in3,:); basepoint=[110 0]; %无人机出发 基地的坐标 city1=[basepoint;city1;basepoint]; %基地加入到第一个聚类区域 city2=[basepoint;city2;basepoint]; %基地加入到第二个聚类区域 city3=[basepoint;city3;basepoint]; %基地加入到第三个聚类区域 %% 第一个聚类群 % 程序运行计时开始 t0 = clock; %% 计算城市间距离 n = size(city1,1) -1; %城市数 起点,终点同一个要减1 D = zeros(n,n); for i = 1:n for j = 1:n if i ~= j D(i,j) = sqrt(sum( ( city1(i,:) - city1(j,:) ).^2 ) ); %两点之间的距离 else D(i,j) = 1e-4; %为保证启发函数的分母不为0,设定的对角矩阵修正值为一个较小正值 end end end %% 初始化参数 m = 27+1; % 蚂蚁数量最好接近城市数量的1.5倍 +1是因为新加入了基地 alpha = 1; % 信息素重要程度因子[1,4]最好 beta = 5; % 启发函数重要程度因子 5最好 vol = 0.2; % 信息素挥发(volatilization)因子 Q = 10; % 常系数 Heu_F = 1./D; % 启发函数(heuristic function) Tau = ones(n,n); % 信息素矩阵 Table = zeros(n,n); % 路径记录表 iter = 1; % 迭代次数初值 iter_max = 300; % 最大迭代次数 [100,500] Route_best = zeros(iter_max,n); % 各代最佳路径 Length_best = zeros(iter_max,1); % 各代最佳路径的长度 Length_ave = zeros(iter_max,1); % 各代路径的平均长度 Limit_iter = 0; % 程序收敛时迭代次数 %% 迭代寻找最佳路径 while iter <= iter_max % 随机产生各个蚂蚁的起点城市 start = zeros(m,1); for i = 1:m temp = randperm(n); %randperm函数打乱顺序 1-n随机排序 start = temp(1); end Table(:,1) = start; %路径记录表 % 构建解空间 citys_index = 1:n; % 逐个蚂蚁路径选择 for i =1:m % 逐个城市路径选择 for j = 2:n tabu = Table(i,1:(j - 1)); % 已访问的城市集合(禁忌表) allow_index = ~ismember(citys_index,tabu); % 1.ismember函数判断一个变量中的元素是否在另一个变量中出现,返回0-1矩阵; allow = citys_index(allow_index); % 待访问的城市集合 P = allow; % 计算城市间转移概率 for k = 1:length(allow) P(k) = Tau(tabu(end),allow(k))^alpha * Heu_F(tabu(end),allow(k))^beta; %线路选择概率的分子 end P = P / sum(P); %线路选择概率的分母 % 轮盘赌法选择下一个访问城市 Pc = cumsum(P); %cumsum函数用于求变量中累加元素的和,如A=[1,2,3,4,5],那么cumsum(A)=[1,3,6,10,15] target_index = find(Pc >= rand); target = allow(target_index(1)); Table(i,j) = target; end end % 计算各个蚂蚁的路径距离 Length = zeros(m,1); for i = 1:m Route = Table(i,:); for j = 1:(n - 1) Length(i) = Length(i) + D(Route(j),Route(j + 1)); end Length(i) = Length(i) + D(Route(n),Route(1)); %最后回到起点 end % 计算最短路径距离及平均距离 if iter == 1 [min_Length, min_index] = min(Length); Length_best(iter) = min_Length; Length_ave(iter) = mean(Length); Route_best(iter,:) = Table(min_index,:); Limit_iter = 1; else [min_Length,min_index] = min(Length); Length_best(iter) = min(Length_best(iter - 1),min_Length); Length_ave(iter) = mean(Length); if Length_best(iter) == min_Length Route_best(iter,:) = Table(min_index,:); Limit_iter = iter; else Route_best(iter,:) = Route_best((iter - 1),:); end end % 更新信息素 Delta_Tau = zeros(n,n); %信息素增量 % 逐个蚂蚁计算 for i = 1:m % 逐个城市计算 for j = 1:(n - 1) Delta_Tau(Table(i,j),Table(i,j+1)) = Delta_Tau(Table(i,j),Table(i,j+1)) + Q/Length(i); %Q为常数 end Delta_Tau(Table(i,n),Table(i,1)) = Delta_Tau(Table(i,n),Table(i,1)) + Q/Length(i); %最后回到第一个城市的最终值 end Tau = (1 - vol) * Tau + Delta_Tau; %信息素挥发损失的剩下部分+新的增量 % 迭代次数加1,清空路径记录表 iter = iter + 1; Table = zeros(m,n); end %% 结果显示 [Shortest_Length,index] = min(Length_best); Shortest_Route = Route_best(index,:); Time_Cost = etime(clock,t0); disp(['最短距离:' num2str(Shortest_Length)]); disp(['最短路径:' num2str( [Shortest_Route Shortest_Route(1)] )]); disp(['收敛迭代次数:' num2str(Limit_iter)]); disp(['程序执行时间:' num2str(Time_Cost),'秒']); %% 绘图 figure(2) plot([ city1(Shortest_Route,1);city1(Shortest_Route(1),1) ], [ city1(Shortest_Route,2);city1(Shortest_Route(1),2) ], 'k.-','Markersize',20); set(gca,'LineWidth',1.5); %边框加粗,美观 grid on; for i = 1:size(city1,1) text(city1(i,1),city1(i,2),[' ' num2str(i)]); end text(city1(1,1),city1(1,2),' 起飞基地'); xlabel('城市位置横坐标'); ylabel('城市位置纵坐标'); title(['ACA最优化路径(最短距离:' num2str(Shortest_Length) ')']); figure(3); %收敛图 subplot(1,3,1); plot(1:iter_max,Length_best,'b'); set(gca,'LineWidth',1.5); %边框加粗,美观 legend('最短距离'); xlabel('迭代次数'); ylabel('距离'); title('算法收敛轨迹'); set(gca,'LineWidth',1.5); %边框加粗,美观 %% 第二个聚类群 % 程序运行计时开始 t0 = clock; %% 计算城市间距离 n = size(city2,1)-1; %城市数 起点,终点同一个要减1 D = zeros(n,n); for i = 1:n for j = 1:n if i ~= j D(i,j) = sqrt(sum( ( city2(i,:) - city2(j,:) ).^2 ) ); %两点之间的距离 else D(i,j) = 1e-4; %为保证启发函数的分母不为0,设定的对角矩阵修正值为一个较小正值 end end end %% 初始化参数 m = 17+1; % 蚂蚁数量最好接近城市数量的1.5倍 alpha = 1; % 信息素重要程度因子[1,4]最好 beta = 5; % 启发函数重要程度因子 5最好 vol = 0.2; % 信息素挥发(volatilization)因子 Q = 10; % 常系数 Heu_F = 1./D; % 启发函数(heuristic function) Tau = ones(n,n); % 信息素矩阵 Table = zeros(n,n); % 路径记录表 iter = 1; % 迭代次数初值 iter_max = 300; % 最大迭代次数 [100,500] Route_best = zeros(iter_max,n); % 各代最佳路径 Length_best = zeros(iter_max,1); % 各代最佳路径的长度 Length_ave = zeros(iter_max,1); % 各代路径的平均长度 Limit_iter = 0; % 程序收敛时迭代次数 %% 迭代寻找最佳路径 while iter <= iter_max % 随机产生各个蚂蚁的起点城市 start = zeros(m,1); for i = 1:m temp = randperm(n); %randperm函数打乱顺序 1-n随机排序 start = temp(1); end Table(:,1) = start; %路径记录表 % 构建解空间 citys_index = 1:n; % 逐个蚂蚁路径选择 for i =1:m % 逐个城市路径选择 for j = 2:n tabu = Table(i,1:(j - 1)); % 已访问的城市集合(禁忌表) allow_index = ~ismember(citys_index,tabu); % 1.ismember函数判断一个变量中的元素是否在另一个变量中出现,返回0-1矩阵; allow = citys_index(allow_index); % 待访问的城市集合 P = allow; % 计算城市间转移概率 for k = 1:length(allow) P(k) = Tau(tabu(end),allow(k))^alpha * Heu_F(tabu(end),allow(k))^beta; %线路选择概率的分子 end P = P / sum(P); %线路选择概率的分母 % 轮盘赌法选择下一个访问城市 Pc = cumsum(P); %cumsum函数用于求变量中累加元素的和,如A=[1,2,3,4,5],那么cumsum(A)=[1,3,6,10,15] target_index = find(Pc >= rand); target = allow(target_index(1)); Table(i,j) = target; end end % 计算各个蚂蚁的路径距离 Length = zeros(m,1); for i = 1:m Route = Table(i,:); for j = 1:(n - 1) Length(i) = Length(i) + D(Route(j),Route(j + 1)); end Length(i) = Length(i) + D(Route(n),Route(1)); %最后回到起点 end % 计算最短路径距离及平均距离 if iter == 1 [min_Length, min_index] = min(Length); Length_best(iter) = min_Length; Length_ave(iter) = mean(Length); Route_best(iter,:) = Table(min_index,:); Limit_iter = 1; else [min_Length,min_index] = min(Length); Length_best(iter) = min(Length_best(iter - 1),min_Length); Length_ave(iter) = mean(Length); if Length_best(iter) == min_Length Route_best(iter,:) = Table(min_index,:); Limit_iter = iter; else Route_best(iter,:) = Route_best((iter - 1),:); end end % 更新信息素 Delta_Tau = zeros(n,n); %信息素增量 % 逐个蚂蚁计算 for i = 1:m % 逐个城市计算 for j = 1:(n - 1) Delta_Tau(Table(i,j),Table(i,j+1)) = Delta_Tau(Table(i,j),Table(i,j+1)) + Q/Length(i); %Q为常数 end Delta_Tau(Table(i,n),Table(i,1)) = Delta_Tau(Table(i,n),Table(i,1)) + Q/Length(i); %最后回到第一个城市的最终值 end Tau = (1 - vol) * Tau + Delta_Tau; %信息素挥发损失的剩下部分+新的增量 % 迭代次数加1,清空路径记录表 iter = iter + 1; Table = zeros(m,n); end %% 结果显示 [Shortest_Length,index] = min(Length_best); Shortest_Route = Route_best(index,:); Time_Cost = etime(clock,t0); disp(['最短距离:' num2str(Shortest_Length)]); disp(['最短路径:' num2str( [Shortest_Route Shortest_Route(1)] )]); disp(['收敛迭代次数:' num2str(Limit_iter)]); disp(['程序执行时间:' num2str(Time_Cost),'秒']); %% 绘图 figure(2) hold on; plot([ city2(Shortest_Route,1);city2(Shortest_Route(1),1) ], [ city2(Shortest_Route,2);city2(Shortest_Route(1),2) ], 'r.-','Markersize',20); set(gca,'LineWidth',1.5); %边框加粗,美观 grid on; for i = 1:size(city2,1) text(city2(i,1),city2(i,2),[' ' num2str(i)]); end xlabel('城市位置横坐标'); ylabel('城市位置纵坐标'); title(['ACA最优化路径(最短距离:' num2str(Shortest_Length) ')']); hold off figure(3); %收敛图 subplot(1,3,2); plot(1:iter_max,Length_best,'b'); set(gca,'LineWidth',1.5); %边框加粗,美观 legend('最短距离'); xlabel('迭代次数'); ylabel('距离'); title('算法收敛轨迹'); set(gca,'LineWidth',1.5); %边框加粗,美观 %% 第三个聚类群 % 程序运行计时开始 t0 = clock; %% 计算城市间距离 n = size(city3,1)-1; %城市数 起点,终点同一个要减1 D = zeros(n,n); for i = 1:n for j = 1:n if i ~= j D(i,j) = sqrt(sum( ( city3(i,:) - city3(j,:) ).^2 ) ); %两点之间的距离 else D(i,j) = 1e-4; %为保证启发函数的分母不为0,设定的对角矩阵修正值为一个较小正值 end end end %% 初始化参数 m = 27+1; % 蚂蚁数量最好接近城市数量的1.5倍 alpha = 1; % 信息素重要程度因子[1,4]最好 beta = 5; % 启发函数重要程度因子 5最好 vol = 0.2; % 信息素挥发(volatilization)因子 Q = 10; % 常系数 Heu_F = 1./D; % 启发函数(heuristic function) Tau = ones(n,n); % 信息素矩阵 Table = zeros(n,n); % 路径记录表 iter = 1; % 迭代次数初值 iter_max = 300; % 最大迭代次数 [100,500] Route_best = zeros(iter_max,n); % 各代最佳路径 Length_best = zeros(iter_max,1); % 各代最佳路径的长度 Length_ave = zeros(iter_max,1); % 各代路径的平均长度 Limit_iter = 0; % 程序收敛时迭代次数 %% 迭代寻找最佳路径 while iter <= iter_max % 随机产生各个蚂蚁的起点城市 start = zeros(m,1); for i = 1:m temp = randperm(n); %randperm函数打乱顺序 1-n随机排序 start = temp(1); end Table(:,1) = start; %路径记录表 % 构建解空间 citys_index = 1:n; % 逐个蚂蚁路径选择 for i =1:m % 逐个城市路径选择 for j = 2:n tabu = Table(i,1:(j - 1)); % 已访问的城市集合(禁忌表) allow_index = ~ismember(citys_index,tabu); % 1.ismember函数判断一个变量中的元素是否在另一个变量中出现,返回0-1矩阵; allow = citys_index(allow_index); % 待访问的城市集合 P = allow; % 计算城市间转移概率 for k = 1:length(allow) P(k) = Tau(tabu(end),allow(k))^alpha * Heu_F(tabu(end),allow(k))^beta; %线路选择概率的分子 end P = P / sum(P); %线路选择概率的分母 % 轮盘赌法选择下一个访问城市 Pc = cumsum(P); %cumsum函数用于求变量中累加元素的和,如A=[1,2,3,4,5],那么cumsum(A)=[1,3,6,10,15] target_index = find(Pc >= rand); target = allow(target_index(1)); Table(i,j) = target; end end % 计算各个蚂蚁的路径距离 Length = zeros(m,1); for i = 1:m Route = Table(i,:); for j = 1:(n - 1) Length(i) = Length(i) + D(Route(j),Route(j + 1)); end Length(i) = Length(i) + D(Route(n),Route(1)); %最后回到起点 end % 计算最短路径距离及平均距离 if iter == 1 [min_Length, min_index] = min(Length); Length_best(iter) = min_Length; Length_ave(iter) = mean(Length); Route_best(iter,:) = Table(min_index,:); Limit_iter = 1; else [min_Length,min_index] = min(Length); Length_best(iter) = min(Length_best(iter - 1),min_Length); Length_ave(iter) = mean(Length); if Length_best(iter) == min_Length Route_best(iter,:) = Table(min_index,:); Limit_iter = iter; else Route_best(iter,:) = Route_best((iter - 1),:); end end % 更新信息素 Delta_Tau = zeros(n,n); %信息素增量 % 逐个蚂蚁计算 for i = 1:m % 逐个城市计算 for j = 1:(n - 1) Delta_Tau(Table(i,j),Table(i,j+1)) = Delta_Tau(Table(i,j),Table(i,j+1)) + Q/Length(i); %Q为常数 end Delta_Tau(Table(i,n),Table(i,1)) = Delta_Tau(Table(i,n),Table(i,1)) + Q/Length(i); %最后回到第一个城市的最终值 end Tau = (1 - vol) * Tau + Delta_Tau; %信息素挥发损失的剩下部分+新的增量 % 迭代次数加1,清空路径记录表 iter = iter + 1; Table = zeros(m,n); end %% 结果显示 [Shortest_Length,index] = min(Length_best); Shortest_Route = Route_best(index,:); Time_Cost = etime(clock,t0); disp(['最短距离:' num2str(Shortest_Length)]); disp(['最短路径:' num2str( [Shortest_Route Shortest_Route(1)] )]); disp(['收敛迭代次数:' num2str(Limit_iter)]); disp(['程序执行时间:' num2str(Time_Cost),'秒']); %% 绘图 figure(2) hold on; plot([ city3(Shortest_Route,1);city3(Shortest_Route(1),1) ], [ city3(Shortest_Route,2);city3(Shortest_Route(1),2) ], 'b.-','Markersize',20); set(gca,'LineWidth',1.5); %边框加粗,美观 grid on; for i = 1:size(city3,1) text(city3(i,1),city3(i,2),[' ' num2str(i)]); end xlabel('城市位置横坐标'); ylabel('城市位置纵坐标'); title(['ACA最优化路径(最短距离:' num2str(Shortest_Length) ')']); hold off axis([0 115 0 140]); %使得figure(2) 画布尺寸为100*120 figure(3); %收敛图 subplot(1,3,3); plot(1:iter_max,Length_best,'b'); set(gca,'LineWidth',1.5); %边框加粗,美观 legend('最短距离'); xlabel('迭代次数'); ylabel('距离'); title('算法收敛轨迹'); set(gca,'LineWidth',1.5); %边框加粗,美观
代码改进
三处m值 改为
m = size(city1,1) -1;
m = size(city2,1) -1;
m = size(city3,1) -1;
避免维度错误
首先通过kmean(python)进行聚类,按无人机数量要求进行分类
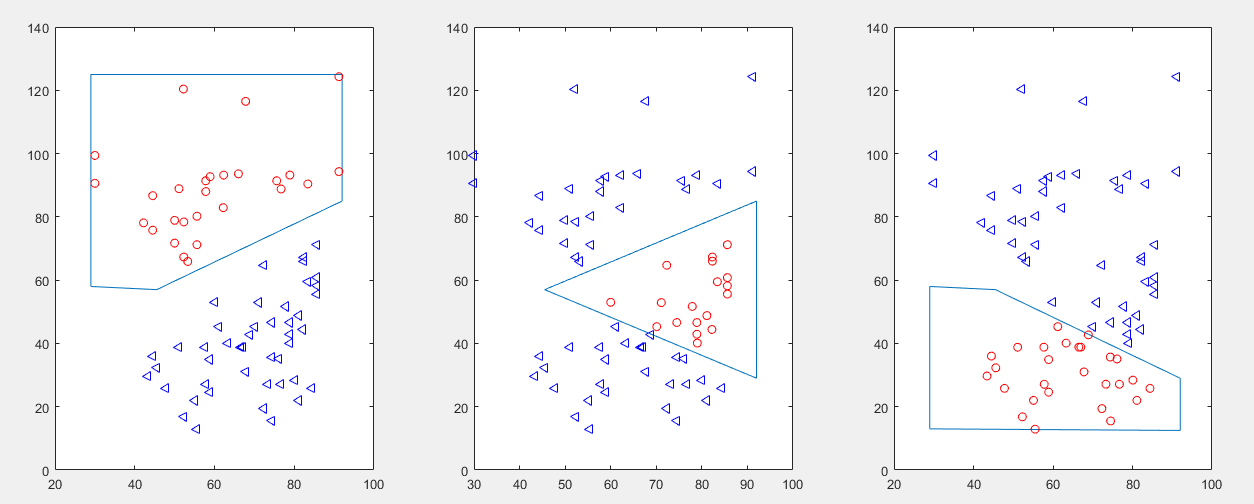
将聚类好的位置数据分别存入city1,city2,city3中分别应用蚁群算法进行TSP运算
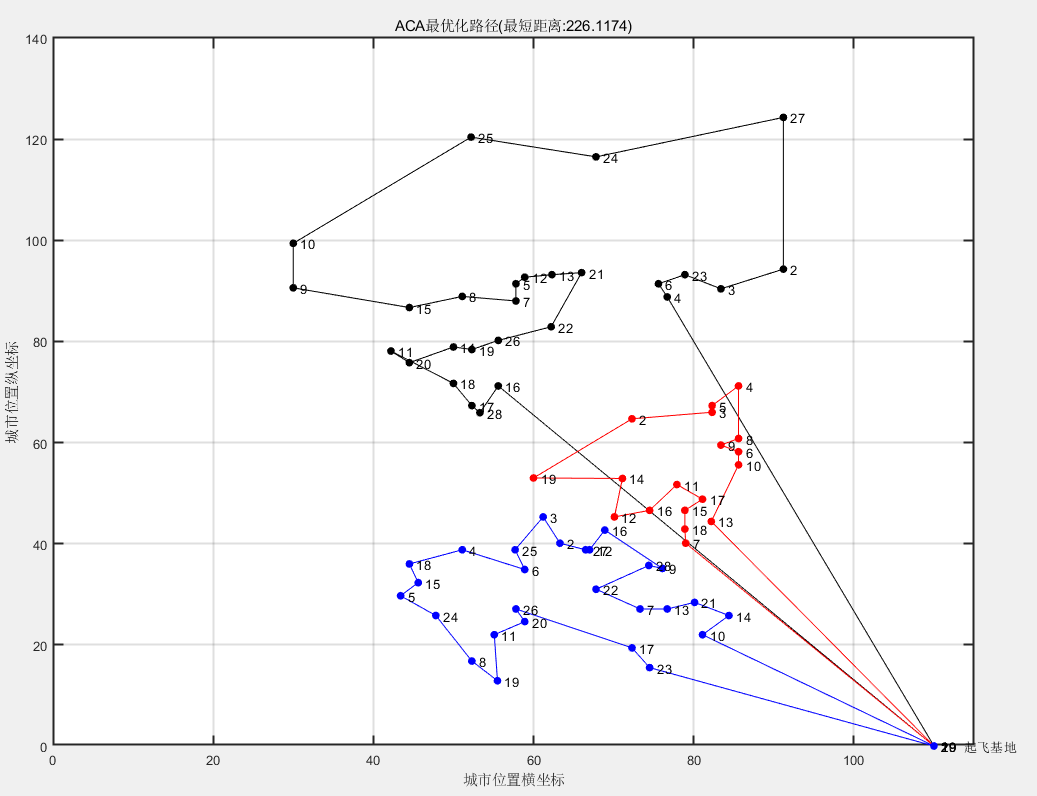
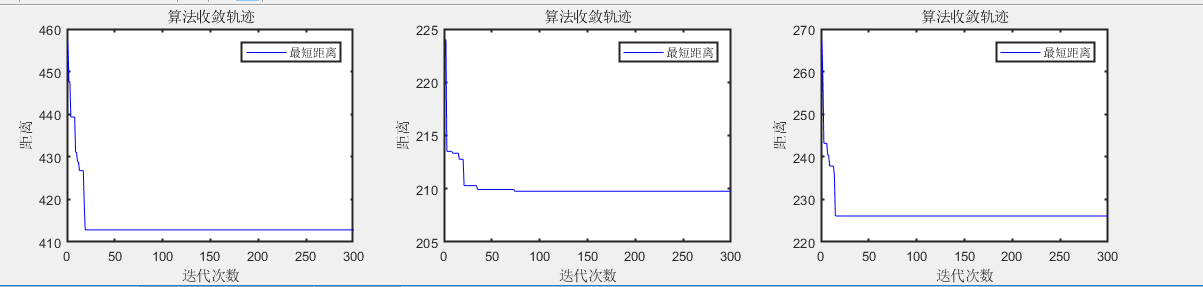
缺点是由于没有考虑起点的距离 这里聚类应用不是特别好 导致上部分的路程较大 几乎是蓝红的两倍
最短距离:412.8601
最短路径:4 6 23 3 2 27 24 25 10 9 15 8 7 5 12 13 21 22 26 19 14 20 11 18 17 28 16 1 4
最短距离:209.7699
最短路径:7 18 15 17 11 16 12 14 19 2 3 5 4 8 9 6 10 13 1 7
最短距离:226.1174
最短路径:10 14 21 13 7 22 28 9 16 12 27 2 3 25 6 4 18 15 5 24 8 19 11 20 26 17 23 1 10
需要改进

%% 数据准备 % 清空环境变量 clear all; clc; citys = xlsread('c:UsersclementeDesktop erminal.xlsx','B2:C73'); ab1= [91 27.6 27.08 91]; % 五边形各点横坐标 最后回到第一个点 形成闭环 cd1= [13 10.1 107.77 13]; % 五边形各点纵坐标 最后回到第一个点 形成闭环 ab2= [91 27.08 53.7 91]; % 三角形各点横坐标 最后回到第一个点 形成闭环 cd2= [13 107.77 129.4 13]; % 三角形各点纵坐标 最后回到第一个点 形成闭环 ab3= [91 53.7 93.8 91]; % 五边形各点横坐标 最后回到第一个点 形成闭环 cd3= [13 129.4 129.1 13]; % 五边形各点纵坐标 最后回到第一个点 形成闭环 x=citys(:,1); y=citys(:,2); in1=inpolygon(x,y,ab1,cd1); in2=inpolygon(x,y,ab2,cd2); in3=inpolygon(x,y,ab3,cd3); figure(1); subplot(1,3,1); plot(ab1,cd1,x(in1),y(in1),'ro',x(~in1),y(~in1),'b<') subplot(1,3,2); plot(ab2,cd2,x(in2),y(in2),'ro',x(~in2),y(~in2),'b<') subplot(1,3,3); plot(ab3,cd3,x(in3),y(in3),'ro',x(~in3),y(~in3),'b<') city1=citys(in1,:); city2=citys(in2,:); city3=citys(in3,:); basepoint=[110 0]; %无人机出发 基地的坐标 city1=[basepoint;city1;basepoint]; %基地加入到第一个聚类区域 city2=[basepoint;city2;basepoint]; %基地加入到第二个聚类区域 city3=[basepoint;city3;basepoint]; %基地加入到第三个聚类区域 %% 第一个聚类群 % 程序运行计时开始 t0 = clock; %% 计算城市间距离 n = size(city1,1) -1; %城市数 起点,终点同一个要减1 D = zeros(n,n); for i = 1:n for j = 1:n if i ~= j D(i,j) = sqrt(sum( ( city1(i,:) - city1(j,:) ).^2 ) ); %两点之间的距离 else D(i,j) = 1e-4; %为保证启发函数的分母不为0,设定的对角矩阵修正值为一个较小正值 end end end %% 初始化参数 m = size(city1,1) -1; % 蚂蚁数量最好接近城市数量的1.5倍 +1是因为新加入了基地 alpha = 1; % 信息素重要程度因子[1,4]最好 beta = 5; % 启发函数重要程度因子 5最好 vol = 0.2; % 信息素挥发(volatilization)因子 Q = 10; % 常系数 Heu_F = 1./D; % 启发函数(heuristic function) Tau = ones(n,n); % 信息素矩阵 Table = zeros(n,n); % 路径记录表 iter = 1; % 迭代次数初值 iter_max = 300; % 最大迭代次数 [100,500] Route_best = zeros(iter_max,n); % 各代最佳路径 Length_best = zeros(iter_max,1); % 各代最佳路径的长度 Length_ave = zeros(iter_max,1); % 各代路径的平均长度 Limit_iter = 0; % 程序收敛时迭代次数 %% 迭代寻找最佳路径 while iter <= iter_max % 随机产生各个蚂蚁的起点城市 start = zeros(m,1); for i = 1:m temp = randperm(n); %randperm函数打乱顺序 1-n随机排序 start = temp(1); end Table(:,1) = start; %路径记录表 % 构建解空间 citys_index = 1:n; % 逐个蚂蚁路径选择 for i =1:m % 逐个城市路径选择 for j = 2:n tabu = Table(i,1:(j - 1)); % 已访问的城市集合(禁忌表) allow_index = ~ismember(citys_index,tabu); % 1.ismember函数判断一个变量中的元素是否在另一个变量中出现,返回0-1矩阵; allow = citys_index(allow_index); % 待访问的城市集合 P = allow; % 计算城市间转移概率 for k = 1:length(allow) P(k) = Tau(tabu(end),allow(k))^alpha * Heu_F(tabu(end),allow(k))^beta; %线路选择概率的分子 end P = P / sum(P); %线路选择概率的分母 % 轮盘赌法选择下一个访问城市 Pc = cumsum(P); %cumsum函数用于求变量中累加元素的和,如A=[1,2,3,4,5],那么cumsum(A)=[1,3,6,10,15] target_index = find(Pc >= rand); target = allow(target_index(1)); Table(i,j) = target; end end % 计算各个蚂蚁的路径距离 Length = zeros(m,1); for i = 1:m Route = Table(i,:); for j = 1:(n - 1) Length(i) = Length(i) + D(Route(j),Route(j + 1)); end Length(i) = Length(i) + D(Route(n),Route(1)); %最后回到起点 end % 计算最短路径距离及平均距离 if iter == 1 [min_Length, min_index] = min(Length); Length_best(iter) = min_Length; Length_ave(iter) = mean(Length); Route_best(iter,:) = Table(min_index,:); Limit_iter = 1; else [min_Length,min_index] = min(Length); Length_best(iter) = min(Length_best(iter - 1),min_Length); Length_ave(iter) = mean(Length); if Length_best(iter) == min_Length Route_best(iter,:) = Table(min_index,:); Limit_iter = iter; else Route_best(iter,:) = Route_best((iter - 1),:); end end % 更新信息素 Delta_Tau = zeros(n,n); %信息素增量 % 逐个蚂蚁计算 for i = 1:m % 逐个城市计算 for j = 1:(n - 1) Delta_Tau(Table(i,j),Table(i,j+1)) = Delta_Tau(Table(i,j),Table(i,j+1)) + Q/Length(i); %Q为常数 end Delta_Tau(Table(i,n),Table(i,1)) = Delta_Tau(Table(i,n),Table(i,1)) + Q/Length(i); %最后回到第一个城市的最终值 end Tau = (1 - vol) * Tau + Delta_Tau; %信息素挥发损失的剩下部分+新的增量 % 迭代次数加1,清空路径记录表 iter = iter + 1; Table = zeros(m,n); end %% 结果显示 [Shortest_Length,index] = min(Length_best); Shortest_Route = Route_best(index,:); Time_Cost = etime(clock,t0); disp(['最短距离:' num2str(Shortest_Length)]); disp(['最短路径:' num2str( [Shortest_Route Shortest_Route(1)] )]); disp(['收敛迭代次数:' num2str(Limit_iter)]); disp(['程序执行时间:' num2str(Time_Cost),'秒']); %% 绘图 figure(2) plot([ city1(Shortest_Route,1);city1(Shortest_Route(1),1) ], [ city1(Shortest_Route,2);city1(Shortest_Route(1),2) ], 'k.-','Markersize',20); set(gca,'LineWidth',1.5); %边框加粗,美观 grid on; for i = 1:size(city1,1) text(city1(i,1),city1(i,2),[' ' num2str(i)]); end text(city1(1,1),city1(1,2),' 起飞基地'); xlabel('城市位置横坐标'); ylabel('城市位置纵坐标'); title(['ACA最优化路径(最短距离:' num2str(Shortest_Length) ')']); figure(3); %收敛图 subplot(1,3,1); plot(1:iter_max,Length_best,'b'); set(gca,'LineWidth',1.5); %边框加粗,美观 legend('最短距离'); xlabel('迭代次数'); ylabel('距离'); title('算法收敛轨迹'); set(gca,'LineWidth',1.5); %边框加粗,美观 %% 第二个聚类群 % 程序运行计时开始 t0 = clock; %% 计算城市间距离 n = size(city2,1)-1; %城市数 起点,终点同一个要减1 D = zeros(n,n); for i = 1:n for j = 1:n if i ~= j D(i,j) = sqrt(sum( ( city2(i,:) - city2(j,:) ).^2 ) ); %两点之间的距离 else D(i,j) = 1e-4; %为保证启发函数的分母不为0,设定的对角矩阵修正值为一个较小正值 end end end %% 初始化参数 m = size(city2,1) -1; % 蚂蚁数量最好接近城市数量的1.5倍 alpha = 1; % 信息素重要程度因子[1,4]最好 beta = 5; % 启发函数重要程度因子 5最好 vol = 0.2; % 信息素挥发(volatilization)因子 Q = 10; % 常系数 Heu_F = 1./D; % 启发函数(heuristic function) Tau = ones(n,n); % 信息素矩阵 Table = zeros(n,n); % 路径记录表 iter = 1; % 迭代次数初值 iter_max = 300; % 最大迭代次数 [100,500] Route_best = zeros(iter_max,n); % 各代最佳路径 Length_best = zeros(iter_max,1); % 各代最佳路径的长度 Length_ave = zeros(iter_max,1); % 各代路径的平均长度 Limit_iter = 0; % 程序收敛时迭代次数 %% 迭代寻找最佳路径 while iter <= iter_max % 随机产生各个蚂蚁的起点城市 start = zeros(m,1); for i = 1:m temp = randperm(n); %randperm函数打乱顺序 1-n随机排序 start = temp(1); end Table(:,1) = start; %路径记录表 % 构建解空间 citys_index = 1:n; % 逐个蚂蚁路径选择 for i =1:m % 逐个城市路径选择 for j = 2:n tabu = Table(i,1:(j - 1)); % 已访问的城市集合(禁忌表) allow_index = ~ismember(citys_index,tabu); % 1.ismember函数判断一个变量中的元素是否在另一个变量中出现,返回0-1矩阵; allow = citys_index(allow_index); % 待访问的城市集合 P = allow; % 计算城市间转移概率 for k = 1:length(allow) P(k) = Tau(tabu(end),allow(k))^alpha * Heu_F(tabu(end),allow(k))^beta; %线路选择概率的分子 end P = P / sum(P); %线路选择概率的分母 % 轮盘赌法选择下一个访问城市 Pc = cumsum(P); %cumsum函数用于求变量中累加元素的和,如A=[1,2,3,4,5],那么cumsum(A)=[1,3,6,10,15] target_index = find(Pc >= rand); target = allow(target_index(1)); Table(i,j) = target; end end % 计算各个蚂蚁的路径距离 Length = zeros(m,1); for i = 1:m Route = Table(i,:); for j = 1:(n - 1) Length(i) = Length(i) + D(Route(j),Route(j + 1)); end Length(i) = Length(i) + D(Route(n),Route(1)); %最后回到起点 end % 计算最短路径距离及平均距离 if iter == 1 [min_Length, min_index] = min(Length); Length_best(iter) = min_Length; Length_ave(iter) = mean(Length); Route_best(iter,:) = Table(min_index,:); Limit_iter = 1; else [min_Length,min_index] = min(Length); Length_best(iter) = min(Length_best(iter - 1),min_Length); Length_ave(iter) = mean(Length); if Length_best(iter) == min_Length Route_best(iter,:) = Table(min_index,:); Limit_iter = iter; else Route_best(iter,:) = Route_best((iter - 1),:); end end % 更新信息素 Delta_Tau = zeros(n,n); %信息素增量 % 逐个蚂蚁计算 for i = 1:m % 逐个城市计算 for j = 1:(n - 1) Delta_Tau(Table(i,j),Table(i,j+1)) = Delta_Tau(Table(i,j),Table(i,j+1)) + Q/Length(i); %Q为常数 end Delta_Tau(Table(i,n),Table(i,1)) = Delta_Tau(Table(i,n),Table(i,1)) + Q/Length(i); %最后回到第一个城市的最终值 end Tau = (1 - vol) * Tau + Delta_Tau; %信息素挥发损失的剩下部分+新的增量 % 迭代次数加1,清空路径记录表 iter = iter + 1; Table = zeros(m,n); end %% 结果显示 [Shortest_Length,index] = min(Length_best); Shortest_Route = Route_best(index,:); Time_Cost = etime(clock,t0); disp(['最短距离:' num2str(Shortest_Length)]); disp(['最短路径:' num2str( [Shortest_Route Shortest_Route(1)] )]); disp(['收敛迭代次数:' num2str(Limit_iter)]); disp(['程序执行时间:' num2str(Time_Cost),'秒']); %% 绘图 figure(2) hold on; plot([ city2(Shortest_Route,1);city2(Shortest_Route(1),1) ], [ city2(Shortest_Route,2);city2(Shortest_Route(1),2) ], 'r.-','Markersize',20); set(gca,'LineWidth',1.5); %边框加粗,美观 grid on; for i = 1:size(city2,1) text(city2(i,1),city2(i,2),[' ' num2str(i)]); end xlabel('城市位置横坐标'); ylabel('城市位置纵坐标'); title(['ACA最优化路径(最短距离:' num2str(Shortest_Length) ')']); hold off figure(3); %收敛图 subplot(1,3,2); plot(1:iter_max,Length_best,'b'); set(gca,'LineWidth',1.5); %边框加粗,美观 legend('最短距离'); xlabel('迭代次数'); ylabel('距离'); title('算法收敛轨迹'); set(gca,'LineWidth',1.5); %边框加粗,美观 %% 第三个聚类群 % 程序运行计时开始 t0 = clock; %% 计算城市间距离 n = size(city3,1)-1; %城市数 起点,终点同一个要减1 D = zeros(n,n); for i = 1:n for j = 1:n if i ~= j D(i,j) = sqrt(sum( ( city3(i,:) - city3(j,:) ).^2 ) ); %两点之间的距离 else D(i,j) = 1e-4; %为保证启发函数的分母不为0,设定的对角矩阵修正值为一个较小正值 end end end %% 初始化参数 m = size(city3,1) -1; % 蚂蚁数量最好接近城市数量的1.5倍 alpha = 1; % 信息素重要程度因子[1,4]最好 beta = 5; % 启发函数重要程度因子 5最好 vol = 0.2; % 信息素挥发(volatilization)因子 Q = 10; % 常系数 Heu_F = 1./D; % 启发函数(heuristic function) Tau = ones(n,n); % 信息素矩阵 Table = zeros(n,n); % 路径记录表 iter = 1; % 迭代次数初值 iter_max = 300; % 最大迭代次数 [100,500] Route_best = zeros(iter_max,n); % 各代最佳路径 Length_best = zeros(iter_max,1); % 各代最佳路径的长度 Length_ave = zeros(iter_max,1); % 各代路径的平均长度 Limit_iter = 0; % 程序收敛时迭代次数 %% 迭代寻找最佳路径 while iter <= iter_max % 随机产生各个蚂蚁的起点城市 start = zeros(m,1); for i = 1:m temp = randperm(n); %randperm函数打乱顺序 1-n随机排序 start = temp(1); end Table(:,1) = start; %路径记录表 % 构建解空间 citys_index = 1:n; % 逐个蚂蚁路径选择 for i =1:m % 逐个城市路径选择 for j = 2:n tabu = Table(i,1:(j - 1)); % 已访问的城市集合(禁忌表) allow_index = ~ismember(citys_index,tabu); % 1.ismember函数判断一个变量中的元素是否在另一个变量中出现,返回0-1矩阵; allow = citys_index(allow_index); % 待访问的城市集合 P = allow; % 计算城市间转移概率 for k = 1:length(allow) P(k) = Tau(tabu(end),allow(k))^alpha * Heu_F(tabu(end),allow(k))^beta; %线路选择概率的分子 end P = P / sum(P); %线路选择概率的分母 % 轮盘赌法选择下一个访问城市 Pc = cumsum(P); %cumsum函数用于求变量中累加元素的和,如A=[1,2,3,4,5],那么cumsum(A)=[1,3,6,10,15] target_index = find(Pc >= rand); target = allow(target_index(1)); Table(i,j) = target; end end % 计算各个蚂蚁的路径距离 Length = zeros(m,1); for i = 1:m Route = Table(i,:); for j = 1:(n - 1) Length(i) = Length(i) + D(Route(j),Route(j + 1)); end Length(i) = Length(i) + D(Route(n),Route(1)); %最后回到起点 end % 计算最短路径距离及平均距离 if iter == 1 [min_Length, min_index] = min(Length); Length_best(iter) = min_Length; Length_ave(iter) = mean(Length); Route_best(iter,:) = Table(min_index,:); Limit_iter = 1; else [min_Length,min_index] = min(Length); Length_best(iter) = min(Length_best(iter - 1),min_Length); Length_ave(iter) = mean(Length); if Length_best(iter) == min_Length Route_best(iter,:) = Table(min_index,:); Limit_iter = iter; else Route_best(iter,:) = Route_best((iter - 1),:); end end % 更新信息素 Delta_Tau = zeros(n,n); %信息素增量 % 逐个蚂蚁计算 for i = 1:m % 逐个城市计算 for j = 1:(n - 1) Delta_Tau(Table(i,j),Table(i,j+1)) = Delta_Tau(Table(i,j),Table(i,j+1)) + Q/Length(i); %Q为常数 end Delta_Tau(Table(i,n),Table(i,1)) = Delta_Tau(Table(i,n),Table(i,1)) + Q/Length(i); %最后回到第一个城市的最终值 end Tau = (1 - vol) * Tau + Delta_Tau; %信息素挥发损失的剩下部分+新的增量 % 迭代次数加1,清空路径记录表 iter = iter + 1; Table = zeros(m,n); end %% 结果显示 [Shortest_Length,index] = min(Length_best); Shortest_Route = Route_best(index,:); Time_Cost = etime(clock,t0); disp(['最短距离:' num2str(Shortest_Length)]); disp(['最短路径:' num2str( [Shortest_Route Shortest_Route(1)] )]); disp(['收敛迭代次数:' num2str(Limit_iter)]); disp(['程序执行时间:' num2str(Time_Cost),'秒']); %% 绘图 figure(2) hold on; plot([ city3(Shortest_Route,1);city3(Shortest_Route(1),1) ], [ city3(Shortest_Route,2);city3(Shortest_Route(1),2) ], 'b.-','Markersize',20); set(gca,'LineWidth',1.5); %边框加粗,美观 grid on; for i = 1:size(city3,1) text(city3(i,1),city3(i,2),[' ' num2str(i)]); end xlabel('城市位置横坐标'); ylabel('城市位置纵坐标'); title(['ACA最优化路径(最短距离:' num2str(Shortest_Length) ')']); hold off axis([0 115 0 140]); %使得figure(2) 画布尺寸为100*120 figure(3); %收敛图 subplot(1,3,3); plot(1:iter_max,Length_best,'b'); set(gca,'LineWidth',1.5); %边框加粗,美观 legend('最短距离'); xlabel('迭代次数'); ylabel('距离'); title('算法收敛轨迹'); set(gca,'LineWidth',1.5); %边框加粗,美观
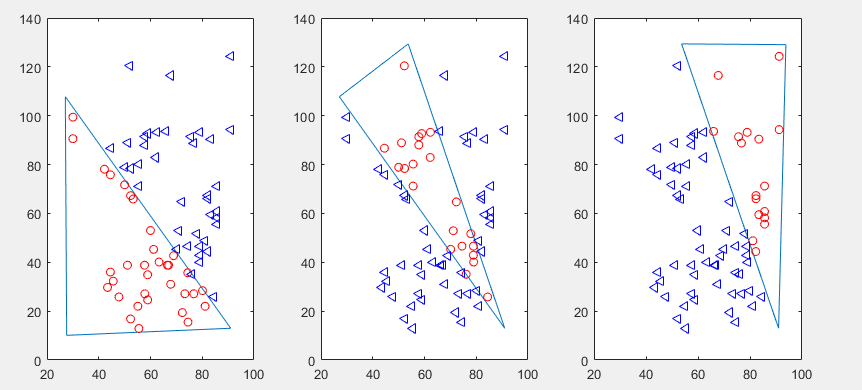
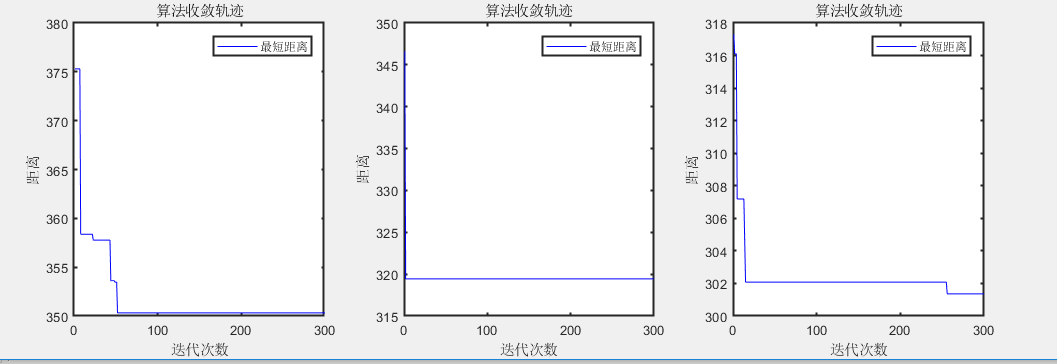
最短距离:350.3253
最短路径:15 25 18 13 26 17 32 5 7 33 30 6 8 11 4 2 3 9 22 19 10 28 16 14 23 24 31 12 29 20 34 21 27 1 15
收敛迭代次数:204
程序执行时间:5.667秒
最短距离:319.4375
最短路径:5 2 3 4 8 7 14 21 9 10 16 22 12 18 23 11 17 19 1 13 15 6 20 5
收敛迭代次数:2
程序执行时间:2.288秒
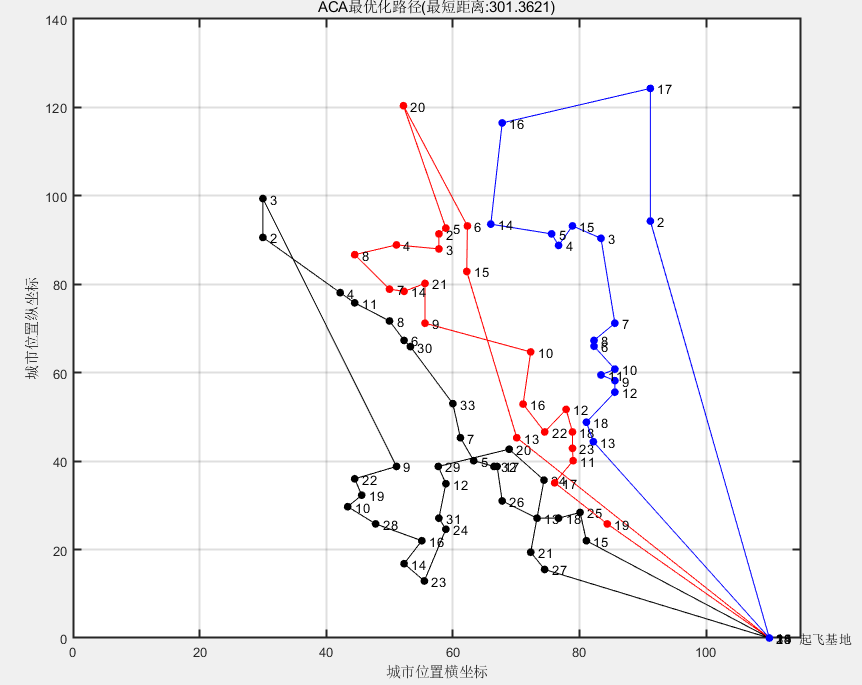
最短距离:301.3621
最短路径:17 16 14 5 4 15 3 7 8 6 10 11 9 12 18 13 1 2 17
收敛迭代次数:256
程序执行时间:1.324秒
还是与最优化差距较大
下一步考虑改进 近距离的点合并
