Given a sequence of integers a1, ..., an andq queries x1, ..., xq on it. For each queryxi you have to count the number of pairs(l, r) such that 1 ≤ l ≤ r ≤ n and gcd(al, al + 1, ..., ar) = xi.
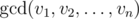 is a greatest common divisor ofv1, v2, ..., vn,
that is equal to a largest positive integer that divides allvi.
is a greatest common divisor ofv1, v2, ..., vn,
that is equal to a largest positive integer that divides allvi.
The first line of the input contains integer n, (1 ≤ n ≤ 105), denoting the length of the sequence. The next line containsn space separated integers a1, ..., an, (1 ≤ ai ≤ 109).
The third line of the input contains integer q, (1 ≤ q ≤ 3 × 105), denoting the number of queries. Then followsq lines, each contain an integer xi, (1 ≤ xi ≤ 109).
For each query print the result in a separate line.
3 2 6 3 5 1 2 3 4 6
1 2 2 0 1
7 10 20 3 15 1000 60 16 10 1 2 3 4 5 6 10 20 60 1000
14 0 2 2 2 0 2 2 1 1
题意给你一个序列和q个询问,输出有多少个区间[l,r]满足区间gcd为询问的值。
思路:处理出每一个区间的gcd(要注意合并区间),假设有询问则直接加上去。
#include <bits/stdc++.h>
using namespace std;
std::map<int, int> id;
vector<pair<int,int> >gcdList;
const int MAXN=100000+5;
int query[MAXN*3],A[MAXN];
long long ans[MAXN*3];
int _gcd(int a,int b){return b?_gcd(b,a%b):a;}
int ID(int x){
if(!id[x])id[x]=id.size();
return id[x];
}
int main(int argc, char const *argv[])
{
int n;
ios_base::sync_with_stdio(false);
gcdList.clear();id.clear();
cin>>n;
for(int i=1;i<=n;i++)cin>>A[i];
int q;cin>>q;
for(int i=1;i<=q;i++){
cin>>query[i];
query[i]=ID(query[i]);
}
for(int i=1;i<=n;i++){
for(int j=0;j<gcdList.size();j++)
gcdList[j].first=_gcd(gcdList[j].first,A[i]);
gcdList.push_back(make_pair(A[i],i));
int cnt=1;
//sort(gcdList.begin(), gcdList.end());
for(int j=1;j<gcdList.size();j++){
if(gcdList[j].first!=gcdList[cnt-1].first)
gcdList[cnt++]=gcdList[j];
}
gcdList.resize(cnt);
for(int j=0;j<gcdList.size();j++){
if(id[gcdList[j].first]){
int r=i+1;
if(j+1<gcdList.size())r=gcdList[j+1].second;
ans[id[gcdList[j].first]]+=r-gcdList[j].second;
}
}
}
for(int i=1;i<=q;i++)cout<<ans[query[i]]<<endl;
return 0;
}