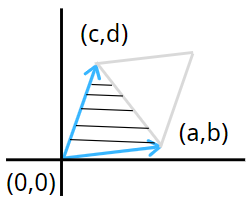本节将讲解行列式的应用。
从行列式出发,又可以发现新的公式。
逆矩阵公式
公式
(2*2) 的逆矩阵公式
[{left(
�egin{array}{cc}
a & b \
c & d \
end{array}
ight)}^{-1}=frac{1}{ ext{ad}- ext{bc}}left(
�egin{array}{cc}
d & -b \
-c & a \
end{array}
ight)
]
右侧第一项是行列式的倒数,第二项是原矩阵每一行的代数余子式构成的矩阵的转置,记为 (C^{T}) .她是原矩阵的伴随矩阵。伴随矩阵的各元素是原矩阵对应元素的代数余子式。
(n*n) 矩阵的逆矩阵公式
[A^{-1}=frac{1}{detA}C^{T}
]
(A) 的行列式由 (n) 个元素的乘积组成;伴随矩阵个元素由 (n-1) 个乘积组成。
高斯-若尔当求逆法在数值计算无懈可击。
现在我们得到了逆矩阵的代数表达式,使得算法能够写成代数形式。
值得注意的是,不建议用这个公式计算,毫无疑问消元法更有利于手算或计算机处理。
同时这个式子也告诉我们,只有当行列式不等于0时,才有逆矩阵。
证明
证明逆矩阵公式成立,我们可以证明 (AA^{-1}=I) 成立,即证明 (Afrac{C^{T}}{detA}=I)。
行列式是一个数,所以我们可以将她放在等式另一边:
[AC^{T}=(detA)I
]
注意,右边是行列式(一个数)乘以单位阵,结果是对角矩阵,不是一个数。
将左边展开
[left(
�egin{array}{cccc}
a_{11} & a_{12} & ... & a_{1 n} \
a_{21} & ... & ... & ... \
... & ... & ... & ... \
a_{ ext{n1}} & ... & ... & a_{ ext{nn}} \
end{array}
ight) left(
�egin{array}{cccc}
C_{11} & C_{21} & ... & C_{ ext{n1}} \
C_{12} & ... & ... & ... \
... & ... & ... & ... \
C_{1 n} & ... & ... & C_{ ext{nn}} \
end{array}
ight)
]
根据行列式的代数余子式公式
[detA=a_{i1}C_{i1}+a_{i2}C_{i2}+...a_{in}C_{in}
]
矩阵 (A) 的第 (i) 行乘以伴随矩阵的第 (i) 列,结果就是行列式 (detA).
故
[left(
�egin{array}{cccc}
a_{11} & a_{12} & ... & a_{1 n} \
a_{21} & ... & ... & ... \
... & ... & ... & ... \
a_{ ext{n1}} & ... & ... & a_{ ext{nn}} \
end{array}
ight) left(
�egin{array}{cccc}
C_{11} & C_{21} & ... & C_{ ext{n1}} \
C_{12} & ... & ... & ... \
... & ... & ... & ... \
C_{1 n} & ... & ... & C_{ ext{nn}} \
end{array}
ight)=
left(
�egin{array}{cccc}
ext{detA} & ... & ... & ... \
... & ext{detA} & ... & ... \
... & ... & ... & ... \
... & ... & ... & ext{detA} \
end{array}
ight)
]
对角线上都是 (detA).
那么结果的非对角线元素等于什么呢?
某一行乘以其他行的代数余子式,结果为0.
某一行乘以其他行的代数余子式,我们还是可以看作一个行列式,结果为0,表示可能这个行列式的其中两行相等。
以 (2*2) 矩阵为例
利用行列式的代数余子式求解
[{left|
�egin{array}{cc}
a & b \
c & d \
end{array}
ight|}=ad+b(-c)
]
如果第一行乘以第二行的代数余子式,则行列式等于:
[a(-b)+b(a)=0
]
这种情况和计算矩阵行列式有两行相等的情况一样,即
[{left|
�egin{array}{cc}
a & b \
a & b \
end{array}
ight|}=a(b)+b(-a)=0
]
这种情况同样适用在 (n*n) 矩阵。
(A) 的第一行,乘以最后一行的代数余子式,相当于求一个特殊矩阵的行列式,特殊矩阵的第一行和最后一行相等。
所以除了对角线上的元素,其余都是零。
[left(
�egin{array}{cccc}
a_{11} & a_{12} & ... & a_{1 n} \
a_{21} & ... & ... & ... \
... & ... & ... & ... \
a_{ ext{n1}} & ... & ... & a_{ ext{nn}} \
end{array}
ight) left(
�egin{array}{cccc}
C_{11} & C_{21} & ... & C_{ ext{n1}} \
C_{12} & ... & ... & ... \
... & ... & ... & ... \
C_{1 n} & ... & ... & C_{ ext{nn}} \
end{array}
ight)=
left(
�egin{array}{cccc}
ext{detA} & 0 & ... & 0\
0 & ext{detA} & ... & 0 \
... & ... & ... & ... \
0 & 0 & ... & ext{detA} \
end{array}
ight)
]
证得左边等于右边。
克莱姆法则
克莱姆法则是线代中一个关于求解线性方程组的定理。
假设 (Ax=b) ,则我们可以得到方程组的解
[x=A^{-1}x=frac{1}{detA}C^{T}b
]
其中,(C^{T}b) 是矩阵 (A) 的元素的代数余子式构成的矩阵,而 (b) 是一个向量,我们也可以把她们看成一个行列式,记为 (detB) .(B) 表示这个行列式的原矩阵。
[x=frac{detB}{detA}
]
克莱姆发现 (x) 的每个分量可以写为:
[x_i=frac{detB_i}{detA}
]
并且发现了 矩阵 (B_i) 的规律:
(B_1) 就是矩阵 (A) 的第一列用向量 (b) 代替;
(B_2) 就是矩阵 (A) 的第二列用向量 (b) 代替;
...
(B_i) 就是矩阵 (A) 的第 (i) 列用向量 (b) 代替。
以 (B_1) 为例说明
[B_1=left(
�egin{array}{cccc}
b_1 & a_{12} & square & a_{1 n} \
b_2 & a_{22} & square & a_{2 n} \
square & square & square & square \
b_n & a_{ ext{n2}} & square & a_{ ext{nn}} \
end{array}
ight)
]
求 (B_1) 的行列式,利用代数余子式公式,在第一行展开
[|B_1|=C_{11}b_1+C_{21}b_2+C_{31}b_3+...++C_{n1}b_n
]
可以看出,这其实就是 (C^{T}b) 的一部分。
(C) 是比原来小一阶的行列式,所以 (C) 包含矩阵 (A) 的 (n-1) 阶元素。
这就是克莱姆法则。
注意,同逆矩阵公式一样,不建议使用她计算,如果要用这个计算方程组的解,我们就需要计算 (n) 个(detB) ,非常麻烦。
克莱姆法则的价值在于她给出了求解线性方程组的代数表达式,而不只是能进行数值运算。
体积
这个课题是通过行列式求体积。
命题是:行列式的绝对值等于一个箱子的体积。
先看 (3*3) 情况

矩阵的第一行对应三维空间中一个向量,她是箱子的第一条边,矩阵的第二行对应箱子的第二条边,矩阵的第三行对应箱子的第三条边。
得到箱子的三条边,就能得到整个箱子的形状——平行六面体。
箱子由三条边固定。每个面都是平行四边形。
箱子的体积等于行列式的绝对值。因为行列式有可能是负数。
[V_{box}=|detA|
]
证明
行列式的三性质定义了行列式,所以我们证明箱子具有三性质,那么箱子就一定等于行列式,这是很巧妙的间接证明方法。
- 性质1是讲单位阵的。假设矩阵 (A) 是单位阵,则箱子是一个单位立方体。我们可以先证明单位立方体的体积等于行列式的绝对值。
单位矩阵的行列式值为1,单位立方体的值也为1,假设成立,证明性子具备性质1。
如果矩阵 (A) 是正交矩阵(Q) ,她的各列都是标准正交向量。 矩阵 (Q) 构成的箱子,与单位阵不同在于,箱子在空间被旋转了。怎么证明 (|Q|=±1)
(Q) 具有以下性质
[Q^TQ=I
]
两边同时取行列式
[�egin {align}
&det(Q^TQ)=1\
性质9
ightarrow&|Q^T||Q|=1\
性质10
ightarrow&|Q|^2=1
end {align}
]
故 (|Q|=±1) 。
性质1成立。
-
对于性质2是关于符号的,交换2行,很显然箱子的体积没有发生改变,我们不关心性质2。
-
那么长方体呢?
长方体的情况其实就是行乘以标量。
如果一行翻倍,体积也会翻倍。根据行列式的性质3a,可以把一行的公因数提出来,所以行列式也翻倍。
因此箱子的体积也满足行列式的性质3a。
那么性质3b呢
[left|
�egin{array}{cc}
a+a^{'} & b+b^{'} \
c & d \
end{array}
ight|=
left|
�egin{array}{cc}
a & b \
c & d \
end{array}
ight|+
left|
�egin{array}{cc}
a^{'} & b^{'} \
c & d \
end{array}
ight|
]
我们的目标是要求体积,但对于 (2*2) 情况,等于求面积

求平行四边形的面积,在以前就是底乘以高,但是我们就需要去计算底和高分别是多少,计算过程中可能有根号,比较麻烦。
对于 (2*2) 情况,平行四边形的面积等于对应矩阵的行列式的值。
[area quad of quad parallelogram={left|
�egin{array}{cc}
a & b \
c & d \
end{array}
ight|}=ad-bc
]
我们利用坐标值,就能通过行列式求出体积和面积。
三角形的面积是平行四边形面积的一半。
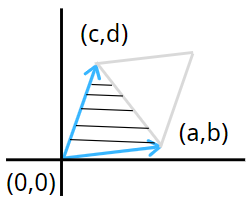
公式为
[area quad of quad triangle =frac{1}{2}(ad-bc)
]
再看三角形另一种情况,如果三角形的顶点不在原点上怎么办?

这个问题其实是让三角形面积公式一般化
[area quad of quad triangle =frac{1}{2}
left|
�egin{array}{ccc}
x_1 & y_1 & 1 \
x_2 & y_2 & 1 \
x_3 & y_3 & 1 \
end{array}
ight|
]