仙人掌&圆方树学习笔记
1、仙人掌
圆方树用来干啥?
——处理仙人掌的问题。
仙人掌是啥?

(图片来自于(BZOJ1023))
——也就是任意一条边只会出现在一个环里面。
当然,如果你的图片想看起来舒服一点,也可以把图片变成这样子
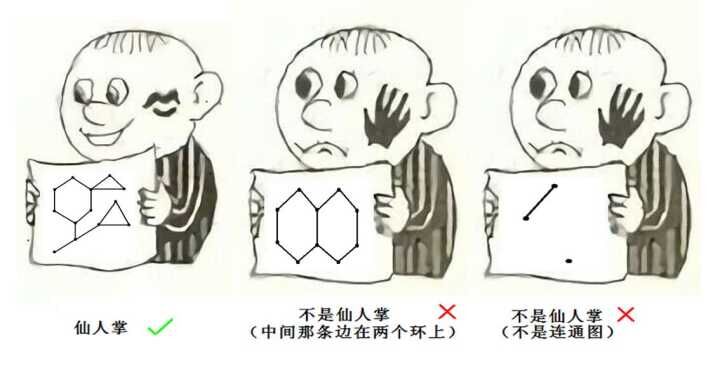
(图片来源于网络)
2、DFS树
为啥要写这个?--因为这个看起来也可以解决一些仙人掌的问题。
对于一个仙人掌,我们随便构建出一棵生成树。
然后我们就多了一些边——可以叫返祖边,非树边……你想叫啥就叫啥。
因为每条边只会出现在一个环中,
所以每一条返祖边覆盖了树中的一条链,这条链+这条边构成了环。
所以我们可以确定每条边都出现在了哪个环中。
这样子可以解决一点点仙人掌的问题。
比如仙人掌的最大独立集,(dp)的时候额外记录一下所在环的返祖边的端点的状态就好了。
3、圆方树是啥
看WC2017的营员交流的课件真的看得想死
先来定义一下什么是圆方树。
以下内容来自于课件:
仙人掌 (G = (V, E)) 的圆方树 (T = (V_T , E_T )) 为满足以下条件的无向图:
(V_ T = R_ T ∪ S_ T , R_ T = V, R_ T ∩ S_ T = ∅),我们称$ R_ T$ 集合为圆点、(S_ T)
集合为方点
(∀e ∈ E),若 (e) 不在任何简单环中,则 (e ∈ E_T)
对于每个仙人掌中的简单环 (R),存在方点 (p_ R ∈ S_ T) ,并且 (∀p ∈ R) 满
足 ((p _R , p) ∈ E_ T) ,即对每个环建方点连所有点
听说你看完挺混乱?
我来翻译一下:
对于一个仙人掌,它的圆方树如下定义:
首先分为了两类点,一类是圆点,一类是方点。
圆点就是原仙人掌中所有的点,方点是我们新添加进去的点。
而圆方树的连边规则是这样的:
如果一条边在仙人掌中不属于任何一个环中,那么它直接圆方树中的两个圆点。
对于仙人掌中的任意一个环,则每个环上的点在圆方树上对应的圆点向这个环对应的方点连边。
如何证明圆方树是一棵树?
(以下内容来自于课件)
不在环上的边在圆方树中依然存在,
因此这些边连通性不变;
每个环通过新建方点的方式连成一朵菊花,连通性不变。
因此圆方树是无向连通图。
原图中环的个数为 (|E| − |V| + 1),则
(|V _T | = |S _T | + |R_ T | = |V| + |E| − |V| + 1 = |E| + 1,|E _T | = |E|)(大小为(r) 的环在仙人掌和圆方树中都是 (r) 条边),因此满足 (|V_ T | = |E_ T | + 1)
证明分为了两步:
首先证明它是联通的。
然后就证明了点数=边数+1
这样就是一棵树了。
然后让我把课件上的一张图片给蒯过来
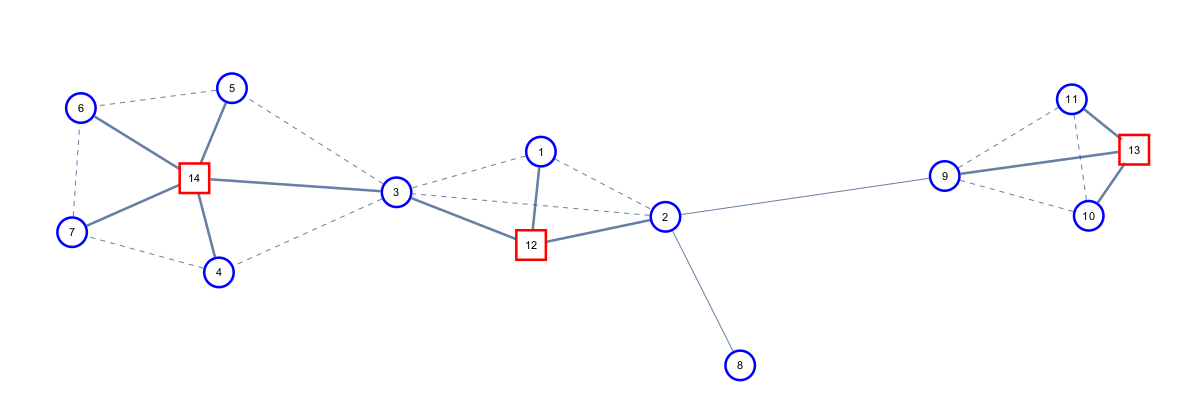
好的,圆方树就长成这个样子啦。
4、如何构建圆方树
我想,看了上面的东西,知道了圆方树是啥,我们很容易就知道怎么构建圆方树了吧。
首先(Tarjan)缩点,把每个大小超过(1)的环里面的所有点都向一个新点(方点)连边。
然后把多出来的链接两个圆点的边直接给连上就好了。
似乎真的很简单?
5、圆方树的性质
1.方点不会直接和方点相连
证明:
方点只会和属于一个强连通分量的点相连,显然不会和方点相连。
2.无论取哪个点为根,圆方树的形态是一样的
证明:
这不还是废话吗?
对于一个环,我们显然对应的是一个方点,无论以哪个点为根,
这个环是不会变的,除了方点的编号不一样之外就没有任何不同了。
所以圆方树是无根树。
定义:子仙人掌
以(r)为根的仙人掌上的点(p)的子仙人掌是去除掉(p)到(r)的所有简单路径后,(p)所在的联通块
3.以(r)为根的仙人掌上(p)的子仙人掌就是圆方树中以(r)为根时,(p)子树中的所有圆点
证明:
如果(p)不在环上,显然成立。
否则,此时去除所有到达根节点的所有简单路径后,
剩下的只有和(p)相连的,并且不和(p)在一个环内的点
显然是圆方树上(p)子树中的圆点(和它在一个环内的圆点都不和它直接相连了)
6、如何解决仙人掌上的一些简单的问题
a.求仙人掌的最大独立集(BZOJ4316)
这道题目显然有直接用(dfs)树的(dp)求法,见这里。
但是我们是在学习仙人掌,所以当然要用仙人掌的方法来求解啊。
其实这里圆方树没有必要出来,没有必要区分圆点和方点。
我们也是直接做(dp),但是与(dfs)树不同的是,
我们直接在(Tarjan)过程中做(dp)(似乎本质也是(dfs)树?)
碰到圆圆边(圆点和圆点直接的边)就是普通的树型(dp)进行转移
如果是一个环上的边的话,那么我们先暂时不进行操作。
当回到这个环的最上方的时候,对于这个环就行一次单独的(dp)
将答案累加给环的顶端,这样向上转移又和树一样了
b.求仙人掌直径(BZOJ1023)
和普通的树求直径用一样的(dp)就可以了。
对于一个环,拉出来特殊考虑,用一个单调队列维护一下。
具体的实现方法戳这里
c.仙人掌两点间的最短路(BZOJ2125)
构建出圆方树(圆方树:终于需要用到我了),直接把圆方树树链剖分(主要是用来求(LCA))
圆圆边和原仙人掌是同构的,圆方边的权值定义如下:
我们知道方点的父亲一定是圆点(转换为有根树之后),
这样子把每条圆方边的权值赋为到达方点父亲的最短路径就好啦。
更加详细的题解和代码戳这里。
这一部分的小节
前两个问题似乎用不到圆方树,只需要普通的(dp)即可解决。实现的方法和普通的树型(dp)是类似的,但是也有几点区别:首先不是普通的(dfs),而是(Tarjan)算法的实现过程中,顺带解决(dp)问题。另外一个是仙人掌上的问题需要额外处理环的问题,每次找到环之后需要特殊处理。所以,解决这类问题也就是两步:首先想好怎么在树上解决(圆圆边如何解决),然后想好怎么处理环的答案。
第三个问题就需要用到圆方树啦,然而本质仍然是处理环和普通的树边之间的关系,只需要把这层关系想清楚,这一类问题应该还是比较好解决的。
7、广义圆方树
前面的圆方树只能解决仙人掌的问题。
那么,对于一个一般的无向图,我们显然也是可以利用圆方树来解决的(要不然我写什么广义圆方树啊?)
我们在仙人掌中是对于每个点双构建一个方点,在一般图中我们也这么做。
然后方点向所有点双中的点连边,差不多和仙人掌上的圆方树是一样的啦。
当然,和仙人掌上的圆方树是有区别的啦,仙人掌上的圆方树是圆圆点之间是可能有边的。
那么,广义圆方树呢?
先蒯张图过来(来自(ppl)的(blog))
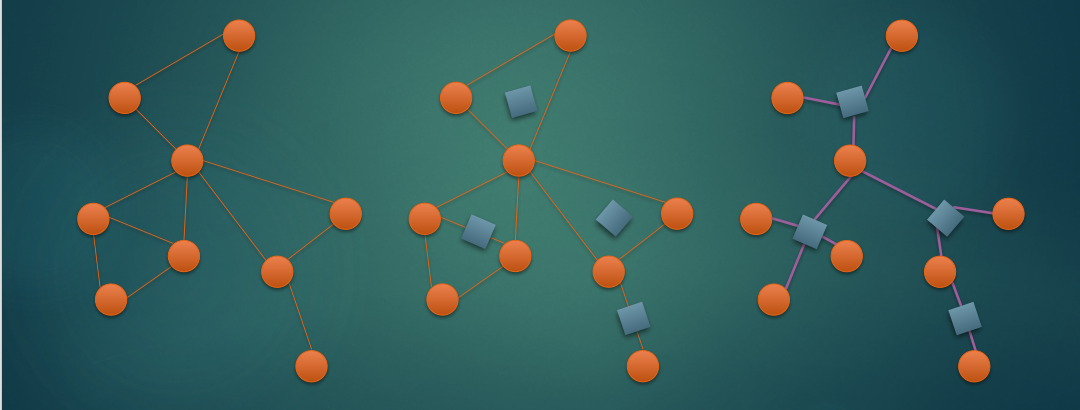
发现了啥?
圆点和方点是相间的,怎么搞?——强制把两个点也看成一个点双就好了
先找到题目来吧
带修改,求无向图中两点之间所有简单路径上的最小权值(CF487E)
首先我们不考虑修改,再来想想这道题目。
我们既然要求的是最小值,那么,在经过一个点双的时候,走的一定是具有较小权值的那一侧。
所以说,我们可以让所有的方点表示它所在的点双的最小权值,
这样子只需要对于圆方树树链剖分之后维护链的最小值就行了。
好的,回归带修改,无非是要动态的维护一下方点的最小权值了。
你问我怎么动态维护若干个值的最小值?搞个(multiset)不就好了吗?
但是,现在问题又来了,如果每次修改一个点的权值(这个点当然是圆点啦),
那么,必定会修改所有和它相邻的方点,如果是一个菊花树,然后我们拼命修改根节点,这样子复杂度就起飞了。
现在让我们打开脑洞,大力思考一下怎么办?
我们强行让方点的权值不包括它的父亲(也就是只算它的儿子)
如果求解的时候(LCA)是方点,则额外计算一下方点父亲的权值
这样子每个圆点在修改的之后只需要向上修改给父亲方点啦!
于是,我们得到了(Tarjan)+圆方树+树链剖分+线段树+(multiset)的(O(nlog^2n))的做法啦
(为什么要手写可删堆啊?(multiset)不好吗?)
8、完结撒花
呼,终于写完啦。
最后再来总的说一说仙人掌和圆方树。
对于仙人掌,我们对应的圆方树唯一。
无论是广义圆方树还是普通的圆方树,和普通的树相比,唯一的区别就是要额外考虑方点的贡献。
总的来说,就是码农+思维题啦,只要想清楚方点的处理,一切都很好办了。