势能分析
在数据结构问题中,我们往往难以估计第 (i) 次的实际时间开销 (t_i)。
所以我们要引入一些势能分析的概念:
- 设 (phi_i) 表示:第 (i) 次操作过后,数据结构的势能值。
- 记 (a_i = t_i + phi_i - phi_{i - 1}),即第 (i) 次操作的均摊时间。
注意:确定势能值的势函数是需要我们自己确定的,寻找一个优秀的势函数往往可以更容易解决问题。
假设执行了 (m) 次操作,那么总的实际时间为:
[sumlimits_{1 leq i leq m} t_i = sumlimits_{1 leq i leq m} a_i + phi_0 - phi_m
]
所以知道了 (a_i, phi) 的复杂度就可以求出总的实际时间了。
splay 的复杂度分析
在 splay 中,我们取这样的一个势函数:
- 设当前状态下,节点 (x) 的势能值 (F(x) = log ext{size}_x)。
- 设当前状态下,整棵 splay 的势能值 (phi = sumlimits_{1 leq i leq n} F(i))。
接下来要证明的结论是:
[egin{aligned}a_i & leq 3(F(x') - F(x)) + 1 \& = mathcal{O}left(log frac{n}{ ext{size}_x}
ight) = mathcal{O}(log n)end{aligned}
]
其中 (F(x), F(x')) 分别表示伸展 (x) 前和伸展 (x) 后节点 (x) 的势能值。
双旋 splay 的三种旋转
来回顾一下双旋 splay 的三种旋转:
-
当 (x) 的父亲 (p) 是根节点时,直接 zig/zag (x)。
-
当 (x) 和上两代祖先位于一条链上:先 zig/zag (p),再 zig/zag (x)。
-
当 (x) 和上两代祖先是分叉时:先 zig/zag (x),再 zig/zag (x)。
第一种旋转的均摊分析(以 zig 为例)
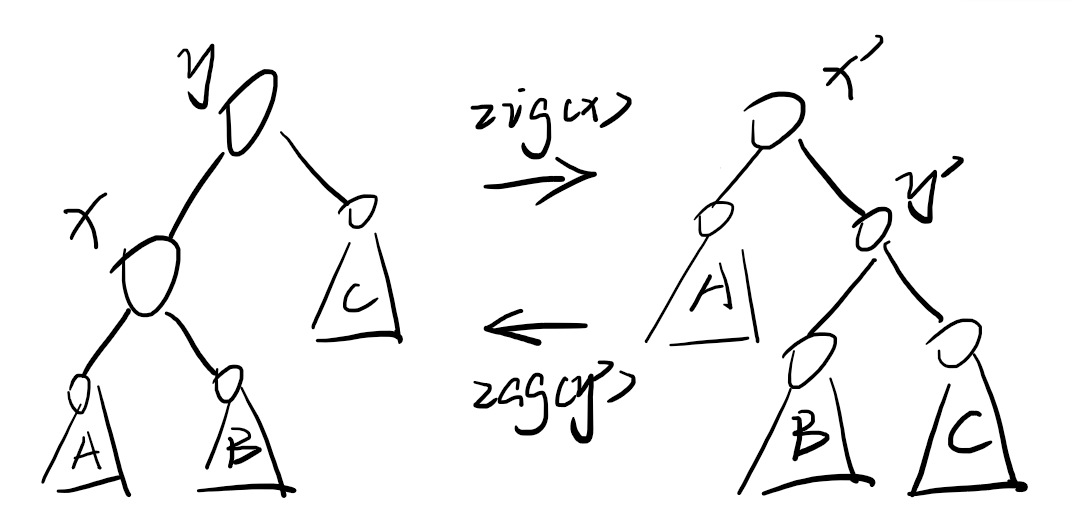
简单分析一下:
-
时间开销:旋转了一次。
-
势能变化:子树大小只有节点 (x, y) 发生了变化,故只有节点 (x, y) 的势能值发生了变化。
所以可以得到:
[egin{aligned}a_{ ext{zig}} & = 1 + F(x') + F(y') - F(x) - F(y) \& = 1 + F(y') - F(x)end{aligned}
]
适当放缩得:
[a_{ ext{zig}} leq 3(F(x') - F(x)) + 1
]
第二种旋转的均摊分析(以 zig-zig 为例)
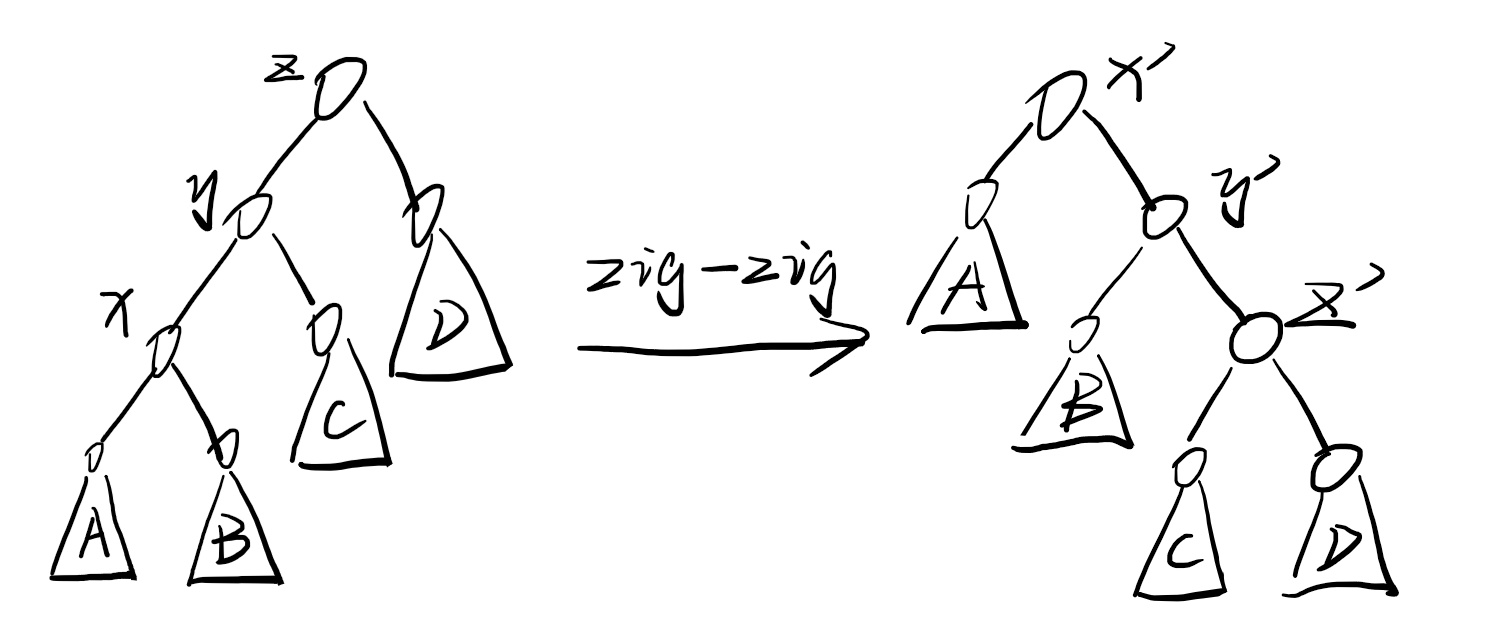
简单分析一下:
- 时间开销:旋转了两次。
- 势能变化:子树大小只有节点 (x, y, z) 发生了变化,故只有节点 (x, y, z) 的势能值发生了变化。
所以可以得到:
[egin{aligned}a_{ ext{zig-zig}} & = 2 + F(x') + F(y') + F(z') - F(x) - F(y) - F(z) \& = 2 + F(y') + F(z') - F(x) - F(y)end{aligned}
]
然后你发现这个多出来的 (2) 非常令人不爽。
注意到:
[F(x) + F(z') - 2 cdot F(x') leq log frac{ ext{size}_x cdot ext{size}_{z'}}{ ext{size}^2_{x'}} leq -2
]
(将上式对数的底数看成 (2),用均值不等式即可证明,大家都会。)
然后将这两个式子合并可以得到:
[a_{ ext{zig-zig}} leq 2 cdot F(x') + F(y') - 2 cdot F(x) - F(y)
]
适当放缩得:
[a_{ ext{zig-zig}} leq 3(F(x') - F(x))
]
第三种旋转的均摊分析(以 zig-zag 为例)
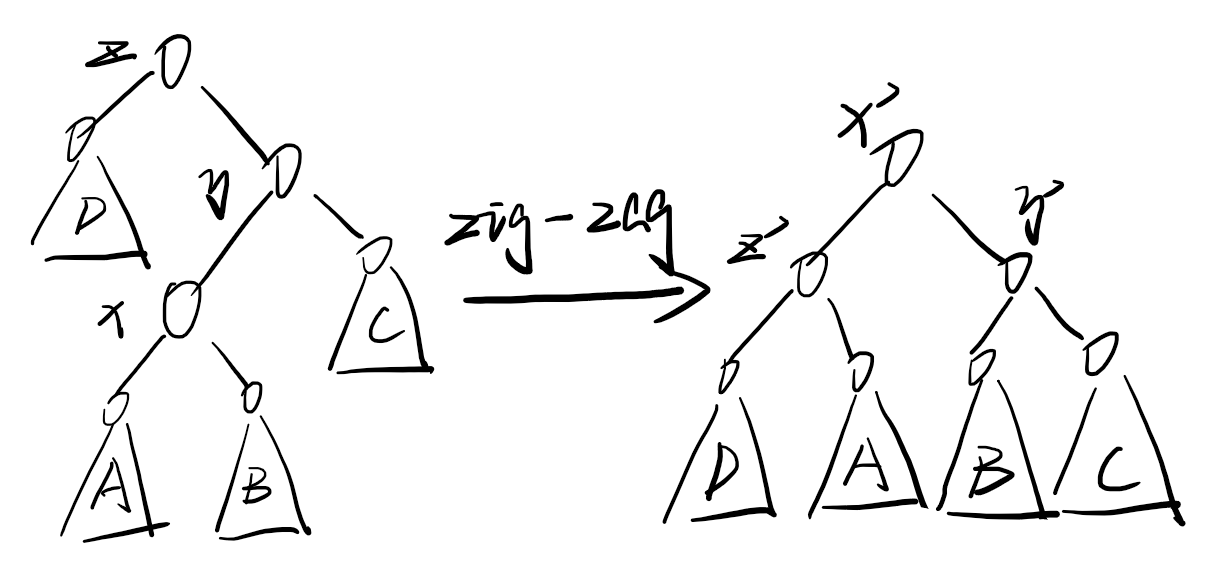
简单分析一下:
- 时间开销:旋转了两次。
- 势能变化:子树大小只有节点 (x, y, z) 发生了变化,故只有节点 (x, y, z) 的势能值发生了变化。
所以可以得到:
[egin{aligned}a_{ ext{zig-zag}} & = 2 + F(x') + F(y') + F(z') - F(x) - F(y) - F(z) \& = 2 + F(y') + F(z') - F(x) - F(y)end{aligned}
]
注意到:
[F(x) + F(z') - 2 cdot F(x') leq log frac{ ext{size}_x cdot ext{size}_{z'}}{ ext{size}^2_{x'}} leq -2
]
然后将这两个式子合并可以得到:
[a_{ ext{zig-zag}} leq 2 cdot F(x') + F(y') - 2 cdot F(x) - F(y)
]
适当放缩得:
[a_{ ext{zig-zag}} leq 3(F(x') - F(x))
]
根据上述证明,我们可以知道,在一次操作中,伸展一个节点 (x) 的时候,将每次旋转的贡献式子连接起来,消除相邻的项,然后就可以得到:
[egin{aligned}a_i & leq 3(F(x') - F(x)) + 1 \& = mathcal{O}left(log frac{n}{ ext{size}_x}
ight) = mathcal{O}(log n)end{aligned}
]
然后你会发现:
- 因为 (a_i = mathcal{O}(log n)),所以 (sumlimits_{1 leq i leq m} a_i = mathcal{O}(m log n))。
- 因为 (0 leq phi leq n log n),所以 (phi_0 - phi_m = mathcal{O}(n log n))。
于是 splay 的时间复杂度即为 (mathcal{O}((n + m) log n))。