Preface
由于我怕学习了Splay之后不直接写blog第二天就忘了,所以强行加了一波优先级。
论谁是天下最秀平衡树,我Splay第一个不服。维护平衡只靠旋转。
一言不合转死你
由于平衡树我也介绍了两种Treap&&Scapegoat Tree,所以一些互通的东西也不讲了。
这次的亮点主要是为了弥补Splay的巨大常数(据说是96),我把大量的函数都写成了迭代版本。
废话不多说开讲。
维护平衡的方式——旋转
关于旋转操作,在Treap的那篇文章中已经讲的比较详细了。
但是注意一下Splay的旋转不同于Treap,一般Splay旋转时简单的理解就是儿子翻身当爸爸
什么意思,其实像这样:
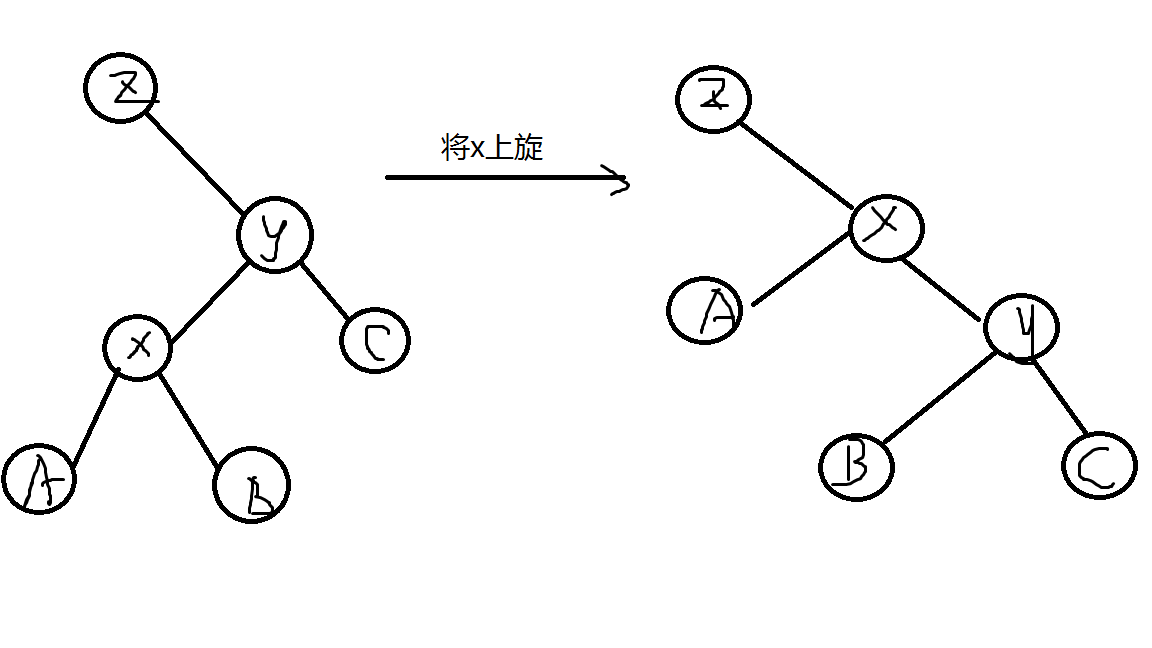
(x,y)的关系还是很好理解的,主要是(x)的某个儿子被旋到哪里去了旋的头晕
我们再手玩几种情况:
-
(y)是(z)的左儿子 (x)是(y)的左儿子
-
(y)是(z)的左儿子 (x)是(y)的右儿子
-
(y)是(z)的右儿子 (x)是(y)的右儿子
疯狂手玩ing
那我们来总结一波性质吧:
- 我们把(x)转到了原来(y)的位置(这个很简单,因为我们旋转的本意就是让(x)儿子变爸爸)
- (x)是(y)的哪个儿子,那么旋转完之后,(x)的那个儿子就不会变(多玩几次就好了,证明也比较简单)
- 如果原来(x)是(y)的哪一个儿子,那么旋转完之后(y)就是(x)的另外一个儿子
然后我们就可以搞出旋转的核心代码了(具体看下面)
一波操作上天——伸展
为什么Splay要叫Splay呢。请自行使用词典查询Splay的意思。好了我懂了
一个节点已经不满足屈膝于它人的儿子了,我就是想俯视众生
正常的说,就是想要当根节点。真有梦想
那么让你飞,但是我只需要无脑暴力上旋就可以维护平衡这一重要性质了吗?
我将一个(x)进行上旋操作,像这样:

不是说好了要当根的吗,那我把(x)再旋转一波:

然后我们很意外的发现,红色的那一条链一点都没有改变
也就意味这数据还是可以把你给卡掉
然后我们发现,对于(x,y,z)的不同位置情况,我们要分别进行讨论
然后蒟蒻就开始(2^3=8)种情况大力讨论
手玩了好久好久。。。。。。
其实简化了之后也就两种:
- (x)和(y)分别是(y)和(z)的同一个儿子
- (x)和(y)分别是(y)和(z)的不同儿子
而对于情况一,也就是类似上面给出的图的情况,就要考虑先旋转(y)再旋转(x)
而对于情况二,自己画一下图,发现就是对(x)旋转两次,先旋转到(y)再旋转到(x)
于是我们就可以简化一波操作,就完成了Splay的核心内容。
其它操作及模板
其它的一些操作都是具有BST性质的了,就是主要一点:
有事没事Splay一下要不然干嘛叫Splay
还是板子题:Luogu P3369 【模板】普通平衡树的CODE(跑的并不慢)
#include<cstdio>
#include<cctype>
#define lc(x) (node[x].ch[0])
#define rc(x) (node[x].ch[1])
#define fa(x) (node[x].fa)
#define tc() (A==B&&(B=(A=fl)+fread(fl,1,S,stdin),A==B)?EOF:*A++)
#define pc(ch) (top<S?st[top++]=ch:(fwrite(st,1,S,stdout),st[(top=0)++]=ch))
using namespace std;
const int N=100005,S=1<<20,INF=2147483647;
char fl[S],st[S],*A=fl,*B=fl;
struct Splay
{
int ch[2],size,cnt,fa,val;
}node[N];//同Treap,注意记录节点重复个数
int n,opt,x,rt,tot,top;
inline void read(int &x)
{
x=0; char ch; int flag=1; while (!isdigit(ch=tc())) flag=ch^'-'?1:-1;
while (x=(x<<3)+(x<<1)+ch-'0',isdigit(ch=tc())); x*=flag;
}
inline void write(int x)
{
if (x<0) pc('-'),x=-x;
if (x>9) write(x/10); pc(x%10+'0');
}
inline void pushup(int now)//更新操作,和一般的BST大同小异
{
node[now].size=node[lc(now)].size+node[rc(now)].size+node[now].cnt;
}
inline int build(int val,int fa)//新建一个节点
{
node[++tot].val=val; node[tot].size=node[tot].cnt=1; fa(tot)=fa;
lc(tot)=rc(tot)=0; if (fa) node[fa].ch[val>node[fa].val]=tot; return tot;
}
inline int identify(int now)//确认一个点是它父亲的左儿子(0)还是右儿子(1)
{
return node[fa(now)].ch[1]==now;
}
inline void connect(int son,int fa,int d)//链接两个节点,d(0/1)表示方向
{
fa(son)=fa; node[fa].ch[d]=son;
}
inline void rotate(int now)//核心操作,上旋。注意connect的次序,最容易写错的就是pushup,不能pushup反了
{
int x=node[now].fa,y=node[x].fa,dx=identify(now),dy=identify(x),son=node[now].ch[dx^1];
connect(son,x,dx); connect(x,now,dx^1); connect(now,y,dy); pushup(x); pushup(now);
}
inline void splay(int now,int tar)//splay,将now伸展成为tar的儿子,注意讨论父节点即为根的情况
{
while (fa(now)!=tar)
{
if (fa(fa(now))!=tar)
{
if (identify(now)^identify(fa(now))) rotate(now); else rotate(fa(now));
} rotate(now);
}
if (!tar) rt=now;
}
inline void get_rank(int val)//查询一个点的排名,并把它旋转到根
{
int now=rt; if (!now) return;
while (node[now].val!=val&&node[now].ch[val>node[now].val])
now=node[now].ch[val>node[now].val]; splay(now,0);
}
inline int get_val(int rk)//得到排名为rk的值
{
int now=rt;
for (;;)
{
if (rk>node[lc(now)].size+node[now].cnt) rk-=node[lc(now)].size+node[now].cnt,now=rc(now);
else if (node[lc(now)].size>=rk) now=lc(now); else return node[now].val;
}
}
inline int next(int val,int d)//精简的求前驱(0),后继(1)的过程,注意特判
{
get_rank(val); int now=rt;
if ((node[now].val>val&&d)||(node[now].val<val&&!d)) return now;
now=node[now].ch[d]; while (node[now].ch[d^1]) now=node[now].ch[d^1]; return now;
}
inline void insert(int val)//插入一个新的节点,由于此时平衡性得不到保证所以又要splay到根
{
int now=rt,fa=0;
while (now&&node[now].val!=val) fa=now,now=node[now].ch[val>node[now].val];
if (!now) now=build(val,fa); else ++node[now].cnt; splay(now,0);
}
inline void remove(int val)//删除就是把一个点的前驱后继都旋上去,此时这个点就成为叶子节点了,再进行删除
{
int lst=next(val,0),nxt=next(val,1); splay(lst,0); splay(nxt,lst); int del=lc(nxt);
if (node[del].cnt>1) --node[del].cnt,splay(del,0); else lc(nxt)=0;
}
int main()
{
//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
register int i; read(n); insert(-INF); insert(+INF);
for (i=1;i<=n;++i)
{
read(opt); read(x);
switch (opt)
{
case 1:insert(x);break;
case 2:remove(x);break;
case 3:get_rank(x),write(node[lc(rt)].size),pc('
');break;
case 4:write(get_val(x+1)),pc('
');break;
case 5:write(node[next(x,0)].val),pc('
');break;
case 6:write(node[next(x,1)].val),pc('
');break;
}
}
return fwrite(st,1,top,stdout),0;
}
平衡树的精髓在于它们不同的维护平衡的方式:
- Treap的代码精简且常数较小,是解决大部分平衡树问题的最好工具
- Scapegoat Tree的思想易于理解,且一般情况下速率良好。其内核的思想也应用到了许多其他的地方
- Splay由于它特殊的旋转性质,使其可以像线段树一样维护区间,也是LCT的辅助树,功能强大。
常数也很大