Preface
没啥好说的干就完了
A - Poisonous Cookies
SB题
#include<cstdio>
#include<iostream>
#define RI register int
#define CI const int&
using namespace std;
int a,b,c;
int main()
{
return scanf("%d%d%d",&a,&b,&c),printf("%d",b+min(a+b+1,c)),0;
}
B - Tree Burning
考虑显然存在一个转折点,满足从起点直接走到这个点之后再反复横跳使得答案最优
大力枚举转折点,用前缀和优化一下就是(O(n))的了
注意细节
#include<cstdio>
#include<iostream>
#define RI register int
#define CI const int&
using namespace std;
const int N=200005;
int l,n,a[N]; long long pfx[N],sfx[N],ans;
int main()
{
RI i; for (scanf("%d%d",&l,&n),i=1;i<=n;++i) scanf("%d",&a[i]);
for (i=1;i<=n;++i) pfx[i]=pfx[i-1]+a[i]; for (i=n;i;--i) sfx[i]=sfx[i+1]+l-a[i];
for (i=1;i<n;++i)
ans=max(ans,2LL*a[i]+2LL*(pfx[i+n>>1]-pfx[i])+2LL*sfx[(i+n>>1)+1]-((n-i)&1?l-a[(i+n>>1)+1]:a[i+n>>1]));
for (i=n;i>1;--i)
ans=max(ans,2LL*(l-a[i])+2LL*(sfx[i+2>>1]-sfx[i])+2LL*pfx[(i+2>>1)-1]-((i-1)&1?a[(i+2>>1)-1]:l-a[i+2>>1]));
return printf("%lld",max(ans,(long long)max(a[n],l-a[1]))),0;
}
C - Coloring Torus
《论我如何在看错题目的情况下和陈指导交谈甚欢》
首先我们不难有一个想法,假设矩阵的行列从(0)到(n-1)标号,那么我们把((i,j))染成((i+j)operatorname{mod} n+1)显然一定合法
但是此时需要大小为(k)的矩阵,而(n)的范围只有(500),这提示我们需要减半矩阵大小
换句话说要在矩形大小不变的情况下翻倍颜色数量
观察到按照上面的染色方法每次同种颜色的是两条副对角线(或是一条主对角线),因此我们发现可以给对应对角线上的一种颜色交错地染上两种颜色
稍微分析一下就会发现当(n)为偶数的时候一定是正确的,并且可以根据(k)的奇偶性进行调整,因此可以通过本题
#include<cstdio>
#define RI register int
#define CI const int&
using namespace std;
const int N=505;
int n,k,a[N][N];
int main()
{
RI i,j,t; scanf("%d",&k); n=(k+3)/4*2;
if (k==1) return puts("1
1"),0;
for (i=0;i<n;++i) for (j=0;j<n;++j) a[i][j]=(i+j)%n;
for (t=n;t<k;++t) for (i=0;i<n;++i) for (j=0;j<n;++j)
if (t%n==a[i][j]) a[i][j]+=(i&1)*n; printf("%d
",n);
for (i=0;i<n;++i) for (j=0;j<n;++j) printf("%d%c",a[i][j]+1,"
"[j==n-1]);
return 0;
}
D - Inversion Sum
炒鸡妙的一题,被DD了
我们先来考虑一个暴力的想法,枚举一个数对(x,y),若(a_x>a_y)那么我们考虑统计进行(Q)次操作后(a_x)在(a_y)之前的方案数
可以设计一个DP,(f_{t,i,j})表示进行了前(t)次操作,(a_x)在位置(i)且(a_y)在位置(j)的方案数,显然有初始值(f_{0,x,y}=1),转移也很容易(设第(t)次操作可以操作的位置为(x,y)):
容易发现每次枚举到一个操作时,只会有(O(n))级别的数组被更新,因此我们可以借鉴一个经典套路,每次转移的时候除以(2),这样第一种转移就无需考虑了,只需要在最后乘上(2^Q)即可
然后我们仔细一想,每一个数对(a_x,a_y)的转移过程其实都是一样的,换句话说我们只要给多个(f_{0,x,y})都赋好初值那么就可以全部一起转移
最后统计所有的(i<j)的状态(f_{t,i,j})即可,复杂度为(O(n^2))
#include<cstdio>
#define RI register int
#define CI const int&
using namespace std;
const int N=3005,mod=1e9+7;
int n,q,f[N][N],inv2,mul,a[N],tx[N],ty[N],ans;
inline int quick_pow(int x,int p=mod-2,int mul=1)
{
for (;p;p>>=1,x=1LL*x*x%mod) if (p&1) mul=1LL*mul*x%mod; return mul;
}
inline int sum(CI x,CI y)
{
int t=x+y; return t>=mod?t-mod:t;
}
int main()
{
RI i,j; for (scanf("%d%d",&n,&q),i=1;i<=n;++i) scanf("%d",&a[i]);
for (i=1;i<=q;++i) scanf("%d%d",&tx[i],&ty[i]); inv2=quick_pow(2);
for (i=1;i<=n;++i) for (j=1;j<=n;++j) if (i!=j&&a[i]>a[j]) ++f[i][j];
for (mul=quick_pow(2,q),i=1;i<=q;++i)
{
int x=tx[i],y=ty[i]; f[x][y]=f[y][x]=1LL*sum(f[x][y],f[y][x])*inv2%mod;
for (j=1;j<=n;++j) if (j!=x&&j!=y) f[x][j]=f[y][j]=1LL*sum(f[x][j],f[y][j])*inv2%mod;
for (j=1;j<=n;++j) if (j!=x&&j!=y) f[j][x]=f[j][y]=1LL*sum(f[j][x],f[j][y])*inv2%mod;
}
for (i=1;i<=n;++i) for (j=1;j<=n;++j) if (i<j) ans=sum(ans,1LL*f[i][j]*mul%mod);
return printf("%d",ans),0;
}
E - Less than 3
妙如舟来了都没它妙的题。以下图片出自官方题解
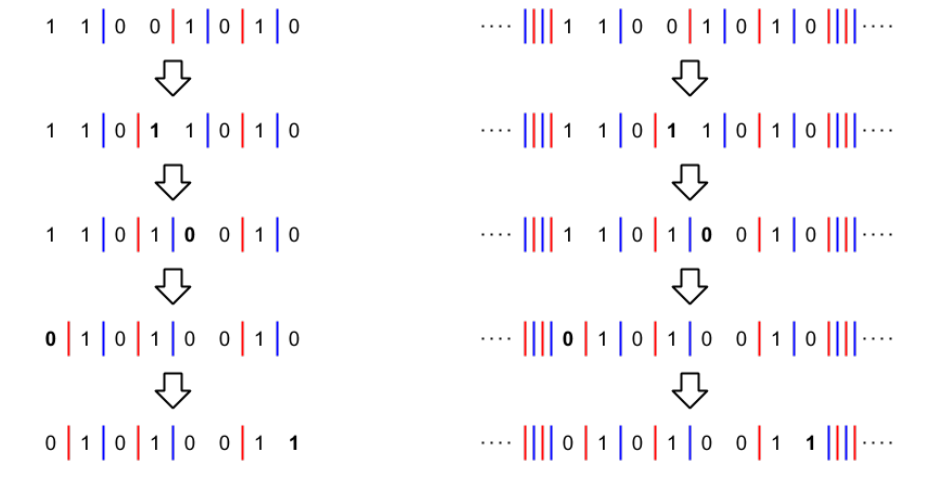
我们考虑在序列的相邻的(01)之间连一条红线,在相邻的(10)之间连一条蓝线
考虑到我们需要一直满足三个相连的数不同的性质,其实也就是告诉我们每次修改的时候线只会导致线向相邻的位置移动
同时显然红蓝线一定是交替出现的,但是当修改在边界上时可能会导致多出一条线
因此我们先在左右两边将红蓝线无限延伸下去,那么我们的目的就是让(s,t)的红蓝线一一对应
观察一下可以发现一组对应的边需要修改花费的代价恰好是他们之间的距离
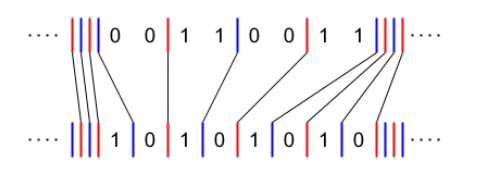
我们可以大力枚举(s)中于(t)的开头匹配的位置,暴力算答案取最小值即可
注意特判中间没线的情况,复杂度(O(n^2))
#include<cstdio>
#include<algorithm>
#define RI register int
#define CI const int&
using namespace std;
const int N=5005;
int n,sa[N<<2],sb[N<<2],ans; char s[N],t[N];
inline void calc(int ret=1e9)
{
RI i,j,ta=0,tb=0; for (i=1;i<=n;++i) sa[++ta]=0;
for (i=1;i<n;++i) if (s[i]=='1'&&s[i+1]=='0') sa[++ta]=i;
for (i=1;i<=n;++i) sa[++ta]=n;
for (i=1;i<n;++i) if (t[i]=='1'&&t[i+1]=='0') sb[++tb]=i;
for (i=1;i+n-1<=ta;++i)
{
int cur=0; for (j=1;j<i;++j) cur+=sa[j];
for (j=1;j<=tb;++j) cur+=abs(sa[i+j-1]-sb[j]);
for (j=i+tb;j<=ta;++j) cur+=n-sa[j]; ret=min(ret,cur);
}
ans+=ret;
}
int main()
{
RI i; scanf("%d%s%s",&n,s+1,t+1);
if (n==1) return puts(s[1]==t[1]?"0":"1"),0;
if (n==2&&s[1]!=t[1]&&s[1]==s[2]&&t[1]==t[2]) return puts("2"),0;
for (calc(),i=1;i<=n;++i) s[i]=48+((s[i]-48)^1),t[i]=48+((t[i]-48)^1);
return calc(),printf("%d",ans),0;
}
F - Permutation and Minimum
ORZ使用神仙算法秒了这题的陈指导
首先我们发现没一对数有三种情况,显然当两个位置都有数的情况无需考虑
然后我们发现对于所有两个位置都没数的数对(设有(cnt)对),我们可以假定它们本质相同然后最后乘上(cnt!)即可(这样可以使得转移无需乘上系数),我们把这样的数对称为不在序列中
接下来就比较容易了,我们设(f_{i,j,k})表示做了(ge i)的数,其中在序列中未被匹配的数有(j)个,不在序列中的未被匹配的数有(k)个,转移时只有与序列中的数匹配才会乘上系数
复杂度(O(n^3))
#include<cstdio>
#define RI register int
#define CI const int&
using namespace std;
const int N=605,mod=1e9+7;
int n,m,a[N<<1],f[N<<1][N][N],cur,q[N<<1],tp; bool ext[N<<1],vis[N<<1];
inline void inc(int& x,CI y)
{
if ((x+=y)>=mod) x-=mod;
}
int main()
{
RI i,j,k; for (scanf("%d",&n),i=1;i<=2*n;++i)
scanf("%d",&a[i]),ext[~a[i]?a[i]:0]=1;
for (i=1;i<=n;++i) if (!~a[2*i-1]&&!~a[2*i]) ++cur;
else if (~a[2*i-1]&&~a[2*i]) vis[a[2*i-1]]=vis[a[2*i]]=1;
for (i=1;i<=2*n;++i) if (!vis[i]) q[++m]=ext[i];
for (n=m,f[n][0][0]=1,i=n;i;--i) for (j=0;j<=n;++j)
for (k=0;k<=n;++k) if (tp=f[i][j][k])
{
if (q[i]) inc(f[i-1][j+1][k],tp),k&&(inc(f[i-1][j][k-1],tp),0);
else inc(f[i-1][j][k+1],tp),k&&(inc(f[i-1][j][k-1],tp),0),j&&(inc(f[i-1][j-1][k],1LL*tp*j%mod),0);
}
int ans=f[0][0][0]; for (i=1;i<=cur;++i) ans=1LL*ans*i%mod;
return printf("%d",ans),0;
}
Postscript
STO CXR ORZ