Preface
这场CC好难的说,后面的都不会做QAQ
还因为不会三进制位运算卷积被曲明姐姐欺负了,我真是太菜了QAQ
PS:最后还是狗上了六星的说,期待两(三)场之内可以上七星
Physical Exercise
本来T1放的是一个思维题,然后被Ban了现在变成一个SB题了
爆枚前两个点集的点,然后预处理前两个点集的每个点与第三个点集所有点之间距离的最小值即可通过此题
#include<cstdio>
#include<cmath>
#include<iostream>
#define RI register int
#define CI const int&
using namespace std;
const int N=5005; double INF=1e18;
int t,n,m,k,x,y,a[N],b[N],c[N],d[N],e[N],f[N]; double ans,g[N<<1];
inline double dis(CI a,CI b,CI c,CI d)
{
return sqrt(1LL*(a-c)*(a-c)+1LL*(b-d)*(b-d));
}
int main()
{
for (scanf("%d",&t);t;--t)
{
RI i,j; scanf("%d%d%d%d%d",&x,&y,&n,&m,&k);
for (i=1;i<=n;++i) scanf("%d%d",&a[i],&b[i]);
for (i=1;i<=m;++i) scanf("%d%d",&c[i],&d[i]);
for (i=1;i<=k;++i) scanf("%d%d",&e[i],&f[i]);
for (i=1;i<=n;++i) for (g[i]=INF,j=1;j<=k;++j)
g[i]=min(g[i],dis(a[i],b[i],e[j],f[j]));
for (i=1;i<=m;++i) for (g[n+i]=INF,j=1;j<=k;++j)
g[n+i]=min(g[n+i],dis(c[i],d[i],e[j],f[j]));
for (ans=INF,i=1;i<=n;++i) for (j=1;j<=m;++j)
ans=min(ans,dis(x,y,a[i],b[i])+dis(a[i],b[i],c[j],d[j])+g[n+j]),
ans=min(ans,dis(x,y,c[j],d[j])+dis(c[j],d[j],a[i],b[i])+g[i]);
printf("%.10lf
",ans);
}
return 0;
}
Smallest Beautiful Number
刚开始写了个很ZZ的爆搜,后来改了一下搜的方法就过了233
分析题意我们发现前面填上一大串(1)然后再考虑后面显然是最优的
那么我们直接爆搜每个数字的数目,最后显然是按序输出字典序最小
由于答案的(1)的数目很小因此可以通过此题
#include<cstdio>
#include<cmath>
#define RI register int
#define CI const int&
using namespace std;
const int sqr[10]={0,1,4,9,16,25,36,49,64,81};
int t,n,num[10]; bool flag;
inline bool is_sqr(CI x)
{
int tp=sqrt(x); return tp*tp==x;
}
inline void DFS(CI nw=1,CI lst=n,CI sum=0)
{
if (flag) return; if (nw>9) { if (!lst&&is_sqr(sum)) flag=1; return; }
for (RI i=lst;~i;--i)
{
num[nw]=i; DFS(nw+1,lst-i,sum+sqr[nw]*i);
if (flag) return;
}
}
int main()
{
for (scanf("%d",&t);t;--t)
{
RI i,j; scanf("%d",&n); flag=0; DFS();
for (i=1;i<=9;++i) for (j=1;j<=num[i];++j) putchar(i+'0');
for (putchar('
'),i=1;i<=9;++i) num[i]=0;
}
return 0;
}
From Zero to Infinity
考虑怎么区分两个串,经过一波推导我们发现显然如果连续的三个数都不满足就一定可以区分开来
然后考虑怎么计算答案,直接乘除显然要炸,但由于这里只涉及乘除,因此我们取个(ln)最后(exp)回去即可
然后这么写在(lle 10)的时候会损失一定的精度,因此我们暴力特判一下即可
#include<cstdio>
#include<cstring>
#include<cmath>
#include<iostream>
#define RI register int
#define CI const int&
#define Ms(f,x) memset(f,x,sizeof(f))
using namespace std;
const int N=100005,S=1e7+5,R=30;
int t,l,n,m,len,ax[R],ay[R],bx[R],by[R];
bool vis[R]; char s[S]; double ans;
inline bool is_vowel(const char& ch)
{
return ch=='a'||ch=='e'||ch=='i'||ch=='o'||ch=='u';
}
inline void calc(int *x,int *y)
{
Ms(vis,0); for (RI i=1;i<=len;++i)
++y[s[i]-'a'],!vis[s[i]-'a']&&(++x[s[i]-'a'],vis[s[i]-'a']=1);
}
int main()
{
//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
for (scanf("%d",&t);t;--t)
{
RI i,j; for (scanf("%d",&l),i=1;i<=l;++i)
{
scanf("%s",s+1); len=strlen(s+1); s[len+1]='a'; bool flag=1;
for (j=1;j+2<=len+1;++j) if (is_vowel(s[j])+is_vowel(s[j+1])+is_vowel(s[j+2])<=1)
{ flag=0; break; } if (flag) ++n,calc(ax,ay); else ++m,calc(bx,by);
}
if (l<=10)
{
for (ans=1,i=0;i<26;++i)
{
if (ax[i]) ans*=(1.0*ax[i]/pow(ay[i],n));
if (bx[i]) ans*=(1.0*pow(by[i],m)/bx[i]);
}
if (ans>1e7) puts("Infinity"); else printf("%.10lf
",ans);
} else
{
for (ans=0,i=0;i<26;++i)
{
if (ax[i]) ans+=log(ax[i])-1.0*n*log(ay[i]);
if (bx[i]) ans+=1.0*m*log(by[i])-log(bx[i]);
}
if (ans>log(1e7)) puts("Infinity"); else printf("%.10lf
",exp(ans));
}
n=m=0; Ms(ax,0); Ms(ay,0); Ms(bx,0); Ms(by,0);
}
return 0;
}
Single Point of Failure
刚开始想了个假算法233,一个点在每个环上再删去这个点不一定使得图中无环
后来想到了判无环图的套路后就很容易了,由于无环图一定满足点数-边数=联通块数
我们考虑删去每个点后的图的这三个东西怎么计算,前两个显然很容易求,那么后面那个怎么办
其实也很简单,我们考虑对这张图做一个类似于求割点的Tarjan,然后在DFS的时候:
- 当前点为根节点,那么我们统计它向子树内连的边数目(c),那么删去它会使得联通块数目增加(c-1)
- 当前的不是根节点,我们统计它向子树内连的点,满足这个点无法通过返祖边走到这个点前面的点个数(c),那么删去它会使得联通块数目增加(c)
然后注意清空下数组就做完了
#include<cstdio>
#include<iostream>
#include<cstring>
#define RI register int
#define CI const int&
#define Ms(f,x) memset(f,x,sizeof(f))
using namespace std;
const int N=100005;
struct edge
{
int to,nxt;
}e[N<<1]; int t,n,m,x,y,head[N],cnt,num,tot,deg[N],dfn[N],low[N],c[N];
inline void addedge(CI x,CI y)
{
e[++cnt]=(edge){y,head[x]}; head[x]=cnt; ++deg[x];
e[++cnt]=(edge){x,head[y]}; head[y]=cnt; ++deg[y];
}
#define to e[i].to
inline void Tarjan(CI now,CI fa=0)
{
dfn[now]=low[now]=++tot; int ret=0;
for (RI i=head[now];i;i=e[i].nxt)
if (!dfn[to])
{
Tarjan(to,now); low[now]=min(low[now],low[to]);
if (fa&&low[to]>=dfn[now]) ++c[now]; ++ret;
} else if (to!=fa) low[now]=min(low[now],dfn[to]);
if (!fa) c[now]=ret-1;
}
#undef to
inline void clear(void)
{
Ms(head,0); Ms(dfn,0); Ms(deg,0); Ms(c,0); cnt=num=tot=0;
}
int main()
{
//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
for (scanf("%d",&t);t;--t)
{
RI i; for (scanf("%d%d",&n,&m),i=1;i<=m;++i)
scanf("%d%d",&x,&y),addedge(x,y); int cur=0;
for (i=1;i<=n;++i) if (!dfn[i]) Tarjan(i),++num;
if (n-m==num) { puts("-1"); clear(); continue; }
for (i=1;i<=n;++i) if (n-1-(m-deg[i])==(num+c[i])) { cur=i; break; }
if (cur) printf("%d
",cur); else puts("-1"); clear();
}
return 0;
}
Winning Ways
转化三步曲。首先我们观察博弈的部分,发现拿每堆石子的时候只能拿成它约数的情况
那么我们统计出每个数的约数个数(d),那么每堆石子就变成了一个数目为(d-1)的Nim游戏
显然直接计算这部分的复杂度是(O(npi(sqrt{10^9})))的
然后接下来我们发现这个游戏和传统的Nim不太一样,她可以一次取(1/2)堆
其实这个问题就是个Nim-K问题,结论就是:
把(n)堆石子的石子数用二进制表示,统计每个二进制位上(1)的个数,若每一位上(1)的个数(mod (k+1))全部为(0),则必败,否则必胜。
证明可以看下某大佬写的Nim 游戏及其变形,这里不再赘述
然后我们发现此时我们只要统计出(k)次操作后(0)的个数即可。然后稍加分析发现合并两个状态时我们做的是三进制不进位加法
接下来就很容易了,我们搞出它的转移系数之后直接求(k)次幂就可以了,具体的DFT和IDFT过程参考:UOJ #272. 【清华集训2016】石家庄的工人阶级队伍比较坚强
综上这题就做完了,注意一个细节:求出约数个数后一定要转成三进制!!!
#include<cstdio>
#include<cstring>
#define RI register int
#define CI const int&
using namespace std;
const int mod=1e9+7;
const int N=100005,S=32000,lim=177147;
int t,n,k,x,prime[S+5],cnt; bool vis[S+5];
inline int sum(CI x,CI y)
{
int t=x+y; return t>=mod?t-mod:t;
}
inline int sub(CI x,CI y)
{
int t=x-y; return t<0?t+mod:t;
}
struct Complex
{
int x,y; //x+y*w
inline Complex(CI X=0,CI Y=0)
{
x=X; y=Y;
}
friend inline Complex operator + (const Complex& A,const Complex& B)
{
return Complex(sum(A.x,B.x),sum(A.y,B.y));
}
friend inline Complex operator - (const Complex& A,const Complex& B)
{
return Complex(sub(A.x,B.x),sub(A.y,B.y));
}
friend inline Complex operator * (const Complex& A,const Complex& B)
{
return Complex(sub(1LL*A.x*B.x%mod,1LL*A.y*B.y%mod),
sub(sum(1LL*A.x*B.y%mod,1LL*A.y*B.x%mod),1LL*A.y*B.y%mod));
}
}g[lim];
inline int quick_pow(int x,int p=mod-2,int mul=1)
{
for (;p;p>>=1,x=1LL*x*x%mod) if (p&1) mul=1LL*mul*x%mod; return mul;
}
inline Complex C_quick_pow(Complex x,int p,Complex mul=Complex(1,0))
{
for (;p;p>>=1,x=x*x) if (p&1) mul=mul*x; return mul;
}
namespace CT_Solver //Convolution_Transformation
{
inline Complex calc1(const Complex& A) //calc A*w
{
return Complex(mod-A.y,sub(A.x,A.y));
}
inline Complex calc2(const Complex& A) //calc A*w^2
{
return Complex(sub(A.y,A.x),mod-A.x);
}
inline void DFT(Complex *f)
{
RI mid,j,k; for (mid=1;mid<lim;mid*=3)
for (j=0;j<lim;j+=mid*3) for (k=0;k<mid;++k)
{
Complex x=f[j+k],y=f[j+k+mid],z=f[j+k+(mid<<1)];
f[j+k]=x+y+z; f[j+k+mid]=x+calc1(y)+calc2(z);
f[j+k+(mid<<1)]=x+calc2(y)+calc1(z);
}
}
inline void IDFT(Complex *f)
{
RI mid,j,k; for (mid=1;mid<lim;mid*=3)
for (j=0;j<lim;j+=mid*3) for (k=0;k<mid;++k)
{
Complex x=f[j+k],y=f[j+k+mid],z=f[j+k+(mid<<1)];
f[j+k]=x+y+z; f[j+k+mid]=x+calc2(y)+calc1(z);
f[j+k+(mid<<1)]=x+calc1(y)+calc2(z);
}
int Iv=quick_pow(lim); for (RI i=0;i<lim;++i) f[i].x=1LL*f[i].x*Iv%mod;
}
};
#define Pj prime[j]
inline void init(CI n)
{
vis[1]=1; for (RI i=2,j;i<=n;++i)
{
if (!vis[i]) prime[++cnt]=i;
for (j=1;j<=cnt&&i*Pj<=n;++j)
{
vis[i*Pj]=1; if (i%Pj==0) break;
}
}
}
inline int resolve(int x,int ret=1)
{
for (RI j=1;j<=cnt&&Pj*Pj<=x;++j) if (x%Pj==0)
{
int cur=0; while (x%Pj==0) ++cur,x/=Pj;
ret=ret*(cur+1);
}
if (x>1) ret*=2; --ret;
int bs=1,ans=0; for (;ret;ret>>=1,bs*=3) if (ret&1) ans+=bs;
return ans;
}
#undef Pj
int main()
{
//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
for (init(S),scanf("%d",&t);t;--t)
{
RI i; for (scanf("%d%d",&n,&k),i=1;i<=n;++i)
scanf("%d",&x),++g[resolve(x)].x;
for (CT_Solver::DFT(g),i=0;i<lim;++i) g[i]=C_quick_pow(g[i],k);
CT_Solver::IDFT(g); printf("%d
",sub(quick_pow(n,k),g[0].x));
memset(g,0,sizeof(g));
}
}
Pretty Boxes
只会一个暴力费用流以及一个完全不知道正确性的模拟费用流(还不知道怎么维护答案)
先讲一下费用流的做法吧,首先我们把所有盒子从按(s_i)第一关键字,(p_i)第二关键字排序
那么此时若要选取一对盒子(i,j(i<j))配对,贡献一定是(p_j-p_i)
那么我们考虑建出这样一个图:源点(S)向每个点(i)连((1,p_i))的边,同时每个点向汇点连((1,-p_i))的边,然后对于每个(iin [2,n]),向(i-1)连一条((infty,0))的边
所以现在的图大概长这样:
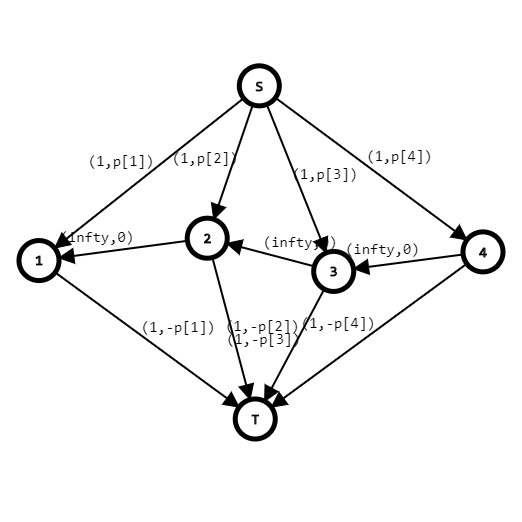
所以源点的流量就是选择的点对数,那么我们只要每次都能使源点的流量加(1)即可
那么又是一个小trick,我们再搞一个超级源点向(S)连边,每次在残量网络上将这条边流量加(1)即可
那么我们可以轻松地获得50pts的好成绩
#include<cstdio>
#include<queue>
#include<iostream>
#include<algorithm>
#define int long long
#define RI register int
#define CI const int&
using namespace std;
const int N=3005,INF=1e18;
struct edge
{
int to,nxt,v,c;
}e[N*6]; int n,head[N],cnt=1,s,t,ss,ans;
struct data
{
int s,p;
friend inline bool operator < (const data& A,const data& B)
{
return A.s<B.s||(A.s==B.s&&A.p<B.p);
}
}a[N];
inline void addedge(CI x,CI y,CI v,CI c)
{
e[++cnt]=(edge){y,head[x],v,c}; head[x]=cnt;
e[++cnt]=(edge){x,head[y],0,-c}; head[y]=cnt;
}
#define to e[i].to
class Network_Flow
{
private:
int pre[N],lst[N],cap[N],dis[N]; bool vis[N]; queue <int> q;
public:
inline bool SPFA(CI s,CI t)
{
RI i; for (i=s;i<=t;++i) pre[i]=-1,dis[i]=-INF;
q.push(s); dis[s]=0; vis[s]=1; cap[s]=INF;
while (!q.empty())
{
int now=q.front(); vis[now]=0; q.pop();
for (i=head[now];i;i=e[i].nxt)
if (e[i].v&&dis[to]<dis[now]+e[i].c)
{
dis[to]=dis[now]+e[i].c; cap[to]=min(cap[now],e[i].v);
pre[to]=now; lst[to]=i; if (!vis[to]) vis[to]=1,q.push(to);
}
}
return ~pre[t];
}
inline int MCMF(CI s,CI t)
{
++e[cnt^1].v; int ret=0; while (SPFA(s,t))
{
if (dis[t]<=0) break; ret+=cap[t]*dis[t];
for (int nw=t;nw!=s;nw=pre[nw])
e[lst[nw]].v-=cap[t],e[lst[nw]^1].v+=cap[t];
}
return ret;
}
}NF;
#undef to
signed main()
{
//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
RI i; for (scanf("%lld",&n),s=n+1,t=n+2,i=1;i<=n;++i)
scanf("%lld%lld",&a[i].s,&a[i].p); sort(a+1,a+n+1);
for (i=n;i>1;--i) addedge(i,i-1,INF,0);
for (i=1;i<=n;++i) addedge(s,i,1,a[i].p),addedge(i,t,1,-a[i].p);
for (addedge(ss,s,0,0),i=1;(i<<1)<=n;++i) printf("%lld
",ans+=NF.MCMF(ss,t));
return 0;
}
然后这里给一个我比赛的时候口胡的做法:
按序进行每一次配对。考虑对于每个没被选择的点(i),开一个堆记录下所有能放在它里面的(j)的(p_j)的(min)记为(q_i),以及对应的位置(nq_i)。还计算每一个堆中的(operatorname{second\_min})为(sq_i)
考虑每次找到(p_i-q_i)最大的一组((i,nq_i))计算答案,考虑未来的反悔操作:
- 一个能选择(i)的(j)拿走了(i),那么此时将(-sq_i-p_i+q_i)加入每个(j)的堆中
- 一个能选择(nq_i)的(j)拿走了(nq_i),那么此时将(-sq_i)加入每个(j)的堆中
重复上面的操作即可
但是维护区间的堆我根本写不来,直接GG
(Challenge) Coloring Triangulations
难得写了下Challenge的说。。。
刚开始码了个只改点颜色的贪心,然后30min就喜提12.1分
#include<cstdio>
#include<cstdlib>
#include<cstring>
#define RI register int
#define CI const int&
using namespace std;
const int N=520,M=1<<10|5,INF=1e9;
int n,m,cx,cy,p,q,x[N],y[N],tri[M][3],eg[N][N][2],sz[N][N],ret; char col[N],ans[N];
inline void addedge(CI x,CI y,CI id)
{
eg[x][y][++sz[x][y]]=eg[y][x][++sz[y][x]]=id;
}
inline int calc(int ret=0)
{
for (RI i=1,j,k;i<=m;++i)
{
bool flag=0; for (j=0;j<3;++j) for (k=j+1;k<3;++k)
if (col[tri[i][j]]==col[tri[i][k]]) { flag=1; break; }
ret+=flag;
}
return ret*ret;
}
inline char nxt_col(const char& ch)
{
if (ch=='R') return 'G'; if (ch=='G') return 'B'; return 'R';
}
inline bool miner(int& x,CI y)
{
if (y<=x) return x=y,1; return 0;
}
inline int recolor(void)
{
ret=calc(); RI i,j; int c=0; for (i=1;i<=p;++i)
{
int cur=INF,pos; char tp;
for (j=1;j<=n;++j)
{
col[j]=nxt_col(col[j]); if (miner(cur,calc())) pos=j,tp=col[j];
col[j]=nxt_col(col[j]); if (miner(cur,calc())) pos=j,tp=col[j];
col[j]=nxt_col(col[j]);
}
col[pos]=tp; if (cur+cx*i<ret) c=i,ret=cur+cx*i,memcpy(ans,col,sizeof(ans));
}
return c;
}
namespace Case1 //Only Recolor Point Solver
{
inline void solve(void)
{
int c=recolor(); printf("%d 0
%s",c,ans+1);
}
};
namespace Case2 //Random Edge Solver
{
};
int main()
{
//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
RI i,j,k; scanf("%d%d%d%d%d%d%s",&n,&m,&cx,&cy,&p,&q,col+1);
for (i=1;i<=n;++i) scanf("%d%d",&x[i],&y[i]); for (i=1;i<=m;++i)
{
scanf("%d%d%d",&tri[i][0],&tri[i][1],&tri[i][2]);
for (j=0;j<3;++j) for (k=j+1;k<3;++k) addedge(tri[i][j],tri[i][k],i);
}
//if (cx<=cy) Case1::solve(); else Case2::solve(); return 0;
return Case1::solve(),0;
}
然后我就又写了一个随机换边的代码,然后中间还重构代码了好几次。最后花了一个下午喜提12.7pts
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cmath>
#include<vector>
#define RI register int
#define CI const int&
#define Mc(a,b) memcpy(a,b,sizeof(a))
using namespace std;
typedef vector <int>:: iterator VI;
const int N=550,M=1<<10|5,T=5,INF=1e9;
const double pi=acos(-1);
bool ext[M]; char tcol[N],col[N],rans[N],ans[N];
vector <int> pv[N]; int n,m,cx,cy,ansc,ansf,ctf,odr[N][2],fodr[N][2];
int p,q,x[N],y[N],tri[M][3],t_tri[M][3],ct[N],ret,num,all;
inline int calc(int ret=0)
{
for (RI i=1,j,k;i<=m;++i)
{
bool flag=0; for (j=0;j<3;++j) for (k=j+1;k<3;++k)
if (col[tri[i][j]]==col[tri[i][k]]) { flag=1; break; }
ret+=(ext[i]=flag);
}
return ret;
}
inline int recalc(CI x,int ret=0)
{
for (VI it=pv[x].begin();it!=pv[x].end();++it)
{
bool flag=0; for (RI j=0,k;j<3;++j) for (k=j+1;k<3;++k)
if (col[tri[*it][j]]==col[tri[*it][k]]) { flag=1; break; }
if (ext[*it]&&!flag) --ret; if (!ext[*it]&&flag) ++ret; ext[*it]=flag;
}
return ret;
}
inline char lst_col(const char& ch)
{
if (ch=='R') return 'B'; if (ch=='G') return 'R'; return 'G';
}
inline char nxt_col(const char& ch)
{
if (ch=='R') return 'G'; if (ch=='G') return 'B'; return 'R';
}
inline bool miner(int& x,CI y)
{
if (y<=x) return x=y,1; return 0;
}
inline int recolor(void)
{
Mc(col,tcol); num=calc(); ret=num*num; RI i,j; int c=0; for (i=1;i<=n;++i) pv[i].clear();
for (i=1;i<=m;++i) for (j=0;j<3;++j) pv[tri[i][j]].push_back(i);
for (i=1;i<=p;++i)
{
int cur=INF,pos; char tp;
for (j=1;j<=n;++j)
{
col[j]=nxt_col(col[j]); if (miner(cur,num+recalc(j))) pos=j,tp=col[j];
col[j]=lst_col(col[j]); recalc(j); col[j]=nxt_col(col[j]);
col[j]=nxt_col(col[j]); if (miner(cur,num+recalc(j))) pos=j,tp=col[j];
col[j]=nxt_col(col[j]); recalc(j);
}
col[pos]=tp; num=cur; if (cur*cur+cx*i<ret) c=i,ret=cur*cur+cx*i,Mc(ans,col);
}
return c;
}
inline double dist(CI u,CI v)
{
return sqrt((x[u]-x[v])*(x[u]-x[v])+(y[u]-y[v])*(y[u]-y[v]));
}
inline int dist_2(CI u,CI v)
{
return (x[u]-x[v])*(x[u]-x[v])+(y[u]-y[v])*(y[u]-y[v]);
}
inline bool check(CI id1,CI id2,int& u,int& v,int& a,int& b)
{
RI i; int cur=0; for (i=0;i<3;++i) (!ct[tri[id1][i]]&&++cur),++ct[tri[id1][i]];
for (i=0;i<3;++i) (!ct[tri[id2][i]]&&++cur),++ct[tri[id2][i]];
if (cur!=4) { for (i=0;i<3;++i) ct[tri[id1][i]]=ct[tri[id2][i]]=0; return 0; }
for (i=0;i<3;++i) if (ct[tri[id1][i]]==2) { u=tri[id1][i]; break; }
for (++i;i<3;++i) if (ct[tri[id1][i]]==2) { v=tri[id1][i]; break; }
for (i=0;i<3;++i) if (ct[tri[id1][i]]==1) { a=tri[id1][i]; break; }
for (i=0;i<3;++i) if (ct[tri[id2][i]]==1) { b=tri[id2][i]; break; }
for (i=0;i<3;++i) ct[tri[id1][i]]=ct[tri[id2][i]]=0;
if (acos(1.0*(dist_2(u,v)+dist_2(u,a)-dist_2(a,v))/(2.0*dist(u,v)*dist(u,a)))+
acos(1.0*(dist_2(u,v)+dist_2(u,b)-dist_2(b,v))/(2.0*dist(u,v)*dist(u,b)))>pi) return 0;
if (acos(1.0*(dist_2(v,u)+dist_2(v,a)-dist_2(a,u))/(2.0*dist(v,u)*dist(v,a)))+
acos(1.0*(dist_2(v,u)+dist_2(v,b)-dist_2(b,u))/(2.0*dist(v,u)*dist(v,b)))>pi) return 0;
return 1;
}
inline void reflip(void)
{
Mc(tri,t_tri); ctf=0; for (RI i=1,j,k;i<=50;++i)
{
int id1=rand()%m+1,id2=rand()%m+1,u,v,a,b;
while (!check(id1,id2,u,v,a,b)) id1=rand()%m+1,id2=rand()%m+1; odr[++ctf][0]=u; odr[ctf][1]=v;
tri[id1][0]=tri[id2][0]=a; tri[id1][1]=tri[id2][1]=b; tri[id1][2]=u; tri[id2][2]=v;
int tp=recolor(); if (ret+cy*i<all) ansc=tp,all=ret+cy*i,ansf=ctf,Mc(rans,ans),Mc(fodr,odr);
}
}
int main()
{
//freopen("CODE.in","r",stdin); freopen("CODE.out","w",stdout);
RI i,j,k; scanf("%d%d%d%d%d%d%s",&n,&m,&cx,&cy,&p,&q,col+1);
for (i=1;i<=n;++i) scanf("%d%d",&x[i],&y[i]);
for (srand(20030909),i=1;i<=m;++i) for (j=0;j<3;++j) scanf("%d",&tri[i][j]);
Mc(tcol,col); Mc(t_tri,tri); ansc=recolor(); all=ret; Mc(rans,ans);
reflip(); printf("%d %d
%s
",ansc,ansf,rans+1);
for (i=1;i<=ansf;++i) printf("%d %d
",fodr[i][0],fodr[i][1]);
return 0;
}
PS:我以后再刚Challenge我就是狗!
D-Dart
根本不会,连30pts的暴力都不会写……
Postscript
最后还是喜提Rank18涨了164Ranting,美滋滋……