今天是10班在一起的最后一天,但还是要在机房度过,哎...整个人都不好了,terrible...
所以今天根本不想做题,特别又全都是数学题...
testA想过dp,写的时候各种问题,一怒之下就打了个表...不过我还是很良心的,因为电脑太渣,只打了60kb...→_→50分,比某个打了6000kb+的人还多...
然后我一直再想testB,手算了几个数据,想dp来着,最后跪了...特判有30...
testC最大的困难就在于,看!不!懂!题!啊!啊!啊!啊!啊!啊!啊!啊!啊!
-----------------------------------------------------------------------------
testA
输入文件: testA.in 输出文件 :testA.out 时限:2000ms
问题描述:
如果一个数化为一个二进制数之后(没有前导0),0的个数>=1的个数。那么这个数就是方数。
Eg.(12)10 = (1100)2 2个1和2个0 所以12是一个方数。
(6)10=(110)2 2个1和1个0所以6不是一个方数。
现在方老师想知道区间[L,R]里有多少个方数。
输入描述:
一共一行L和R。(1<=L<=R<=2*10^9)
输出描述:
一个数表示[L,R]里有多少个方数。
数据范围 N<=200 , W<=100000 , M<=19900
样例输入:
2 12
样例输出:
6
题解:
比dp更简单简洁的方法,组合数!//还记得SmallFat机智的解释那个线性推的公式~
1 #define NOMBRE "testA"
2 #include <cstdio>
3 #include <cstring>
4
5 const int MAXN = 40;
6
7 int L, R, p[MAXN+10], c[MAXN+10][MAXN+10];
8
9 inline int Get(int x){
10 if (!x) return 0;
11 int len = 0, ret = 0, a0 = 0, a1 = 1;
12 memset(p, 0, sizeof(p));
13 while (x)
14 p[len++] = x&1, x >>= 1;
15 for (int ls=0; ls<len-1; ls++)
16 for (int z=ls; z>=0 && z>=ls-z+1; z--)
17 ret += c[ls][z];
18
19 for (int i=len-2; i>=0; i--)
20 if (p[i]){
21 a0 = len-i-a1;
22 for (int j=i; j>=0 && a0+j>=a1+i-j; j--)
23 ret += c[i][j];
24 a1 ++;
25 }
26 return (len-a1>=a1) ? ret+1 : ret;//check itself
27 }
28
29 inline void init(){
30 memset(c, 0, sizeof(c));
31 for (int i=0; i<MAXN; i++)
32 c[i][i] = c[i][0] = 1;
33 for (int i=2; i<MAXN; i++)
34 for (int j=1; j<i; j++)
35 c[i][j] = c[i-1][j]+c[i-1][j-1];
36 }
37
38 int main(){
39 freopen(NOMBRE ".in", "r", stdin);
40 freopen(NOMBRE ".out", "w", stdout);
41
42 init();
43 scanf("%d %d", &L, &R);
44 printf("%d
", Get(R)-Get(L-1));
45 }
-----------------------------------------------------------------------------
testB
输入文件: testB.in 输出文件testB.out 时限3000ms
问题描述:
定义这样一个序列(a1,b1),(a2,b2),…,(ak,bk)如果这个序列是方序列的话必须满足下面两个条件:
(1)1<=a1<=b1<a2<=b2<….<ak<=bk<=n 。其中n是给定的正整数。
(2)b1-a1,b2-a2,….,bk-ak两两互不相同。
现在方老师想知道给定n的情况下有多少种不同的长度为k的方序列。
输入描述:
第一行一个数t表示有t组测试数据。(t<=2*10^5)
第二行至第t+1行每行两个数n和k。(1<=k<=1000 , 1<=n<=1000)
输出描述:
一共t行,每一行表示一个答案。
样例输入:
6
1 1
2 1
2 2
3 1
3 2
3 3
样例输出:
1
3
0
6
2
0
题解:
因为ai-bi的值不同,所以可以看成一个背包。由于n<=1000,物品大小就是[0, 50];
然后就可以推出公式(借用一下zyj那个美丽的图)
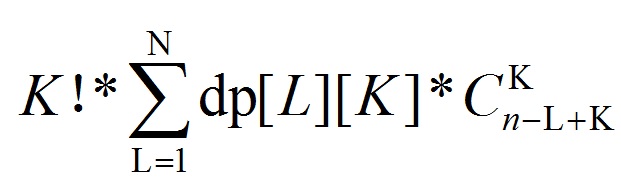
其中dp[j][k]表示在i位,选了k个,其和为j。//dp那部分是ysy给我讲的@Mrs.General
1 #define NOMBRE "testB"
2 #include <cstdio>
3 #include <cstring>
4 #include <algorithm>
5 using namespace std;
6
7 const int MOD = 1000000007;
8 const int MAXN = 1000;
9
10 int n, k, T;
11 long long dp[MAXN+10][MAXN+10], c[MAXN+10][MAXN+10], fac[MAXN+10];
12
13 inline void init(){
14 memset(c, 0, sizeof(c));
15 for (register int i=0; i<=MAXN; i++)
16 c[i][i] = c[i][0] = 1;
17 for (register int i=2; i<=MAXN; i++)
18 for (register int j=1; j<i; j++)
19 c[i][j] = (c[i-1][j]+c[i-1][j-1])%MOD;
20
21 fac[0] = 1;
22 for (int i=1; i<=MAXN; i++)
23 fac[i] = fac[i-1]*i%MOD;
24
25 dp[0][0] = dp[0][1] = 1;
26 for (register int i=1; i<=MAXN; i++)
27 for (register int k=50; k>=1; k--)
28 for (register int s=MAXN; s>=i; s--)
29 dp[s][k] = (dp[s-i][k-1]+dp[s][k])%MOD;
30 }
31
32 inline int Solve(){
33 if (n<k) return 0;
34 int ret = 0;
35 long long temp;
36 for (int l=0; l<=n-k; l++)
37 temp = (long long)c[n-l][k]*dp[l][k]%MOD,
38 ret = (temp+ret)%MOD;
39 ret = (ret*fac[k])%MOD;
40 return ret;
41 }
42
43 int main(){
44 freopen(NOMBRE ".in", "r", stdin);
45 freopen(NOMBRE ".out", "w", stdout);
46
47 init();
48 scanf("%d", &T);
49 while (T--)
50 scanf("%d %d", &n, &k), printf("%d
", Solve());
51 }
-----------------------------------------------------------------------------
testC
输入文件: testC.in 输出文件: testC.out 时限: 1000ms
问题描述:
给定一个n*m的国际象棋棋盘(左上角那个格子是黑的),方老师在第0时刻我们把所有的黑色格子全部重新涂成0号颜色,在第i个时刻方老师会把一些点(如果4个和他有恰好有一个公共顶点的格子都涂上的是i-1号颜色)重新涂成i号颜色(这种循环会无限进行下去,而且每次重新涂颜色是同时进行的)。最后问有多少个格子恰好被重新涂了x次。
输入描述:
一行三个数n,m,x。(1<=n,m<=5000,x<=10^9)
输出描述:
一个数表示有多少个格子被重新涂了x次
样例输入:
3 3
1
样例输出:
4
题解:
你得看懂题之后,就没有然后了
1 #define NOMBRE "testC"
2 #include <cstdio>
3
4 int N, M, cj, Pri;
5
6 int main(){
7 freopen(NOMBRE ".in", "r", stdin);
8 freopen(NOMBRE ".out", "w", stdout);
9
10 scanf("%d %d %d", &N, &M, &cj);
11 cj --, cj <<= 1, cj ++;
12 if (N<cj || M<cj) Pri = 0;
13 else if (N==cj) Pri = (M-cj+2)/2;
14 else if (M==cj) Pri = (N-cj+2)/2;
15 else Pri = N+M-2*cj;
16 printf("%d
", Pri);
17 }