【SDOI2017】天才黑客

题面

题解

这是好久之前菊开讲的一道题目了。

可以发现在这道题目中，边比点更加重要，所以我们化边为点，将边权改为点权，边与边之间的边权就是题目所给的Trie树上LCA深度的和。

想到一个平方的暴力，每条边和它连向的点的出边连一条边。下一步考虑怎么优化。

对于每一个点，将它的入边和出边都拿出来，按照dfs序排序，那么可以考虑将每个点拆成入点和出点，因为(operatorname{lcp}(i, j))的值是(i o j)之间所有的边的(operatorname{lcp})的最小值，于是前后缀优化连边就可以了。

可以考虑使用下面这个图来帮助理解：

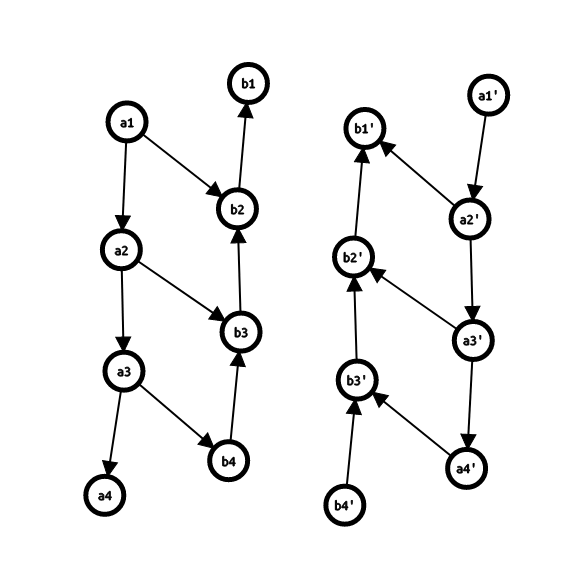
说起来容易做起来难，代码留给读者作为练习

代码

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
#define file(x) freopen(#x".in", "r", stdin), freopen(#x".out", "w", stdout)

inline int read()
{
	int data = 0, w = 1; char ch = getchar();
	while (ch != '-' && (ch < '0' || ch > '9')) ch = getchar();
	if (ch == '-') w = -1, ch = getchar();
	while (ch >= '0' && ch <= '9') data = data * 10 + (ch ^ 48), ch = getchar();
	return data * w;
}

const int N(50010);
struct edge { int to, dis; };
int T, n, m, K, val[N * 20], pos[N], dis[N * 20], vis[N * 20], cur;
std::vector<int> in[N], out[N];
std::vector<edge> G[N * 20];
namespace Tree
{
	int fa[N], size[N], heavy[N], dfn[N], bel[N], dep[N], cnt; std::vector<int> T[N];
	inline void Add(int x, int y) { T[x].push_back(y); }
	void dfs(int x)
	{
		size[x] = 1, heavy[x] = 0;
		for (auto i : T[x])
		{
			fa[i] = x, dep[i] = dep[x] + 1, dfs(i), size[x] += size[i];
			if (size[heavy[x]] < size[i]) heavy[x] = i;
		}
	}

	void dfs(int x, int chain)
	{
		dfn[x] = ++cnt, bel[x] = chain;
		if (heavy[x]) dfs(heavy[x], chain);
		for (auto i : T[x]) if (i != heavy[x]) dfs(i, i);
	}

	int LCA(int x, int y)
	{
		for (; bel[x] != bel[y]; x = fa[bel[x]])
			if (dfn[bel[x]] < dfn[bel[y]]) std::swap(x, y);
		return dfn[x] < dfn[y] ? dep[x] : dep[y];
	}
}

void Dijkstra()
{
	std::priority_queue<std::pair<int, int>, std::vector<std::pair<int, int> >,
		std::greater<std::pair<int, int> > > Q;
	memset(dis, 127, (cur + 1) << 2), memset(vis, 0, sizeof vis);
	for (auto i : out[1]) Q.push(std::make_pair(dis[i] = val[i], i));
	while (!Q.empty())
	{
		int x = Q.top().second; Q.pop(); if (vis[x]) continue; vis[x] = 1;
		for (auto i : G[x]) if (dis[x] + val[i.to] + i.dis < dis[i.to])
			Q.push(std::make_pair(dis[i.to] = dis[x] + val[i.to] + i.dis, i.to));
	}
}

int Abs(int x) { return x < 0 ? -x : x; }
int cmp(int x, int y) { return Tree::dfn[pos[Abs(x)]] < Tree::dfn[pos[Abs(y)]]; }
void Link(int x)
{
	static int stk[N], p1[N], p2[N], q1[N], q2[N]; int top = 0;
	for (auto i : in[x]) stk[++top] = i;
	for (auto i : out[x]) stk[++top] = -i;
	std::sort(stk + 1, stk + top + 1, cmp);
	for (int i = 1; i <= top; i++)
		p1[i] = ++cur, p2[i] = ++cur, q1[i] = ++cur, q2[i] = ++cur;
	for (int i = 2; i <= top; i++)
		G[p1[i - 1]].push_back((edge) {p1[i], 0}),
		G[q1[i - 1]].push_back((edge) {q1[i], 0}),
		G[p2[i]].push_back((edge) {p2[i - 1], 0}),
		G[q2[i]].push_back((edge) {q2[i - 1], 0});
	for (int i = 1; i <= top; i++)
		if (stk[i] > 0) G[stk[i]].push_back((edge) {p1[i], 0}),
						G[stk[i]].push_back((edge) {p2[i], 0});
		else stk[i] = -stk[i], G[q1[i]].push_back((edge) {stk[i], 0}),
							   G[q2[i]].push_back((edge) {stk[i], 0});
	for (int i = 1, x; i < top; i++)
		x = Tree::LCA(pos[stk[i]], pos[stk[i + 1]]),
		G[p1[i]].push_back((edge) {q1[i + 1], x}),
		G[p2[i + 1]].push_back((edge) {q2[i], x});
}

int main()
{
#ifndef ONLINE_JUDGE
	file(cpp);
#endif
	for (T = read(); T--; )
	{
		n = read(), m = cur = read(), K = read();
		memset(val, 0, sizeof val), Tree::cnt = 0;
		for (int i = 1, x, y; i <= m; i++)
			x = read(), y = read(), val[i] = read(), pos[i] = read(),
			out[x].push_back(i), in[y].push_back(i);
		for (int i = 1, x, y; i < K; i++)
			x = read(), y = read(), read(), Tree::Add(x, y);
		Tree::dfs(1), Tree::dfs(1, 1);
		for (int i = 2; i <= n; i++) Link(i);
		Dijkstra();
		for (int i = 2; i <= n; i++)
		{
			int ans = 2e9;
			for (auto x : in[i]) ans = std::min(ans, dis[x]);
			printf("%d
", ans);
		}
		for (int i = 1; i <= cur; i++) G[i].clear();
		for (int i = 1; i <= n; i++) in[i].clear(), out[i].clear();
		for (int i = 1; i <= K; i++) Tree::T[i].clear();
	}
	return 0;
}