定义
红黑树(red-black tree)是一种改进的二叉查找树,结点域中增加颜色属性(红或黑)。
二叉查找树的一般操作的时间为 O(lgn)。但若它退化成一棵n个结点的线性链后,操作最坏时间为
O(n)。而红黑树增加了着色和相关性质保证了查找、插入、删除的时间复杂度最坏为 O(lgn).
特征
- 每个节点非红即黑
- 根结点为黑
- 叶节点为黑
- 红色结点的孩子都为黑色结点
- 从任意结点到其子树中每个叶子节点的路径上包含相同数量的黑色结点
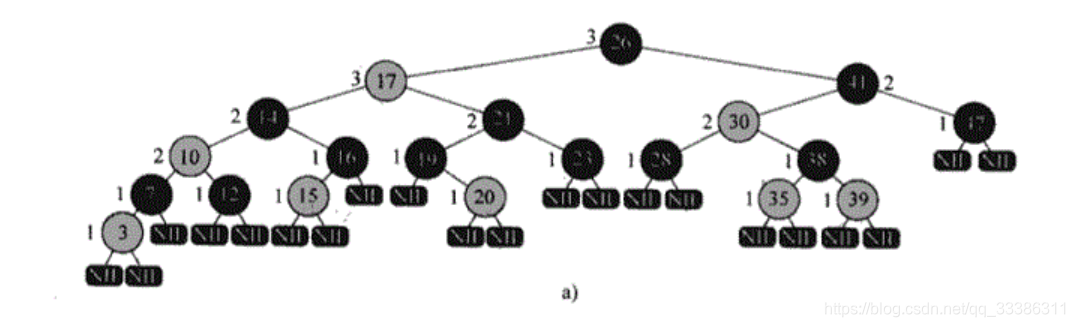
红黑树和234树是一种等价的数据结构
性质
- n个内结点的红黑树的高度最多为2lg(n+1)
- 黑高度为从某个结点出发(不包括该结点,包含叶子)到达一个叶结点的任意一 条路径上,黑色结点的个数,
记为bh(x)。 - 黑高度为k的红黑树,总结点数最多2(2k+1)-1个,内结点最多2(2k)-1(满二叉,红黑交替)。
内部结点数最少2^k-1(满二叉,全黑)。 - 某结点x到其后代结点的所有简单路径中,最长路径最多是最短路径的2倍。
参考https://blog.csdn.net/lanchunhui/article/details/75905478
旋转
红黑树上的search、minimum、maximum、successor、predecessor 可以在 O(logn)内完成。
时间复杂度O(1)

left-rotate(T,x)
y=right[x]
right[x]=left[x]
p[left[y]]=x
p[y]=p[x]
if p[x]=nil
root[T]=y
else if x=left[p[x]]
left[p[x]]Åy
else right[p[x]]=y
left[y]=x
p[x]=y
jdk8 TreeMap右旋源代码
/** From CLR */
private void rotateRight(Entry<K,V> p) {
if (p != null) {
Entry<K,V> l = p.left;
p.left = l.right;
if (l.right != null) l.right.parent = p;
l.parent = p.parent;
if (p.parent == null)
root = l;
else if (p.parent.right == p)
p.parent.right = l;
else p.parent.left = l;
l.right = p;
p.parent = l;
}
}
插入
主要分两步:
- 首先和二叉查找树的插入一样,查找、插入。
- 然后调整结构,保证满足红黑树状态,对结点进行重新着色,以及对树进行相关的旋转操作。
二叉查找树的就是一个二分查找,找到合适的位置就放进去。红黑树的插入在二叉查找树插入的基础上,为了重新恢复平衡,继续做了插入修复操作。
当我们往红黑树中插入一个黑色节点时,会打破一个平衡:任一节点到它子树的每个叶子节点的路径中都包含同样数量的黑节点。
当我们给一个红色节点下插入一个红色节点时,会打破另一个平衡:红色节点的左右孩子一定都是黑色节点。
为了简化调整,我们直接把插入的节点直接染成红色,这样就不会影响上一个平衡,只要专心调整满足后一个平衡就好了。染成红色后,我们只要关心父节点是否为红,如果是红的,就要把父节点进行变化,让父节点变成黑色,或者换一个黑色节点当父亲,这些操作的同时不能影响 不同路径上的黑色节点数一致的规则。
关注插入节点的父亲节点的位置,而父亲节点位于其爷爷节点地左子树或者右子树的操作是相对称的,座椅只需要研究一侧,即插入位置的父亲节点为左子树。
插入、染红后的调整有 2 种情况:
情况1.父亲节点和叔叔节点都是红色
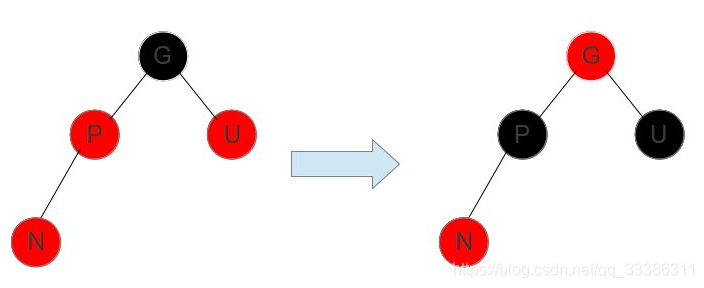
如上图所示,假设插入的是节点 N,这时父亲节点 P 和叔叔节点 U 都是红色,爷爷节点 G 一定是黑色。
红色节点的孩子不能是红色,这时不管 N 是 P 的左孩子还是右孩子,只要同时把 P 和 U 染成黑色,G 染成红色即可。这样这个子树左右两边黑色个数一致,也满足特征 4。
但是这样改变后 G 染成红色,G 的父亲如果是红色可能又违反特征 4 了,因此需要以 爷爷节点 G 为新的调整节点,再次进行循环调整操作,直到父亲节点不是红的。
情况2.父亲节点为红色,叔叔节点为黑色
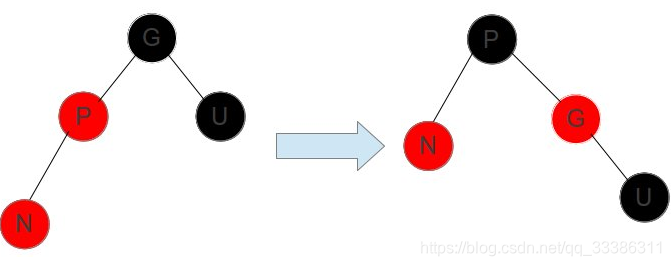
如上图所示,假设插入的是节点 N,这时父亲节点 P 是红色,叔叔节点 U 是黑色,爷爷节点 G 一定是黑色。
红色节点的孩子不能是红色,但是直接把父亲节点 P 涂成黑色也不行,这条路径多了个黑色节点。
通过把 爷爷节点 G 右旋,P 变成了这个子树的根节点,G 变成了 P 的右子树。
右旋后 G 跑到了右子树上,这时把 P 变成黑的,多了一个黑节点,再把 G 变成红的,就平衡了!
上面讲的是插入节点 N 在父亲节点 P 的左孩子位置,如果 N 是 P 的右孩子,就需要多进行一次左旋,把情况化解成上述情况,如下图:
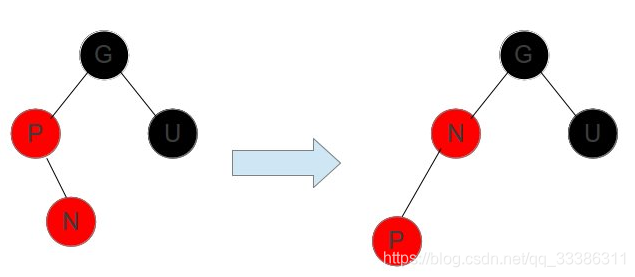
时间复杂度:O(lgn),最多两次旋转
4. 删除
O(lgn)最多三次旋转
5. 查找
O(lgn)
数据结构扩张
- 挑选一个合适的基本数据结构
- 决定在基本数据结构上增加的信息
- 修改基本数据结构上的操作并维持原有的性能
- 修改或设计新的操作
扩展结构
-
序统计树
序统计就是在一系列数中找出最大、最小值,某个数的序值等操作。
结点域增加size(以x为根的子树所包含的内部结点数,包括x)
操作的时间复杂度O(lgn) -
区间树O(lgn)
应用场景
- 广泛用于C++的STL中,map和set都是用红黑树实现的.
- 著名的Linux进程调度Completely Fair Scheduler,用红黑树管理进程控制块,进程的虚拟内存区域都存储在一颗红黑树上,每个虚拟地址区域都对应红黑树的一个节点,左指针指向相邻的地址虚拟存储区域,右指针指向相邻的高地址虚拟地址空间.
- IO多路复用epoll的实现采用红黑树组织管理sockfd,以支持快速的增删改查.
- Ngnix中,用红黑树管理timer,因为红黑树是有序的,可以很快的得到距离当前最小的定时器.
- Java中TreeMap的实现.
参考
《算法导论》
https://blog.csdn.net/lanchunhui/article/details/75905478
https://blog.csdn.net/u011240877/article/details/53329023
https://blog.csdn.net/whoamiyang/article/details/51926985