java排序

图片来自网络

一、用泛型实现快排，可以传入不通类型进行排序，比如String数组，Integer数组。

/**
 * 快速排序
 * 
 * @author chx
 *
 */
public class QuickSort {
    /**
     * 数组内数值的交换函数
     * 
     * @param arr
     *            原数组
     * @param leftIndex
     *            左索引
     * @param rightIndex
     *            右索引
     */
    private static <T> void change(T[] arr, int leftIndex, int rightIndex) {
        T temp = arr[leftIndex];
        arr[leftIndex] = arr[rightIndex];
        arr[rightIndex] = temp;
    }

    public static <T> void sort(T[] arr, int left, int right) {
        if (right < left) {
            // 查找区间内，外的返回
            return;
        }
        T flag = arr[left];// 哨兵的值
        int indexLeft = left;// 本轮查找需要的左索引
        int indexRight = right;// 本轮查找需要的右索引

        while (indexLeft != indexRight) {
            // 开始从右向左找，找比哨兵小的值。或者直到遇到左索引
            while (Integer.parseInt(arr[indexRight].toString()) >= Integer.parseInt(flag.toString())
                    && indexLeft < indexRight) {
                indexRight--;
            }
            // 从左向右找，找到比哨兵大的值，或者直到遇到右索引
            while (Integer.parseInt(arr[indexLeft].toString()) <= Integer.parseInt(flag.toString())
                    && indexLeft < indexRight) {
                indexLeft++;
            }
            if (indexLeft < indexRight) {
                // 找到了，交换
                change(arr, indexLeft, indexRight);
            }
        }
        // 此时一遍探索结束，将哨兵和当前的值进行交换，并进行分区探索
        change(arr, left, indexLeft);
        // 右边探索
        sort(arr, indexRight + 1, right);
        // 左边探索
        sort(arr, left, indexLeft - 1);
    }
}

 二、利用Arrays.sort()进行排序

　　突然有个同学咨询Arrays.sort用法，正好在此记录。

　　1.简介：有的时候不愿意去写排序程序，可以利用java自带的Arrays.sort()方法。

2.使用规则：总结为，基本数据类型直接放，引用数据类型需要利用实现了Comparator<T>的对象辅助排序。

3.具体用法：

package mianshi;

import java.util.Arrays;
import java.util.Comparator;

public class SortTest implements Comparator<SortTest> {
    private int sortValue;

    public int getSortValue() {
        return sortValue;
    }

    public void setSortValue(int sortValue) {
        this.sortValue = sortValue;
    }

    public static void main(String[] args) {
        SortTest[] list = new SortTest[5];

        for (int i = 0; i < list.length; i++) {
            list[i] = new SortTest();
            list[i].setSortValue(i*2);
        }

        Comparator<SortTest> cmp = new SortTest();
        Arrays.sort(list, cmp);

        for (int i = 0; i < list.length; i++) {
            System.out.print(list[i].getSortValue() + " ");
        }
    }

    @Override
    public int compare(SortTest o1, SortTest o2) {
        if (o1.getSortValue() > o2.getSortValue()) {
            return -1;
        }else if(o1.getSortValue() < o2.getSortValue()) {
            return 1;
        }

        return 0;
    }
}

返回值规则:compare是实现对比的方法，正数-大于，0-等于，负数-小于。所以本程序是倒序排序。

tips:感兴趣的可以百度下compare的实现原理、算法选择。有很多需要了解的内容。

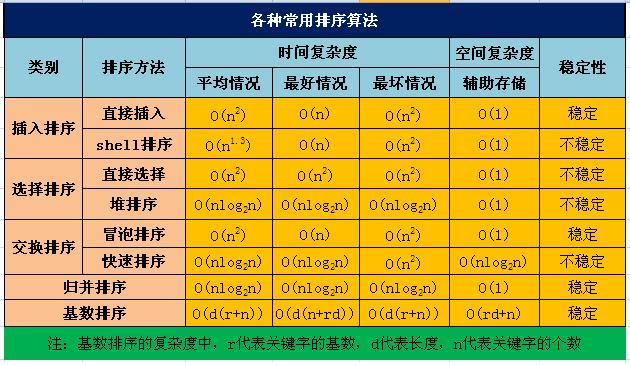
三、有关排序算法

//选择排序
public static void xuanZeSort(int[] arr) {
        for (int i = 0; i < arr.length; i++) {
            for (int j = i + 1; j < arr.length; j++) {
                if (arr[i] > arr[j]) {
                    int tmp = arr[i];
                    arr[i] = arr[j];
                    arr[j] = tmp;
                }
            }
        }
    }

 /**
     * 插入排序
     *
     * @param
     * @param arr
     * @return
     * @author chx
     * @date 2020/6/5 17:48
     */
    public static void insertSort(int[] arr) {
        //就一个核心思想。从第I个数开始向左找比其大(小)的位置index，期间全体右移。
        for (int i = 1; i < arr.length; i++) {
            int flag = arr[i];
            int j = i;

            while (j > 0 && flag < arr[j - 1]) {
                arr[j] = arr[j - 1];
                j--;
            }

            //此位置要么为0要么为找到的位置，由于一直右移，所以一定替换。
            arr[j] = flag;
        }
    }

/**
     * 希尔排序:真的只是对插入排序做了改善，代码及其相似。
     *
     * @param arr
     */
    public static void shellSort(int[] arr) {
        //增量因子这里可以百度，因子的选择有一定可能会影响效率。
        int step = arr.length / 3 + 1;
        //和插入排序多了一个while循环，当步长为0时表示排序完成。
        while (step > 0) {
            //从[步长位]开始，和所有第[i-步长]及[j-步长]比较，并进行移位。
            for (int i = step; i < arr.length; i++) {
                int flag = arr[i];
                int j = i - step;
                //和所有[j-step]位数值进行比较，
                while (j >= 0 && flag < arr[j]) {
                    //移位
                    arr[j + step] = arr[j];
                    j -= step;
                }

                arr[j + step] = flag;
            }

            step = (int) Math.floor(step / 3);
        }
    }

/**
     * 堆排序-大顶堆排序(升序)
     *
     * @param
     * @param arr
     * @return
     * @author chx
     * @date 2020/6/8 11:18
     */
    private static void bigHeapSort(int[] arr) {
        //将树的结构线性化，按照左子节点坐标=2*i+1，右子节点坐标=2*i+2。其中i表示坐标。
        //所以从最后一个非叶子节点开始(坐标为最大下标/2)，自左向右(自右向左)比较其叶子节点和其父节点大小。
        //确保父节点永远比叶子节点大(小顶堆找最小)，最终构建好的线性表即为大顶堆(其根节点是最大值)。其根节点要么最大要么最小。
        for (int i = arr.length / 2; i >= 0; i--) {
            changeHeapValue(arr, i, arr.length);
        }

        //创建完堆之后，对堆进行调整，每次调整把最大值放于根节点，并调换最后一个叶子节点和根节点，直到堆里只剩一个数据。
        int length = arr.length;

        for (int i = length - 1; i > 0; i--) {
            //交换根节点和最后一个子节点，这样就相当于把最大值取出来了。
            swap(arr, 0, i);
            //由于换了根节点和最后一个节点，所以重新排序。
            length--;
            changeHeapValue(arr, 0, length);
        }
    }


    /**
     * 交换两个下标的数值
     *
     * @param
     * @param arr       数组
     * @param index     下标A
     * @param swapIndex 下标B
     * @return
     * @author chx
     * @date 2020/6/8 11:41
     */
    private static void swap(int[] arr, int index, int swapIndex) {
        int tmp = arr[index];
        arr[index] = arr[swapIndex];
        arr[swapIndex] = tmp;
    }

    /**
     * 创建大顶堆过程中，比较父节点及其叶子节点的大小，进行改值操作。
     *
     * @param arr
     * @param index
     * @return
     * @author chx
     * @date 2020/6/8 12:07
     */
    private static void changeHeapValue(int[] arr, int index, int lenth) {
        int leftIndex = index * 2 + 1;
        int rightIndex = index * 2 + 2;
        int tmpIndex = index;

        //此处不用arr.length的原因是，后面对堆进行排序时会修改长度。因为最终堆只剩一个的时候就排序完了。
        if (leftIndex < lenth && arr[tmpIndex] < arr[leftIndex]) {
            //左子节点大于其父节点，记录，后面要交换。
            tmpIndex = leftIndex;
        }

        if (rightIndex < lenth && arr[tmpIndex] < arr[rightIndex]) {
            //右子节点大于其父节点，记录，后面进行交换。
            tmpIndex = rightIndex;
        }

        if (tmpIndex != index) {
            // 期间有改动，说明找到需要交换的值了，进行交换。
            swap(arr, index, tmpIndex);
            // 此子节点下继续探索，防止由于子父节点更换，导致原来子节点及其子节点的子节点 排列好的数据已经不符合大顶堆规则。
            changeHeapValue(arr, tmpIndex, lenth);
        }
    }

/**
     * 归并排序之递归实现
     */
    public static void mergeSortRecurrence(int[] arr, int left, int right) {
        //最小单位是两两比较，所以遇到1以下的就直接返回。
        if (left < right) {
            int mid = (left + right) / 2;
            //左边分割
            mergeSortRecurrence(arr, left, mid);
            //右边分割
            mergeSortRecurrence(arr, mid + 1, right);
            //合并排序
            mergeSortMerge(arr, left, mid, right);
        }
    }

    /**
     * 合并分割后的数组，并排序。最终会合为一个排序好的大数组。
     *
     * @param arr
     * @param left
     * @param mid
     * @param right
     */
    private static void mergeSortMerge(int[] arr, int left, int mid, int right) {
        //创建一个临时数组，用左数组的值与右数组的比较，由于左右两边都是有序的，所以才能保证放进临时数组的都是正确的。
        int[] tmp = new int[arr.length];//辅助数组
        int p1 = left, p2 = mid + 1, k = left;//p1、p2是检测指针，k是存放指针

        while (p1 <= mid && p2 <= right) {
            if (arr[p1] <= arr[p2]){
                tmp[k++] = arr[p1++];
            }
            else{
                tmp[k++] = arr[p2++];
            }
        }

        while (p1 <= mid) tmp[k++] = arr[p1++];//如果左边未检测完，直接将后面所有元素加到合并的序列中
        while (p2 <= right) tmp[k++] = arr[p2++];//同上

        //复制回原素组
        for (int i = left; i <= right; i++) {
            arr[i] = tmp[i];
        }
    }