COJ 0248 HDNOIP201408生成树

HDNOIP201408生成树

难度级别： A； 编程语言：不限；运行时间限制：5000ms； 运行空间限制：262144KB； 代码长度限制：2000000B

试题描述

输入

第一行包括两个整数V，E，表示图的度数和图的边数接下来E行，每行包括4 个整数v1，v2，a(v1,v2), b(v1,v2),表示图中的v1,v2 两点之间有一条权值为a(v1,v2), b(v1,v2)的边。顶点的下标从0 开始标记，即0<=v1,v2<V。 

输出

仅一行，包含一个整数：F(T)的最小值。

输入示例

3 4
1 2 1 1
2 0 1 1
0 1 1 1
0 2 2 3

输出示例

4

其他说明

对于20%的数据，V<=10，E<=20
对于50%的数据，V<=50，E<=1000 
对于100%的数据，V<=300，E<=10000，1 ≤a_((v1,v2)), b_((v1,v2))≤ 1000

题解：最小乘积生成树的板子。

 设每个点有x,y两个权值，求一棵生成树，使得sigma(x[i])*sigma(y[i])最小。

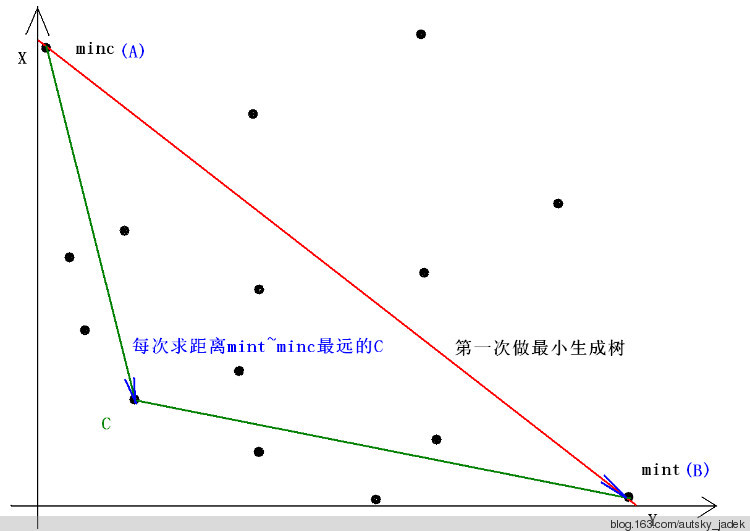
设每棵生成树为坐标系上的一个点，sigma(x[i])为横坐标，sigma(y[i])为纵坐标。则问题转化为求一个点，使得xy=k最小。即，使过这个点的反比例函数y=k/x最接近坐标轴。

Step1:求得分别距x轴和y轴最近的生成树（点）：A、B（分别按x权值和y权值做最小生成树即可）。

Step2:寻找一个在AB的靠近原点一侧的且离AB最远的生成树C，试图更新答案。

【怎么找？？？？

——由于C离AB最远，所以S△ABC面积最大。

向量AB=（B.x - A.x , B.y - A.y）

向量AC= (C.x - A.x , C.y - A.y)

向量AB、AC的叉积(的二分之一)为S△ABC的面积（只不过叉积是有向的，是负的，所以最小化这个值，即为最大化面积）。

最小化：(B.x-A.x)*(C.y-A.y)-(B.y-A.y)*(C.x-A.x)

=(B.x-A.x)*C.y+(A.y-B.y)*C.x  -  A.y*(B.x-A.x)+A.x*(B.y-A.y)/*粗体为常数，不要管*/

所以将每个点的权值修改为 y[i]*(B.x-A.x)+(A.y-B.y)*x[i] 做最小生成树，找到的即是C。】

Step3:递归地分别往AC、BC靠近原点的一侧找。递归边界：该侧没有点了(即叉积大于等于零)。——The Solution By AutSky_JadeK(From SDOI).http://www.cnblogs.com/autsky-jadek/.

#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<queue>
#include<cstring>
#define PAU putchar(' ')
#define ENT putchar('
')
using namespace std;
typedef long long ll;
const int maxn=300+10;
const int maxm=20000+10;
const int inf=1<<28;
inline long long read(){
    long long x=0,sig=1;char ch=getchar();
    while(!isdigit(ch)){if(ch=='-') sig=-1;ch=getchar();}
    while(isdigit(ch)) x=10*x+ch-'0',ch=getchar();
    return x*=sig;
}
inline void write(int x){
    if(x==0){putchar('0');return;}if(x<0) putchar('-'),x=-x;
    int len=0,buf[15];while(x) buf[len++]=x%10,x/=10;
    for(int i=len-1;i>=0;i--) putchar(buf[i]+'0');return;
}
struct point{ll x,y;}ans;
point operator-(const point&a,const point&b){return(point){a.x-b.x,a.y-b.y};}
ll operator*(point a,point b){return a.x*b.y-a.y*b.x;}
bool operator<(point a,point b){return a.x*a.y<b.x*b.y||a.x*a.y==b.x*b.y&&a.x<b.x;}
struct edge{int u,v,x,y;ll w;}e[maxm];
bool operator<(edge a,edge b){return a.w<b.w;}
int n,m,fa[maxn];
int findset(int x){return x==fa[x]?x:fa[x]=findset(fa[x]);}
void setinit(){for(int i=0;i<n;i++)fa[i]=i;return;}
point kruscal(){
    point tmp=(point){0,0};setinit(),sort(e,e+m);
    for(int i=0;i<m;i++){
        int u=findset(e[i].u),v=findset(e[i].v);
        if(u!=v){
            fa[u]=v;
            tmp.x+=e[i].x;
            tmp.y+=e[i].y;
        }
    }if(tmp<ans)ans=tmp;return tmp;
}
void solve(point a,point b){
    for(int i=0;i<m;i++)e[i].w=(b.x-a.x)*e[i].y+(a.y-b.y)*e[i].x;
    point c=kruscal();if((a-c)*(b-c)<0)solve(a,c),solve(c,b);return;
}
void init(){
    n=read(),m=read();
    for(int i=0;i<m;i++){
        e[i].u=read(),e[i].v=read();
        e[i].x=read(),e[i].y=read();
    }ans.x=ans.y=inf;
    return;
}
void work(){
    for(int i=0;i<m;i++)e[i].w=e[i].x;
    point a=kruscal();
    for(int i=0;i<m;i++)e[i].w=e[i].y;
    point b=kruscal();
    solve(a,b);
    return;
}
void print(){
    write(ans.x*ans.y);
    return;
}
int main(){init();work();print();return 0;}