课程:《Python程序设计》
班级: 1924
姓名: 陈瀚文
学号: 20192426
实验教师:王志强
实验日期:2020年4月16日
必修/选修: 公选课
1.实验内容
- 设计并完成一个完整的应用程序,完成加减乘除模等运算,功能多多益善。
- 考核基本语法、判定语句、循环语句、逻辑运算等知识点
2.实验过程及结果
实验过程:
第一版:
-
首先,想到计算器既可以直接计算出表达式的结果,又可以对得出的结果继续进行操作,因此分成两种情况:
-
进行新的运算
-
对得出的结果继续操作。
-
-
接下来,我使用while循环来让计算器可以进行多次计算。事实上,上文两种情况的差别并不是很大,完成一种情况,另一种情况也就接近完成了。于是,我便先完成了第一种情况的编写。
在这里我定义了judgesymbol()函数用来判断用户输入的操作符号是否为+-*/%
def judgesymbol(a):
if a in ["+", "-", "*", "/", "%", "**"]:
return 1
else:
print("�33[31m请重新输入运算符号!�33[0m")
return 0
定义了judgezero()函数来判断除数是否为0
def judgezero(a):
try:
eval(a)
return 1
except ZeroDivisionError:
print("�33[31m0不能作为除数!请重新输入!�33[0m")
return 0
这一部分的主体如下:
while True:
if i == 2:
a = input("请输入第一个操作数:")
s = input("请输入运算类型:")
if judgesymbol(s) == 0:
continue
b = input("请输入第二个操作数:")
sum = a+s+b
if judgezero(sum) == 0:
continue
print(sum+"={:g}".format(eval(sum)))
i = int(input("是否继续输入?(输入0结束,输入1对得出的结果继续操作,输入2进行新的运算)"))
这里我使用了eval()函数来计算表达式,并配合使用"{:g}".format()来使得结果不产生多余的零,使用i来作为循环的条件。
- 紧接着修改第一部分的代码,完成了第二部分。(代码中标注了发生变化的地方)
while True: if i == 1: 3 sum1 = sum 4 print("第一个操作数为", eval(sum1)) a = input("请输入运算类型:") if judgesymbol(a) == 0: continue b = input("请输入第二个操作数:") 9 sum1 = sum+a+b if judgezero(sum1) == 0: continue 12 print("{}".format(eval(sum))+a+b+"={:g}".format(eval(sum1))) 13 sum = sum1 14 i = int(input("是否继续输入?(输入0结束,输入1对得出的结果继续操作,输入2进行新的运算)")) - 最终第一版的代码如下(码云直达):
# -*- encoding: utf-8 -*-
'''
文件: Experiment2.py
时间: 2020/04/11 16:12:24
作者: 20192426 陈瀚文
'''
# 版本一
def judgesymbol(a):
'''
判断是否输入的符号是否为+-*/%中的一个
'''
if a in ["+", "-", "*", "/", "%", "**"]:
return 1
else:
print("�33[31m请重新输入运算符号!�33[0m")
return 0
def judgezero(a):
'''
功能:判断被除数是否为零,若不为零输出运算结果,否则重新输入
'''
try:
eval(a)
return 1
except ZeroDivisionError:
print("�33[31m0不能作为除数!请重新输入!�33[0m")
return 0
i = 2
sum = ""
sum1 = ""
while True:
if i == 0:
break
if i == 1: # 对得出的结果继续操作
sum1 = sum
print("第一个操作数为", eval(sum1))
a = input("请输入运算类型:")
if judgesymbol(a) == 0: # 判断符号是否合法
continue
b = input("请输入第二个操作数:")
sum1 = sum+a+b
if judgezero(sum1) == 0: # 判断是否进行了除0运算
continue
print("{}".format(eval(sum))+a+b+"={:g}".format(eval(sum1)))
sum = sum1
i = int(input("是否继续输入?(输入0结束,输入1对得出的结果继续操作,输入2进行新的运算)"))
if i == 2: # 对两个数进行运算
a = input("请输入第一个操作数:")
s = input("请输入运算类型:")
if judgesymbol(s) == 0: # 判断符号是否合法
continue
b = input("请输入第二个操作数:")
sum = a+s+b
if judgezero(sum) == 0: # 判断是否进行了除0运算
continue
print(sum+"={:g}".format(eval(sum)))
i = int(input("是否继续输入?(输入0结束,输入1对得出的结果继续操作,输入2进行新的运算)"))
- 运行结果如下:
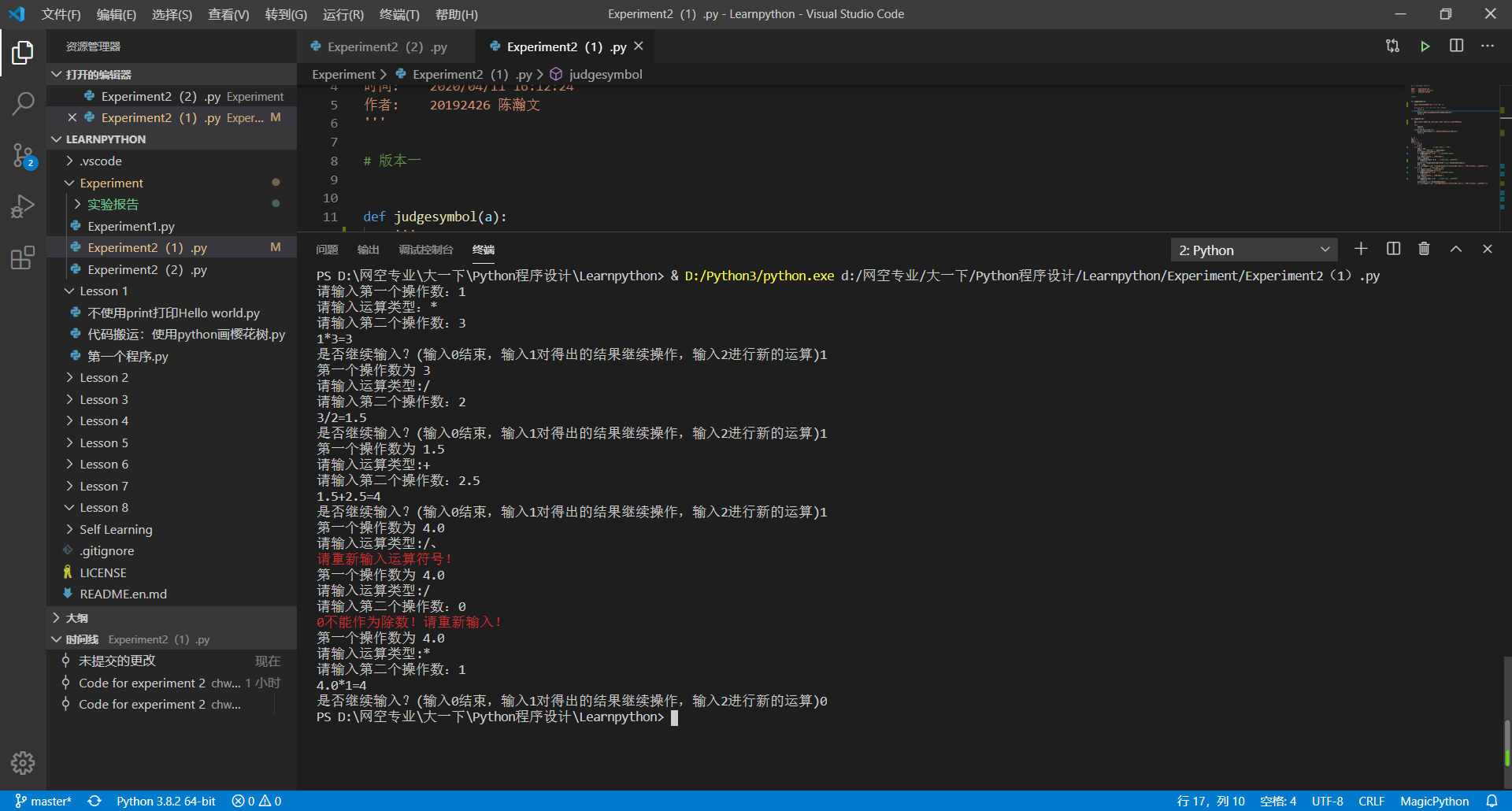
小结:在长期使用版本一的程序之后,我发现这个程序还有许多不足之处,例如在输入的时候操作数和表达式是分别输入的,如果输入错误还得重新输入,这就会用户导致浪费一些时间,从而使得程序的效率变得不高,使得程序在计算一些计算量不大的表达式时所耗费的时间长于心算的时间,给用户带来不便,因此我产生了优化程序的想法,并完成了第二版。
第二版(最终版)
- 对于第一版的代码,我做了如下思考:
- 应当将用户的输入过程进行简化,实现用户直接输入整个表达式便完成计算。
- 若用户直接将整个表达式输入,可以利用eval()函数直接求出表达式的值。
- 可以使用正则表达式来分割用户输入的字符串中的操作数和运算符,之后便可以根据分割得到的结果来进行分情况讨论。
- 这样一来,编写出计算三角函数的代码变得比较容易,可以给计算器加入计算三角函数的功能。 - 基于以上思考以及第一版的相关代码,我导入了re模块和math模块,并先完成四则运算部分的代码,定义了函数splitarg()从操作数与运算符中分离出非运算符部分
def splitarg(formula):
'''
功能:将数与运算符分离
'''
pattern = "[+-*/%]"
return re.split(pattern, formula)
定义函数splitmark()从操作数与运算符中分离运算符
def splitmark(formula):
'''
功能:将运算符与数分离
'''
pattern = "[0-9]"
mark = re.split(pattern, formula)
return list(filter(None, mark))
定义函数judge()判断被除数是否为零
def judge(formula):
'''
功能:判断被除数是否为零,若不为零输出运算结果,否则重新输入
'''
try:
print("{}={:g}".format(formula, eval(formula)))
return str(eval(formula))
except ZeroDivisionError:
print("�33[31m0不能作为除数!请重新输入!�33[0m")
-
在这之后,我参照版本一的代码完成了四则运算部分的函数编写,代码如下:
def simple(result): ''' 功能:四则运算+求余运算+乘方 ''' while True: formula = input() arg = splitarg(formula) # 把表达式以运算符为界分割成列表 arg = list(filter(None, arg)) # 将列表中的空字符串删掉 mark = splitmark(formula) # 把表达式中的运算符分离出来 if formula == "q": # 若输入为q,结束循环 print(" Bye~") return '0' elif formula == "c": # 若输入为c,切换成计算三角函数模式 return '2' elif len(arg) == 1 and mark != []: # 若输入的表达式只有一个操作数,则默认上一次计算的结果为另一个操作数 result = result+formula result = judge(result) else: # 正常输入表达式,正常计算 result = judge(formula) -
接着编写了三角函数部分,由于math模块提供的三角函数均使用弧度制,因而在三角函数运算时得先进行角度制转弧度制,在反三角函数运算时得将结果转换为角度制,故将两者分开考虑,代码如下:
def trigonometric(result): ''' 功能:计算三角函数 ''' while True: formula = input("请输入表达式:") if formula == "q": # 若输入为q,结束循环 print(" Bye~") return '0' elif formula == "c": # 若输入为c,切换成计算三角函数模式 return '1' else: arg = re.split("[()]", formula) # 将三角函数表达式以括号为界分割,组成列表 arg = list(filter(None, arg)) # 除去列表中的空字符串,若输入正确,此时列表的第一项为三角函数名,第二项为数据 # 判断表达式所计算的是三角函数还是反三角函数 if len(arg[0]) == 3: # 三角函数情况 arg[1] = eval(arg[1])/180*pi formula1 = eval(arg[0]+"("+str(arg[1])+")") print("{}={:g}".format(formula, formula1)) elif len(arg[0]) == 4: # 反三角函数情况 formula1 = eval(arg[0]+"("+str(arg[1])+")")*180/pi print("{}={:g}".format(formula, formula1)) -
至此,所需函数已全部编写完成,最后便是主函数部分。
print('''�33[36m---------------------开始计算---------------------�33[0m �33[33m--------------------输入q退出---------------------�33[0m ---------------请直接输入要计算的公式--------------- 支持运算类型: 1.四则运算 2.求余运算 3.乘方(用“**”表示,例如2^3表示为2**3) 4.三角函数计算(直接输入公式,例如:sin(x)) ''') mode = input('''请选择模式,输入对应的数字序号: 1.普通计算(对应类型1-3) 2.三角函数(对应类型4) 0.退出 ''') if mode == '0': print(" Bye~") while (int(mode)): # 当mode="0"时,程序退出 if mode == '1': # 当mode="1"时,执行四则运算函数 print("请输入表达式:(输入q退出,输入c切换模式)") result = "0" mode = simple(result) elif mode == '2': # 当mode="2"时,执行三角函数计算 print("请输入表达式:(角度使用角度制,反三角函数请使用形如asin()的形式输出输入q退出,输入c切换模式)") result = "0" mode = trigonometric(result) else: # 当输入其他值时,报错 print("�33[31m请正确输入模式序号!�33[0m") -
最终第二版代码如下(码云直达):
# -*- encoding: utf-8 -*-
'''
文件: Experiment2.py
时间: 2020/04/16 19:20:35
作者: 20192426 陈瀚文
'''
# 版本二
import re
from math import*
def splitarg(formula):
'''
功能:将数与运算符分离
'''
pattern = "[+-*/%]"
return re.split(pattern, formula)
def splitmark(formula):
'''
功能:将运算符与数分离
'''
pattern = "[0-9]"
mark = re.split(pattern, formula)
return list(filter(None, mark))
def judge(formula):
'''
功能:判断被除数是否为零,若不为零输出运算结果,否则重新输入
'''
try:
print("{}={:g}".format(formula, eval(formula)))
return str(eval(formula))
except ZeroDivisionError:
print("�33[31m0不能作为除数!请重新输入!�33[0m")
def simple(result):
'''
功能:四则运算+求余运算+乘方
'''
while True:
formula = input()
arg = splitarg(formula) # 把表达式以运算符为界分割成列表
arg = list(filter(None, arg)) # 将列表中的空字符串删掉
mark = splitmark(formula) # 把表达式中的运算符分离出来
if formula == "q": # 若输入为q,结束循环
print(" Bye~")
return '0'
elif formula == "c": # 若输入为c,切换成计算三角函数模式
return '2'
elif len(arg) == 1 and mark != []: # 若输入的表达式只有一个操作数,则默认上一次计算的结果为另一个操作数
result = result+formula
result = judge(result)
else: # 正常输入表达式,正常计算
result = judge(formula)
def trigonometric(result):
'''
功能:计算三角函数
'''
while True:
formula = input("请输入表达式:")
if formula == "q": # 若输入为q,结束循环
print(" Bye~")
return '0'
elif formula == "c": # 若输入为c,切换成计算三角函数模式
return '1'
else:
arg = re.split("[()]", formula) # 将三角函数表达式以括号为界分割,组成列表
arg = list(filter(None, arg)) # 除去列表中的空字符串,若输入正确,此时列表的第一项为三角函数名,第二项为数据
# 判断表达式所计算的是三角函数还是反三角函数
if len(arg[0]) == 3: # 三角函数情况
arg[1] = eval(arg[1])/180*pi
formula1 = eval(arg[0]+"("+str(arg[1])+")")
print("{}={:g}".format(formula, formula1))
elif len(arg[0]) == 4: # 反三角函数情况
formula1 = eval(arg[0]+"("+str(arg[1])+")")*180/pi
print("{}={:g}".format(formula, formula1))
print('''�33[36m---------------------开始计算---------------------�33[0m
�33[33m--------------------输入q退出---------------------�33[0m
---------------请直接输入要计算的公式---------------
支持运算类型:
1.四则运算
2.求余运算
3.乘方(用“**”表示,例如2^3表示为2**3)
4.三角函数计算(直接输入公式,例如:sin(x))
''')
mode = input('''请选择模式,输入对应的数字序号:
1.普通计算(对应类型1-3)
2.三角函数(对应类型4)
0.退出
''')
if mode == '0':
print(" Bye~")
while (int(mode)): # 当mode="0"时,程序退出
if mode == '1': # 当mode="1"时,执行四则运算函数
print("请输入表达式:(输入q退出,输入c切换模式)")
result = "0"
mode = simple(result)
elif mode == '2': # 当mode="2"时,执行三角函数计算
print("请输入表达式:(角度使用角度制,反三角函数请使用形如asin()的形式输出输入q退出,输入c切换模式)")
result = "0"
mode = trigonometric(result)
else: # 当输入其他值时,报错
print("�33[31m请正确输入模式序号!�33[0m")
- 运行结果如下
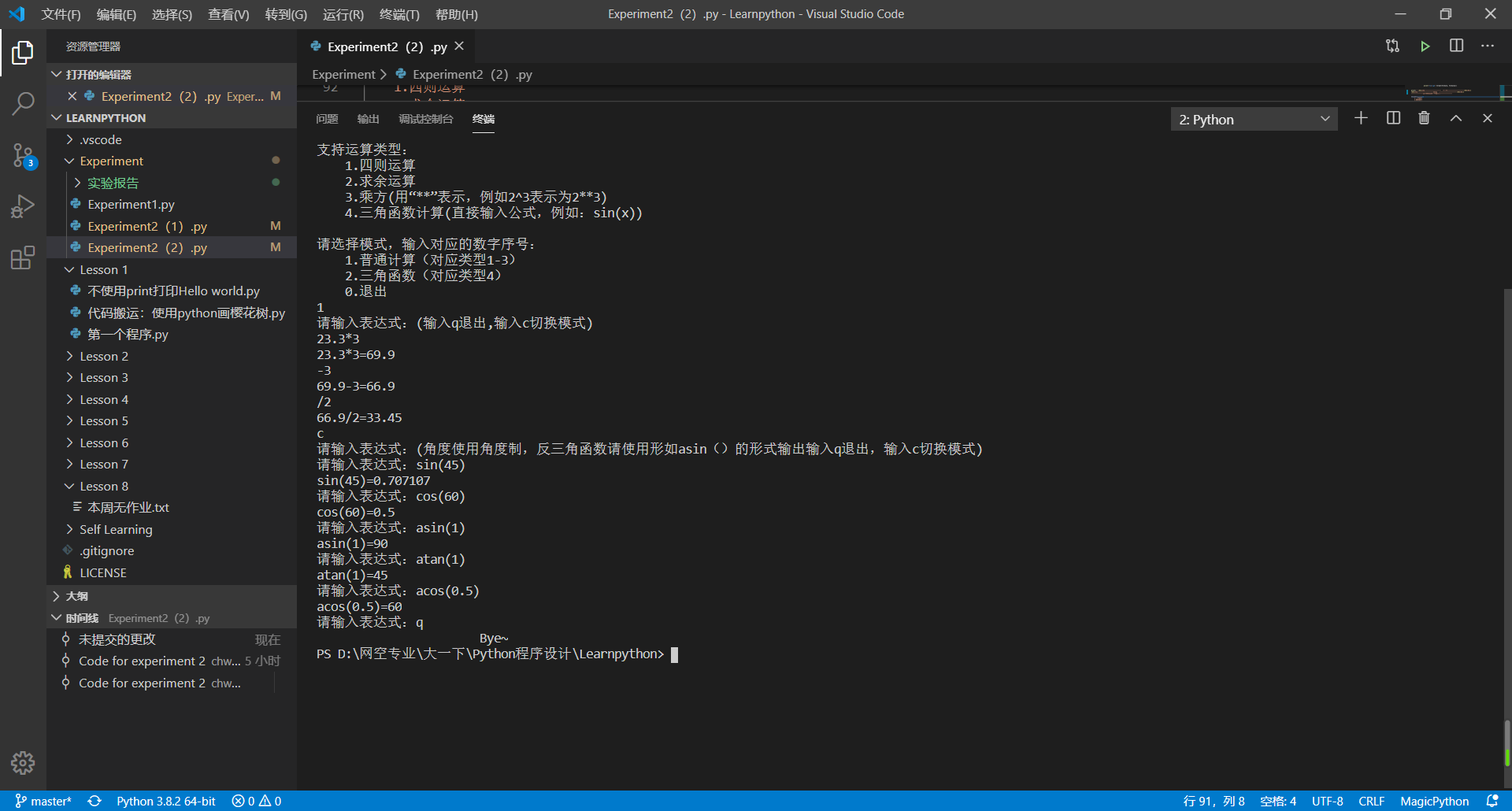
3. 实验过程中遇到的问题和解决过程
-
问题1:在编写完版本一的代码之后,发现输入过于繁琐,并不是非常方便
-
问题1解决方案:在版本一的基础上写出了版本二的代码,并添加了计算三角函数的功能
-
问题2:在编写计算三角函数的功能时由于没有考虑反三角函数与三角函数的区别而产生报错
-
问题2解决方案:使用if语句分别实现计算三角函数和反三角函数
-
问题3:在模式调整时,发现每次还会执行如下代码,造成不便
mode = input('''请选择模式,输入对应的数字序号:
1.普通计算(对应类型1-3)
2.三角函数(对应类型4)
0.退出
''')
- 问题3解决方案:将上述代码移到while循环的外面,解决了该问题
其他(感悟、思考等)
- 实验可以非常有效地检验学习的情况,在本次实验中我发现有一些知识我还是没有掌握牢固,同时我也发现当代码量达到一定程度之后,bug不会轻易被发现,修复bug变得十分困难,而调试功能则可以很好地让我清楚代码的哪个部分和设计的预期不相符,从而修复代码中的错误。
- 编写代码的过程应当多加思考,努力寻找更优的解决方法,提高程序的实用性。