Reference
LeetCode 322. 零钱兑换
labuladong的算法小抄
Markdown语法
Labuladong的算法小抄(纸质书籍 2021年1月第1版,2022年1月第七次印刷 第2章,第1节)
此问题解法和上一个斐波那契数列问题解法,我都会详细介绍解法原理,再后续动态规划算法原理和此相同,我只会解释题目解决方案窍门(即找到“状态”、“选择”和状态转移方程),不会再详细解释其他相关知识
动态规划一般解法
暴力穷举 -> 带备忘录的递归解法 -> dp 数组的迭代解法。
找到“状态”和“选择”->明确dp数组/函数的定义->寻找状态之间的关系。
难点
- dp数组的含义
- 寻找正确的状态转移方程(数学归纳法)
代码解释详见 Labuladong的算法小抄 书箱(2022年1月第七次印刷) pp.37-42
先看下题⽬:给你 k 种⾯值的硬币,⾯值分别为 c1, c2 ... ck,每种硬币的数量⽆限,再给⼀个总⾦额 amount ,问你最少需要⼏枚硬币凑出这个⾦额,如果不可能凑出,算法返回 -1。
算法的函数签名如下:

⽐如说k=3,⾯值分别为1,2,5,总⾦额amount=11。那么最少需要3枚硬币凑出,即11=5+5+1。
你认为计算机应该如何解决这个问题?显然,就是把所有肯能的凑硬币⽅法都穷举出来,然后找找看最少需要多少枚硬币。
⾸先,这个问题是动态规划问题,因为它具有「最优⼦结构」的。要符合「最优⼦结构」,⼦问题间必须互相独⽴。啥叫相互独⽴?你肯定不想看数学证明,我⽤⼀个直观的例⼦来讲解。
⽐如说,你的原问题是考出最⾼的总成绩,那么你的⼦问题就是要把语⽂考到最⾼,数学考到最⾼……为了每门课考到最⾼,你要把每门课相应的选择题分数拿到最⾼,填空题分数拿到最⾼……当然,最终就是你每门课都是满分,这就是最⾼的总成绩。
得到了正确的结果:最⾼的总成绩就是总分。因为这个过程符合最优⼦结构,“每门科⽬考到最⾼”这些⼦问题是互相独⽴,互不⼲扰的。
但是,如果加⼀个条件:你的语⽂成绩和数学成绩会互相制约,此消彼⻓。这样的话,显然你能考到的最⾼总成绩就达不到总分了,按刚才那个思路就会得到错误的结果。因为⼦问题并不独⽴,语⽂数学成绩⽆法同时最优,所以最优⼦结构被破坏。
回到凑零钱问题,为什么说它符合最优⼦结构呢?⽐如你想求amount=11时的最少硬币数(原问题),如果你知道凑出amount=10的最少硬币数(⼦问题),你只需要把⼦问题的答案加⼀(再选⼀枚⾯值为1的硬币)就是原问题的答案,因为硬币的数量是没有限制的,⼦问题之间没有相互制,是互相独⽴的。
那么,既然知道了这是个动态规划问题,就要思考如何列出正确的状态转移⽅程?
先确定「状态」,也就是原问题和⼦问题中变化的变量。由于硬币数量⽆限,所以唯⼀的状态就是⽬标⾦额amount。
然后确定 dp 函数的定义:当前的⽬标⾦额是 n ,⾄少需要dp(n)个硬币凑出该⾦额。
然后确定「选择」并择优,也就是对于每个状态,可以做出什么选择改变当前状态。具体到这个问题,⽆论当的⽬标⾦额是多少,选择就是从⾯额列表coins 中选择⼀个硬币,然后⽬标⾦额就会减少:
最后明确 base case,显然⽬标⾦额为 0 时,所需硬币数量为 0;当⽬标⾦额⼩于 0 时,⽆解,返回 -1:
方法1:暴力递归 (存在大量的重叠子问题)
递归问题最好都画出递归树,方法理解算法和计算时间空间复杂度
递归算法的时间复杂度:用子问题个数乘以解决一个子问题需要的时间。
⾄此,状态转移⽅程其实已经完成了,以上算法已经是暴⼒解法了,以上代码的数学形式就是状态转移⽅程:
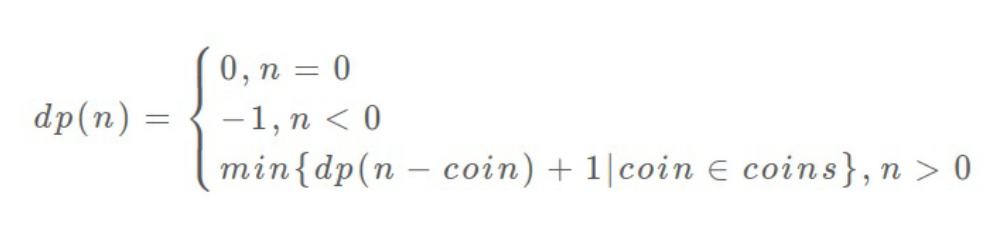
def func():
coins = list(map(int,input().strip().split()))
N = int(input())
def dp(coins,N):
if N == 0:
return 0
if N < 0:
return -1
res = float('inf')
for coin in coins:
subproblem = dp(coins,N-coin)
if subproblem == -1:
continue
res = min(res,1+subproblem)
return res if res != float('inf') else 0
return dp(coins,N)
if __name__ == '__main__':
c = func()
print(c)
⾄此,这个问题其实就解决了,只不过需要消除⼀下重叠⼦问题,⽐如 amount = 11, coins = {1,2,5} 时画出递归树看看:
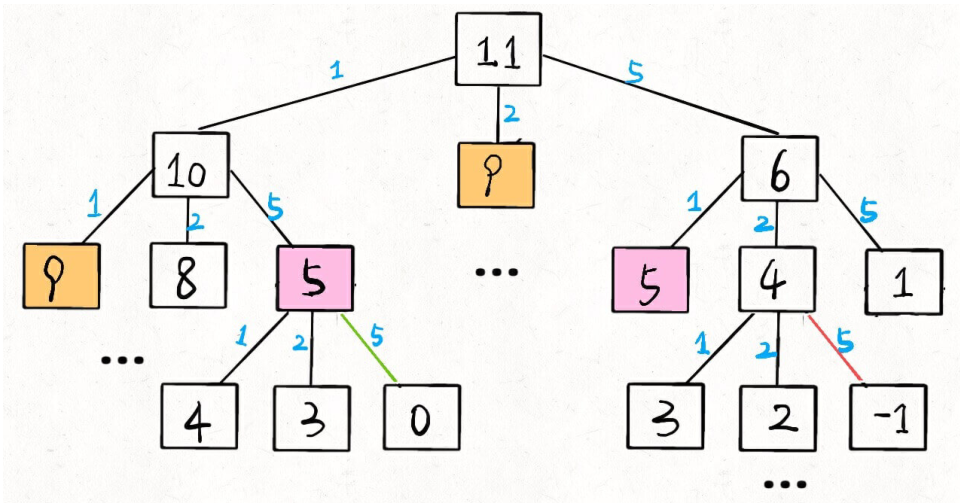
时间复杂度分析:⼦问题总数x每个⼦问题的时间。
⼦问题总数为递归树节点个数,这个⽐较难看出来,是O( n^k ),总之是指数级别的。每个⼦问题中含有⼀个for循环,复杂度为O(k)。所以总时间复杂度为O( k*n^k ),指数级别。
方法2:带备忘录的递归解法 (使用memo数组或者哈希表充当备忘录)
观察方法1的递归树,此方法相当于存在巨量冗余的递归二叉树,备忘录相当于提供了一套“剪枝”操作。使递归树改造成了一幅不存在冗余的递归树。极大地减少了子问题
只需要稍加修改,就可以通过备忘录消除⼦问题:
def func():
coins = list(map(int,input().strip().split()))
N = int(input())
def dp(coins,N):
memo = {} #定义哈希表
return helper(coins,N,memo)
def helper(coins,N,memo):
if N == 0:
memo[N] = 0
return memo[N]
if N < 0:
memo[N] = -1
return memo[N]
if N in memo.keys():
return memo[N]
res = float('inf')
for coin in coins:
subproblem = helper(coins,N-coin,memo)
if subproblem == -1:
continue
res = min(res, 1 + subproblem)
memo[N] = res if res != float('inf') else 0
return memo[N]
return dp(coins,N)
if __name__ == '__main__':
c = func()
print(c)
不画图了,很显然「备忘录」⼤⼤减⼩了⼦问题数⽬,完全消除了⼦问题的冗余,所以⼦问题总数不会超过⾦额数n,即⼦问题数⽬为O(n)。处理⼀个⼦问题的时间不变,仍是O(k),所以总的时间复杂度是O(kn)。
方法3:dp数组的迭代解法 (DP table 自底向上解法)
当然,我们也可以⾃底向上使⽤dptable来消除重叠⼦问题,dp数组的定义和刚才dp函数类似,定义也是⼀样的:
dp[i]=x表⽰,当⽬标⾦额为i时,⾄少需要x枚硬币。
def func():
coins = list(map(int,input().strip().split()))
N = int(input())
def dps(coins,N):
dpp = [N+1] * (N + 1)
dpp[0] =0
for i in range(len(dpp)):
for coin in coins:
if (i - coin) < 0:
continue
dpp[i] = min(dpp[i], 1 + dps(coins,i-coin))
return -1 if dpp[N] == N + 1 else dpp[N]
return dps(coins,N)
if __name__ == '__main__':
c = func()
print(c)
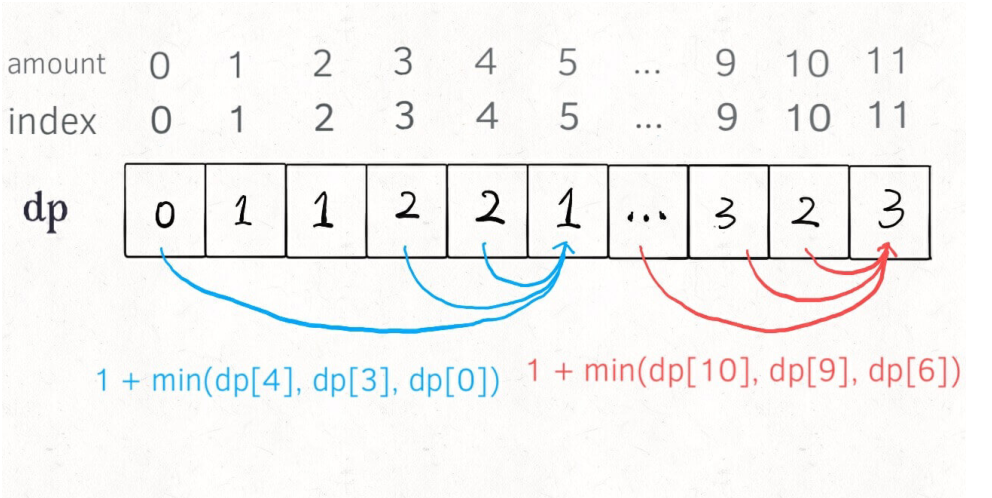
PS:为啥dp数组初始化为amount+1呢,因为凑成amount⾦额的硬币数最多只可能等于amount(全⽤1元⾯值的硬币),所以初始化为amount+1就相当于初始化为正⽆穷,便于后续取最⼩值。
最后总结
第⼀个斐波那契数列的问题,解释了如何通过「备忘录」或者「dptable」的⽅法来优化递归树,并且明确了这两种⽅法本质上是⼀样的,只是⾃顶向下和⾃底向上的不同⽽已。
第⼆个凑零钱的问题,展⽰了如何流程化确定「状态转移⽅程」,只要通过状态转移⽅程写出暴⼒递归解,剩下的也就是优化递归树,消除重叠⼦问题⽽已。
如果你不太了解动态规划,还能看到这⾥,真得给你⿎掌,相信你已经掌握了这个算法的设计技巧。
计算机解决问题其实没有任何奇技淫巧,它唯⼀的解决办法就是穷举,穷举所有可能性。算法设计⽆⾮就是先思考“如何穷举”,然后再追求“如何聪明地穷举”。
列出动态转移⽅程,就是在解决“如何穷举”的问题。之所以说它难,⼀是因为很多穷举需要递归实现,⼆是因为有的问题本⾝的解空间复杂,不那么容易穷举完整。
备忘录、DPtable就是在追求“如何聪明地穷举”。⽤空间换时间的思路,是降低时间复杂度的不⼆法门,除此之外,试问,还能玩出啥花活?