动态规划：矩阵连乘问题

一、问题描述

给定n个数字矩阵A1，A2，…，An，其中Ai与Ai+1是可乘的，设Ai是pi-1*pi矩阵, i=1,2,…,n。求矩阵连乘A1A2...An的加括号方法，使得所用的乘次数最少。

例子

• 三个矩阵连乘，可以有(A1A2)A3和A1(A2A3)两种方法求积 ，乘法次数分别为： p0p1p2+p0p2p3和p0p1p3+p1p2p3
• 假设p0=10, p1=100, p2=5, p3=50, 两种方法的次数分别是：7500 和 75000
• 明显可以看出，两种乘法在效率上是有较大差异的，计算机实现乘法比实现加法要复杂，所以如何使乘法次数最小是一个值得探究的问题

如果使用蛮力算法，对所有可能的加括号方法递归搜索，则:

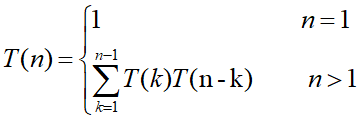
时间复杂度为指数级别，那么就需要有更优的方法来计算最佳的矩阵连乘方法

二、最优子结构性质

维基百科：如果问题的最优解所包含的子问题的解也是最优的，我们就称该问题具有最优子结构性质（即满足最优化原理）

通常来说，一个问题可以使用动态规划求解，必须具有最优子结构性质。所以，如果我们证明该问题具有最优子结构性质，我们就可以使用动态规划的方法来得到它的最优解，通常可以使用反证法进行证明。

证明：

设(A1…Ak)(Ak+1…An) 具有最少乘法次数，则(A1…Ak)中加括号的方法使A1..Ak乘法次数最少。否则设存在另一种加括号方法(A1…Ak)'更优，则(A1…Ak)'(Ak+1…An) 比 (A1…Ak)(Ak+1…An) 更优，矛盾。同理， (Ak+1…An) 内的连乘方法也是最优的。

三、实现

用m[i][j]表示Ai到Aj连乘的最小次数，则有递推关系：

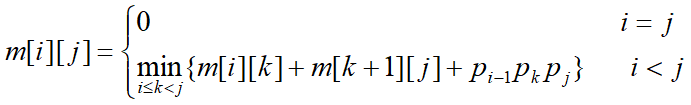
这里使用一种自底向上的动态填表的方式来进行求解。
由上式及下表可以知道，每当我们要求得一个m[i][j]的值时，都需要知道它左边位置和下边位置所有的值，这样来理解的话就很容易实现了。

i/j	1	2	3	4	5	6
1	0	0	0	0	0	0
2		0	0	0	0	0
3			0	0	0	0
4				0	0	0
5					0	0
6						0

算法过程示例

6个矩阵连乘：P=[30,35,15,5,10,20,25]

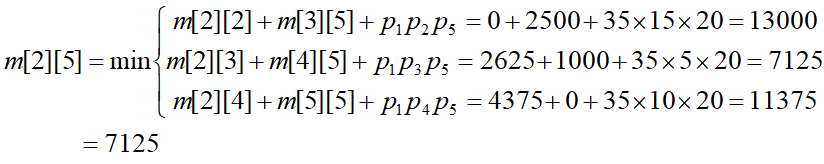
计算过程：

i/j	1	2	3	4	5	6
1	0	15750	7875	9375	11875	15125
2		0	2625	4375	7125	10500
3			0	750	2500	5375
4				0	1000	3500
5					0	5000
6						0

还可以增加一个矩阵记录分割点，求得m[i][j]值的那一个k点即为最佳分割点。
该算法的时间复杂度为

O(n^3)

代码示例

#include<iostream>
using namespace std;


//矩阵连乘问题的解
int MatrixChainOrder(int n,int p[],int a, int b){
	int m[n+1][n+1], s[n+1][n+1];//m记录乘法操作次数，s记录分割点k 
	for(int i = 1;i <= n;i++){
		m[i][i] = 0;
		s[i][i] = 0;
	}
	for(int i = n-1;i >= 1;i--){
		for(int j = i+1;j <= n;j++){
			m[i][j] = 10000000;
			for(int k = i;k <= j-1;k++){
				int sum = m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j];
				if(sum < m[i][j]){
					m[i][j] = sum;
					s[i][j] = k;
				}
			}
		}
	}
	printf("%d %d", m[a][b], s[a][b]);
}







int main(){
	int n, i, j;
	cin >> n;
	int p[n+1];
	for(int i = 0;i < n+1;i++)cin >> p[i];//第i个矩阵为pi*p(i+1)
	cin >> i >> j;
	MatrixChainOrder(n, p, i, j);
}