【题目描述】
给你一个n个点,m条边的无向图,求其生成树个数。(1<=n<=12)
【分析】
由于原问题规模较小,可以使用复杂度较高的算法,如指数级的动态规划。
那么如果n=1000呢?
【基尔霍夫矩阵】
对于无向图,它的kirchhoff矩阵定义为度数矩阵减去邻接矩阵。
在计算时,用a表示kirchhoff矩阵。则:
当i==j时,a[i][j]=i的度数。
当i!=j时,i到j有k条边相连时,a[i][j]=-k (没有边相连为0)
例如下图
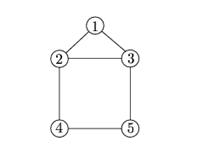
它的kirchhoff矩阵为

1 for(int i=1;i<=m;i++) 2 { 3 int x=read(),y=read(); 4 map[x][y]=map[y][x]=1; 5 } 6 for(int i=1;i<=n;i++) 7 { 8 int d=0; 9 for(int j=1;j<=n;j++) 10 if(map[i][j]) d++; 11 a[i][i]=d; 12 } 13 for(int i=1;i<=n;i++) 14 for(int j=1;j<=n;j++) 15 if(map[i][j]) a[i][j]=-1;
【Matrix-Tree定理】
对于一个无向图G,它的生成树个数等于其Kirchhoff矩阵任何一个n-1阶主子式的行列式的绝对值。
所谓n-1阶主子式,就是对于任意一个r,将C的第r行和第r列同时删去后的新矩阵,用Cr表示。
【行列式的计算】
首先有几点性质:
1、矩阵的某一行同时除以某个数,行列式的值不变。
2、矩阵的某两行相交换,行列式的值取相反数。
那么我们可以通过这些性质,把原矩阵化为三角形矩阵。则行列式的值就等于对角线上值得乘积。(从左上到右下的对角线)
1 double sum=1; 2 for(int i=1;i<=n-1;i++) 3 { 4 if(a[i][i]==0) 5 { 6 int flag=0; 7 for(int j=i+1;j<=n-1;j++) 8 if(a[j][i]!=0) 9 { 10 for(int k=i;k<=n-1;k++) swap(a[i][k],a[j][k]); 11 flag=1; break; 12 } 13 if(!flag) return 0; 14 } 15 sum*=a[i][i]; 16 for(int j=i+1;j<=n-1;j++) a[i][j]/=a[i][i]; 17 for(int j=i+1;j<=n-1;j++) 18 for(int k=i+1;k<=n-1;k++) 19 a[j][k]-=a[i][k]*a[j][i]; 20 } 21 return sum;
附spoj104代码:
就是多组数据而已。。。
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cstdlib> 5 #include<cmath> 6 #include<ctime> 7 #include<algorithm> 8 using namespace std; 9 #define MAXN 101 10 int n,m,T,map[MAXN][MAXN]; //map表示邻接矩阵,a表示基尔霍夫矩阵 11 double a[MAXN][MAXN]; 12 namespace init 13 { 14 char buf[1<<15],*fs,*ft; 15 inline char getc(){return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:*fs++;} 16 inline int read() 17 { 18 int x=0,f=1; char ch=getchar(); 19 while(!isdigit(ch)) {if(ch=='-') f=-1; ch=getchar();} 20 while(isdigit(ch)) {x=x*10+ch-'0'; ch=getchar();} 21 return x*f; 22 } 23 }using namespace init; 24 double work() 25 { 26 double sum=1; int sign=0; 27 for(int i=1;i<=n-1;i++) 28 { 29 if(a[i][i]==0) 30 { 31 int flag=0; 32 for(int j=i+1;j<=n-1;j++) 33 if(a[j][i]!=0) 34 { 35 for(int k=i;k<=n-1;k++) swap(a[i][k],a[j][k]); 36 flag=1; sign++; break; 37 } 38 if(!flag) return 0; 39 } 40 sum*=a[i][i]; 41 for(int j=i+1;j<=n-1;j++) a[i][j]/=a[i][i]; 42 for(int j=i+1;j<=n-1;j++) 43 for(int k=i+1;k<=n-1;k++) 44 a[j][k]-=a[i][k]*a[j][i]; 45 } 46 if(sign&1) sum=-sum; 47 return sum; 48 } 49 int main() 50 { 51 int T=read(); 52 while(T--) 53 { 54 memset(a,0,sizeof(a)); 55 memset(map,0,sizeof(map)); 56 n=read(); m=read(); 57 for(int i=1;i<=m;i++) 58 { 59 int x=read(),y=read(); 60 map[x][y]=map[y][x]=1; 61 } 62 for(int i=1;i<=n;i++) 63 { 64 int d=0; 65 for(int j=1;j<=n;j++) 66 if(map[i][j]) d++; 67 a[i][i]=d; 68 } 69 for(int i=1;i<=n;i++) 70 for(int j=1;j<=n;j++) 71 if(map[i][j]) a[i][j]=-1; 72 double ans=work(); 73 printf("%0.0lf ",ans); 74 } 75 return 0; 76 }