膨胀与腐蚀算法
对图像处理有所了解的人都知道图像的形态学处理里最为基础的膨胀和腐蚀算法。二值图像即只有黑白两种颜色组成的图像,一般的白色为内容,黑色为背景。其实简单点理解二值图像的膨胀与腐蚀,腐蚀即是删除对象边界某些像素,也就是让白色的区域瘦一圈;而膨胀则是给图像中的对象边界添加像素,即让白色的区域胖上一圈。而这个“圈”的大小,则是由参数来指定的。下面的表展示了一幅图像经过膨胀和腐蚀算法的结果。可以看出膨胀让白色区域大了一圈,白色区域若有较小的黑色洞,则洞被填上;而腐蚀则让白色区域瘦了一圈,一些面积很小的白色区域则消失。
 |
 |
 |
| 原图 | 腐蚀结果 | 膨胀结果 |
腐蚀膨胀的算法原理并不复杂,而且网上有太多的文章都着重于介绍算法的原理思路,对用具体代码实现算法的方式讨论的不多,因而本文专注于几种实现膨胀腐蚀算法的方法。本文介绍了几种不同的腐蚀膨胀算法的实现,每一种实现都各有特点,今后若有更多的方法,也会继续更新加入至本文中。
结构元素与窗口形态
在介绍算法逻辑之前,有必要先介绍跟腐蚀膨胀算法关系密切的结构元素。结构元素是形态学的基本算子,合理选取结构元素直接影响图像处理的效果和质量。结构元素的选择在于结构元素的形状和尺寸。结构元素可以有不同的形状,圆形、正方形、菱形、六边形、线段形都是可以选择的形状。圆形结构元素,由于各向同性,因此可以得到与方向无关的运算结果,正方形、菱形可以看作是圆盘形的变异。不同形状的结构元素运算结果会有差异,应针对待处理图像的几何形状进行选择。下表对比了正方形,圆形和正菱形三种结构元素形态。
| 预览 |  |
 |
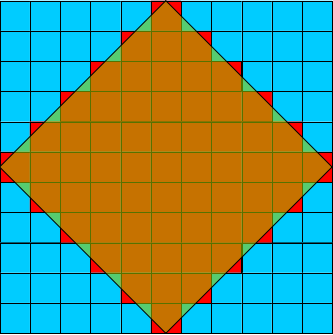 |
| ElementSize | 121 | 98 | 61 |
| WindowSize | 11×11 (r=5) | 11×11 (r=5) | 11×11 (r=5) |
| 非空点个数计算方式 | |x|<=r&&|y|<=r | x2+y2<=r2 | |x|+|y|<=r |
在算法实现过程中,往往会将卷积窗口中所有像素相对中心像素的偏移存在一个数组之中,这样在对不规则形状的卷积窗口进行处理时,可以不重复判断结构元素中哪些位置为有效位置,能减少计算次数。在实现之前首先贴上基本数据结构的实现,其中visit_count用来记录像素的访问次数:
#define byte unsigned char struct IntDouble { int X; int Y; IntDouble(int x,int y):X(x),Y(y){} IntDouble():X(0),Y(0){} }; class Bitmap2d { private: byte* data; int width; int height; public: int visit_count; Bitmap2d(int width,int height,byte v) { this->data=new byte[width*height]; memset(data,v,width*height*sizeof(byte)); this->width=width; this->height=height; this->visit_count=0; } Bitmap2d(Bitmap2d& bitmap) { this->width=bitmap.Width(); this->height=bitmap.Height(); this->data=new byte[width*height]; memcpy(this->data,bitmap.data,sizeof(byte)*Length()); this->visit_count=0; } ~Bitmap2d() { delete[] data; } inline byte GetValue(int x,int y) { visit_count++; return data[x+y*width]; } inline void SetValue(int x,int y,byte v) { visit_count++; data[x+y*width]=v; } inline int Width() { return width; } inline int Height() { return height; } inline int Length() { return width*height; } inline bool InRange(int x,int y) { return x>=0&&x<width&&y>=0&&y<height; } void ReadRaw(const char* filename) { FILE* file=fopen(filename,"rb"); fread(data,sizeof(byte),Length(),file); fclose(file); } void SaveRaw(const char* filename) { FILE *const file = fopen(filename,"wb"); fwrite(data,sizeof(byte),Length(),file); fclose(file); } };
实现思路1—根据定义直接算
首先最为简单的思路是按算法基本原理直接正向求取输出图片的像素值:
- 膨胀:对于输出图像的所有像素点P,调查原图像中对应窗口中的像素集合S,若S中至少有一个255,则P为255。
- 腐蚀:对于输出图像的所有像素点P,调查原图像中对应窗口中的像素集合S,若S中至少有一个0,则P为0。
该算法的腐蚀实现函数(膨胀的类似,就不重复贴,代码工程里有)如下:
Bitmap2d* Execute() { Bitmap2d* newBmp=new Bitmap2d(bmp.Width(),bmp.Height(),0); for(int j=0;j<bmp.Height();j++) { for(int i=0;i<bmp.Width();i++) { if(HasBlackInWindow(this->bmp,i,j)) newBmp->SetValue(i,j,0); else newBmp->SetValue(i,j,255); } } return newBmp; }
bool HasBlackInWindow(Bitmap2d& bmp,int i,int j) { for(size_t k=0;k<winOffsets.size();k++) { int tx=i+winOffsets[k].X; int ty=j+winOffsets[k].Y; if(!bmp.InRange(tx,ty)) continue; if(bmp.GetValue(tx,ty)==0) { return true; } } return false; }
膨胀腐蚀算法的主要时间开销来至于对像素的访问,从上述实现不难得该算法对于n*n的位图和k*k大小正方形结构元素访问像素的次数为k2n2。事实上这是实现腐蚀膨胀算法最直接但也是最慢的方式。下图是Engine数据的一个切片二值化之后分别用正方形、圆形和菱形为结构元素膨胀和腐蚀的效果图:
 |
 |
 |
 |
| 腐蚀(正方形) | 腐蚀(圆形) | 腐蚀(菱形) | |
 |
 |
 |
|
| 原图预览 | 膨胀(正方形) | 膨胀(圆形) | 膨胀(菱形) |
实现思路2—跳过一些内部区域
考虑到思路1的算法逻辑耗费在访问黑色区域和白色区域内部的时间较多,我们可以考虑只对黑白交界的边界考察窗口像素。这样的过程我们就可以想象成一把具有尺寸的刷子,膨胀算法刷子为白色,腐蚀算法刷子为黑色,然后让刷子在黑白交界的地方刷过,这样的过程生成的结果等价于思路1的结果。
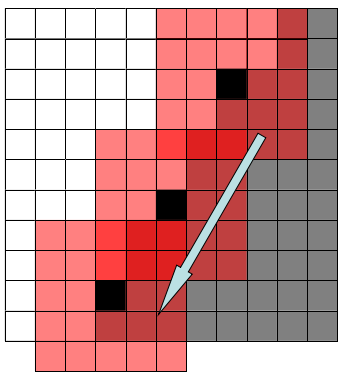
其优化的部分是针对远离边界的内部区域的涂刷,这样就能很大程度上减少像素的访问次数。不难想象出,对远离边界的内部区域的涂刷是不起效果的,这就是思路2对思路1改进的主要原因。设算法对n*n的图像按k*k的结构元素腐蚀,则访问像素的次数为a+4b1+(4+k2)b2,其中a为白色像素个数,b1为黑色内部像素个数,b2为黑色边界像素个数,且有a+b1+b2=n2。按思路2实现的算法代码如下:
Bitmap2d* Execute2() { Bitmap2d* newBmp=new Bitmap2d(bmp); for(int j=0;j<bmp.Height();j++) { for(int i=0;i<bmp.Width();i++) { if(bmp.GetValue(i,j)==0&&HasWhiteAdjacencyPixel(i,j)) { SetWindowValue(*newBmp,i,j,0); } } } return newBmp; }
bool HasWhiteAdjacencyPixel(int i,int j) { if(i>0&&bmp.GetValue(i-1,j)==255) return true; if(i<bmp.Width()-1&&bmp.GetValue(i+1,j)==255) return true; if(j>0&&bmp.GetValue(i,j-1)==255) return true; if(j<bmp.Height()-1&&bmp.GetValue(i,j+1)==255) return true; return false; }
void SetWindowValue(Bitmap2d& bmp,int i,int j,byte v) { for(size_t k=0;k<winOffsets.size();k++) { int tx=i+winOffsets[k].X; int ty=j+winOffsets[k].Y; if(!bmp.InRange(tx,ty)) continue; bmp.SetValue(tx,ty,v); } }
基于结构元素分解的算法
对于一些具有规则形状的结构元素,可以利用矩阵分解的原理降低计算次数,例如3*3的正方形结构元素,等价于一个3*3的矩阵,这个矩阵可以为解为{1,1,1}与{1,1,1}-1的乘积。这样使用3*3的矩阵对图像进行卷积等价于先使用{1,1,1}进行卷积,再将结果使用{1,1,1}-1进行卷积。

由于膨胀腐蚀算法本质上属于卷积的一种特殊形式,这样,正方形结构元素的膨胀腐蚀可以使用如下的方式实现:
Bitmap2d* Execute4() { Bitmap2d* newBmp=new Bitmap2d(bmp); Bitmap2d* newBmp2=new Bitmap2d(bmp); if(this->mode==SQUARE) { winOffsets.clear(); for (int i = 0; i < 2 * radius + 1; i++) { IntDouble t(i-radius,0); this->winOffsets.push_back(t); } for(int j=0;j<bmp.Height();j++) { for(int i=0;i<bmp.Width();i++) { if(HasBlackInWindow(this->bmp,i,j)) newBmp->SetValue(i,j,0); else newBmp->SetValue(i,j,255); } } winOffsets.clear(); for (int j = 0; j < 2 * radius + 1; j++) { IntDouble t(0,j-radius); this->winOffsets.push_back(t); } for(int j=0;j<newBmp->Height();j++) { for(int i=0;i<newBmp->Width();i++) { if(HasBlackInWindow(*newBmp,i,j)) newBmp2->SetValue(i,j,0); else newBmp2->SetValue(i,j,255); } } } newBmp2->visit_count+=newBmp->visit_count; delete newBmp; return newBmp2; }
经过测试可以知道这种方式可以大大减少像素访问次数,以k*k的结构元素腐蚀n*n的图像为例,用思路1的方法需要至少访问k2n2次像素,经过分解再处理两次只需要2kn2次访问。这个思路的详细数学原理可以参考链接。
下图是分解的方法与思路1的方法的结果对比,可以看出这两个算法的结果确实是完全等价的。
 |
 |
| 思路1 | 分解的方法 |
基于曼哈顿距离的算法
上述思路1思路2可以适用于任意形状的处理窗口。还有一种基于曼哈顿距离的实现方式,来源于链接,这种方式主要是实现了基于菱形窗口的膨胀腐蚀。这里简单介绍一下曼哈顿距离,曼哈顿距离(Manhattan Distance)是种使用在几何度量空间的几何学用语,用以标明两个点在标准坐标系上的绝对轴距总和。其计算公式为:
![]()
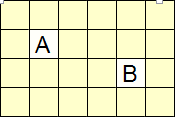
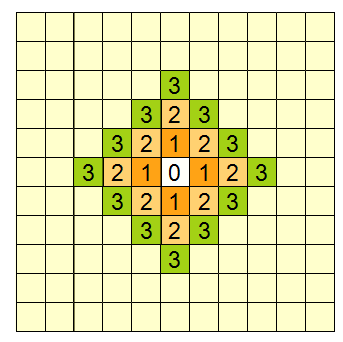
这个距离简单点理解就是“格子距离”,如下图所示:A到B的走格子的最少步数是4,那么AB的曼哈顿距离就是4。
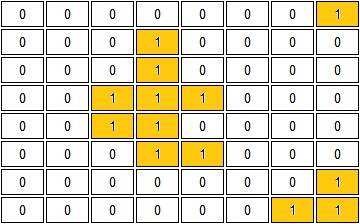
设我们需要膨胀的图像是下图左这样一个背景为0,内容为1的二值图像。假如我们能够求得所有0像素到离自己最近的1像素的距离的话,我们便做成了一张曼哈顿距离图(下图右)。曼哈顿距离图中像素标的数字代表该像素在左图中寻找最近的1的曼哈顿距离。假如这个像素在左图中本来就是1,则该像素处的曼哈顿距离为0。可以看出,01边界处的0像素的曼哈顿距离较小,而原理边界的0像素曼哈顿距离很大。
 |
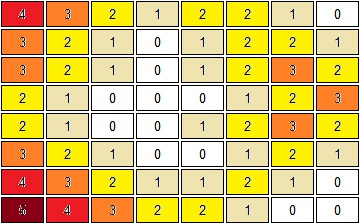 |
| 原图 | 原图得到的曼哈顿距离图 |
对于二值图像I,若能够一定处理计算得到他的曼哈顿距离图D,则想求取他的菱形结构元素膨胀结果会非常容易。不难想到,对D进行一个阈值化既可以达到结果。若将曼哈顿图D中曼哈顿距离大于等于1与小于1的像素区分开,则等于原二值图像;若将曼哈顿距离大于等于2与小于2的像素区分开,则等价于对原二值图像进行一个尺寸为1的菱形元素膨胀;若将曼哈顿距离大于等于k(k>1)与小于k的像素区分开,则等价于对原二值图像进行一个尺寸为k的菱形元素膨胀。
而腐蚀同样可以使用这个思路来完成,前面介绍的曼哈顿距离图是适用与膨胀的,求取的是每个0像素与距离最近的1的距离。在腐蚀的场合下,我们可以求取所有1像素与距离最近的0像素距离的曼哈顿图,这样再进行阈值化,也就完成了腐蚀操作。利用曼哈顿图的好处还体现在需要使用对很多组不同大小的结构元素对相同图像进行膨胀或腐蚀的场合。一旦计算出曼哈顿距离图,就可“一次预处理,多次复用”,预处理的开销只在初次处理产生,之后的所有操作都是阈值化的过程,而阈值化我们知道只需要width*height的访问开销。
所以问题的关键在与如何实现对二值图像I求取其曼哈顿距离图D。这里以求取膨胀的曼哈顿距离图为例进行说明。其实我们可以利用一种类似于动态规划的思想来解决这个问题。不难发现这个问题是能够分解为规模更小并且可以复用的小型子问题的和。这基于如下的事实:
- 对于所有I中为1的像素,D中他们为0。因为他们自己就是1像素显然到自己最近,所以不需要走格子。
- 对于I中的0像素p,若其四邻域像素在D中为d0、d1、d2、d3,则D(p)=min(d0,d1,d2,d3)+1。不难看出p到离其最近的1像素的通路必然经过了其四邻域像素。所以0像素p到最近的1的像素的曼哈顿距离可以基于其四邻域的曼哈顿距离求得。
要实现这个思路,可以使用递归,但也可以使用更加直接的方式,下面的代码使用两次双循环来求得D。首先每个像素d值默认值为最大值width+height,第一次双循环,对每一个像素实际上是考察了上方和左方的像素,经过这一次循环,其d值不一定正确,仅是能够保证每个像素处的d值是相对与上方和左方的最小值加1;但第二次双循环是逆向,从下方和右方访问像素,依次再改变之前的d值,这样就实现了d值确实为min(d0,d1,d2,d3)+1。
 |
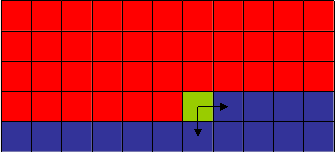 |
| 行序正向赋值,每个像素参考了两个父方向的d值 | 第二次迭代行序逆向复制,每个像素参考4个方向的d值 |
采用这个思路实现的一个演示程序如下(不能跑刷新几次试试..):
其实现的代码如下:
class DistenceMap { private: int* data; int width; int height; public: int visit_count; DistenceMap(int width,int height,int v) { this->data=new int[width*height]; for(int i=0;i<width*height;i++) data[i]=v; this->width=width; this->height=height; this->visit_count=0; } ~DistenceMap() { delete[] data; } inline int GetValue(int x,int y) { visit_count++; return data[x+y*width]; } inline void SetValue(int x,int y,int v) { visit_count++; data[x+y*width]=v; } inline int Width() { return width; } inline int Height() { return height; } inline int Length() { return width*height; } };
Bitmap2d* Execute3() { Bitmap2d* newBmp=new Bitmap2d(bmp); DistenceMap* dmap=GetDistenceMap(); for (int i=0; i<bmp.Width(); i++) { for (int j=0; j<bmp.Height(); j++) { byte v=dmap->GetValue(i,j)<=radius?0:255; newBmp->SetValue(i,j,v); } } newBmp->visit_count+=dmap->visit_count; delete dmap; return newBmp; }
DistenceMap* GetDistenceMap() { DistenceMap* distenceMap=new DistenceMap(this->bmp.Width(),this->bmp.Height(),0); for (int i=0; i<bmp.Width(); i++) { for (int j=0; j<bmp.Height(); j++) { if (bmp.GetValue(i, j) == 0) { distenceMap->SetValue(i,j,0); } else { distenceMap->SetValue(i,j, bmp.Width()+bmp.Height()); if (i>0) distenceMap->SetValue(i,j,Min(distenceMap->GetValue(i,j),distenceMap->GetValue(i-1,j)+1)); if (j>0) distenceMap->SetValue(i,j,Min(distenceMap->GetValue(i,j), distenceMap->GetValue(i,j-1)+1)); } } } for (int i=bmp.Width()-1; i>=0; i--) { for (int j=bmp.Height()-1; j>=0; j--) { if (i+1<bmp.Width()) distenceMap->SetValue(i,j,Min(distenceMap->GetValue(i,j), distenceMap->GetValue(i+1,j)+1)); if (j+1<bmp.Height()) distenceMap->SetValue(i,j,Min(distenceMap->GetValue(i,j), distenceMap->GetValue(i,j+1)+1)); } } return distenceMap; }
总结
本文介绍的实现方式,思路1和思路2是基本方法,其中思路2是对思路1的极大改进;矩阵分解方法适用于一些特殊形状的结构元素,其核心是把结构元素所代表的矩阵分解成两个更简单的矩阵的乘积,然后再使用这两个更简单的矩阵作为结构元素。这个思路同样能与思路1和2相配合使用;曼哈顿距离法使用一步预处理先计算出曼哈顿距离图,之后再对这个图进行阈值化,等价于使用菱形结构元素进行的膨胀腐蚀的结果,对于需要多次膨胀腐蚀的场合,这个方法非常适用。
目前先介绍这么多,日后再有好的实现方法,会对本文进行补充。代码工程下载:https://github.com/chnhideyoshi/SeededGrow2d/tree/master/DilateErodeImp
爬网的太疯狂了,转载本文要注明出处啊:http://www.cnblogs.com/chnhideyoshi/