红黑树的概念,这里不做阐述。网上一抓一大把。本文仅以个人的理解介绍一下红黑树自平衡的过程。
红黑树的性质:
- 性质1:每个节点要么是黑色,要么是红色。
- 性质2:根节点是黑色。
- 性质3:每个叶子节点(NIL)是黑色。
- 性质4:每个红色结点的两个子结点一定都是黑色。
- 性质5:任意一结点到每个叶子结点的路径都包含数量相同的黑
自平衡所需要的操作,无非是变色,左旋,右旋。变色不用多说,黑变红红变黑。关于左旋,先附上网上找到的一个图
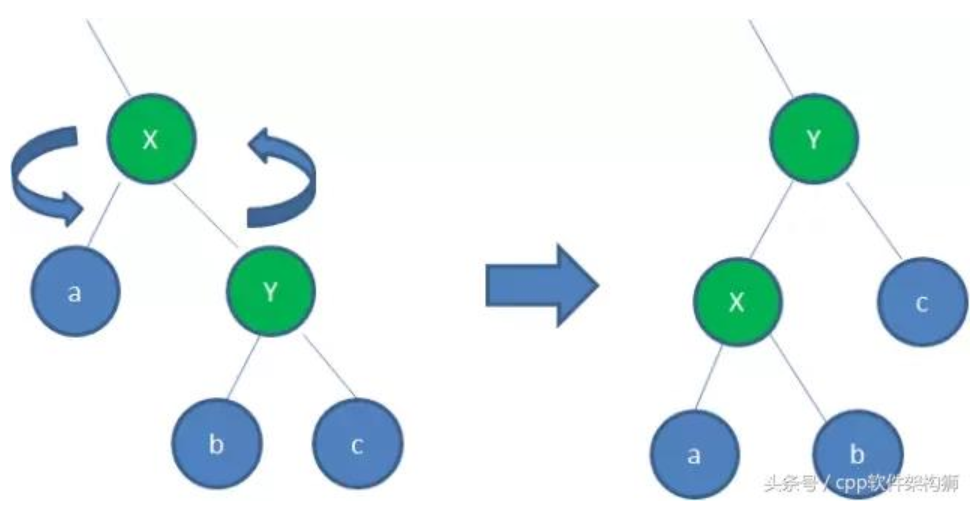
图片来源:http://www.360doc.com/content/18/0904/19/25944647_783893127.shtml
由于红黑树本身是一棵二叉搜索树,即左子树的所有节点值都小于自己,右子树的所有节点值都大于自己。于是,在旋转过程,把y提为本子树的根节点时,由于y原来是x的右孩子,y > x,x成为y的左孩子。y原本的左孩子b就得给x腾出位置,x的右节点恰好空了出来。b原为x的右子树成员,b > x,成为x的右孩子很合理。
关于右旋,原理相同。

图片来源:http://www.360doc.com/content/18/0904/19/25944647_783893127.shtml
现在开始说明红黑树的自平衡。
首先是插入节点的着色。所有关于红黑树自平衡的介绍都说,插入的节点为红色。至于为什么,笔者认为,由于性质3与性质5,任意一结点到每个叶子结点的路径都包含数量相同的黑,且每个叶子节点(NIL)是黑色。新插入的节点初始位置必为替换某个叶子节点,同时自己又会新产生左右两个叶子节点。若新插入的节点为黑,则将会引起从根节点到新节点的路径上黑色节点数量比其它路径多了1。而插入红色节点,则不会有此情况,但是有可能会违反性质4,每个红色结点的两个子结点一定都是黑色,出现连续的两个红色节点,但是不是必然发生。所以新插入的节点为红色,可以使得需要自平衡操作的几率降低。
然后,若真的出现了连续两个红色节点的情况,不影响整体黑高的情况下的调整,能大大降低调整次数。
在新插入一个红节点时,除了当前是空树外可能的情况有:
1、其父节点为黑色。这种情况不会改变其父节点处的黑高,也不会打破任何性质。不用做任何处理
2、其父亲节点为红色。由于红黑树是自平衡的,在新插入一个节点之前,它已经是平衡的,满足所有性质。故其祖父节点一定为黑色。
a.其叔叔节点为叶子节点。若为在根节点的右孩子的左子树上插入新节点(RL)。单纯修改其父节点颜色并不能使其平衡。

若直接对20,10进行左旋,则得到
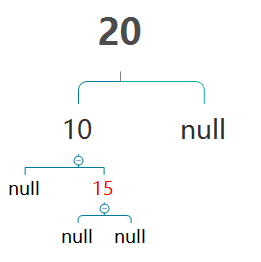
又用相同方式左旋,将又会得到初始状态,死循环。若先对15,20进行右旋,则将会得到RR:
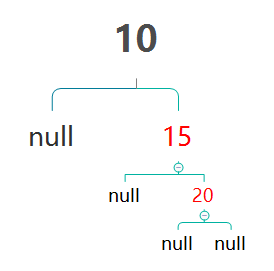
此时再对10,15进行左旋,将会得到:
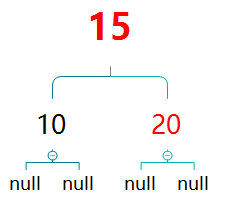
然后再对10,15进行变色
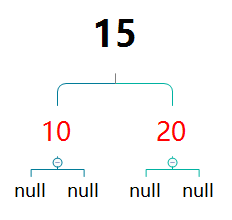
此时达到平衡。LR的情况与之相同,操作方式相反,不再单独叙述。而RR的情况上面已经描述,LL与RR情况相同,操作相同,亦不做描述。
b.其叔叔节点为红节点

此时直接同时把父节点与叔叔节点进行变色
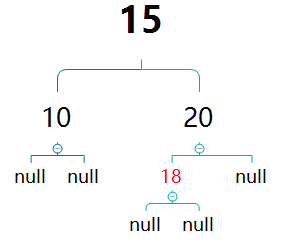
而此时将会导致祖父节点15的黑高+1。因不确定其是否还有父节点,为了不必要的麻烦,将15设置为红色,即可保持15的黑高不变。

说明:此处仅以15做为某树的子树的根节点,并非打破性质2。
c.其叔叔节点为黑色节点(非叶子)此情况在刚插入时并不存在。理由如下:每条路径的黑色节点数量必须相同。若新插入的节点的父节点是红色,而叔叔节点是黑色,则只能说明叔叔节点的黑高比父节点的多1。
现以一个简单的实例:
向一棵红黑树顺序插入数字1,2,3,4,5
首先,插入1,红节点。
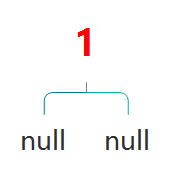
根据性质2,根节点是黑色,直接换成黑色即可。此时黑高为2
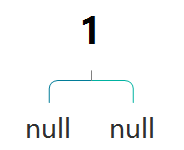
然后插入2。并未打破5大性质,不用做任何处理。此时所有路径的黑高为2。
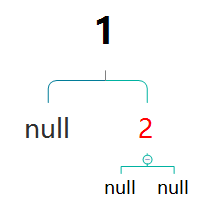
插入3之后(RR)
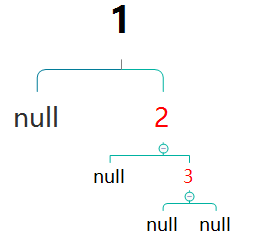
对3的父亲节点2与祖父节点进行左旋,然后变色
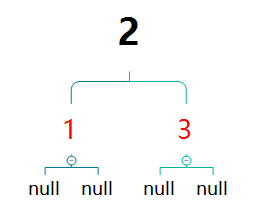
然后继续插入4
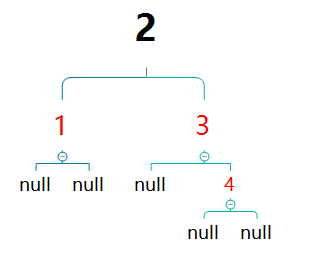
此时再次出现相邻红色节点。4的父亲节点3与叔叔节点1均为红色,此时将二者都进行变色操作,一可保持性质4,二不会改变黑色节点之差。
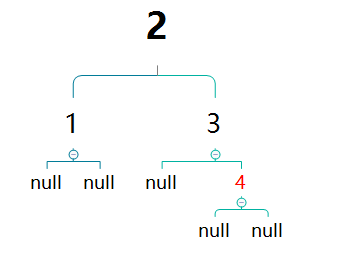
此操作之后,4的祖父节点2的黑高+1。若其为某红黑树的某子树,则会破坏平衡。故将其进行变色处理。
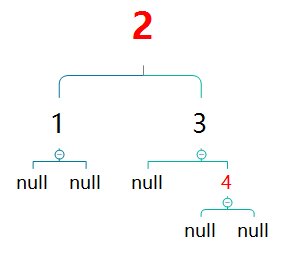
然后继续以2为基础做自平衡。发现其已经是根节点,没有父节点,自己的子树已达到平衡,不用继续处理。然后根据性质2,将其设置为黑色。此时黑高为3。
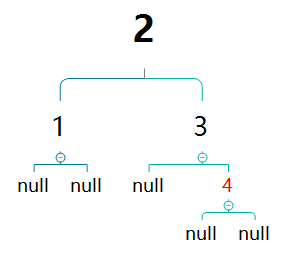
继续插入5
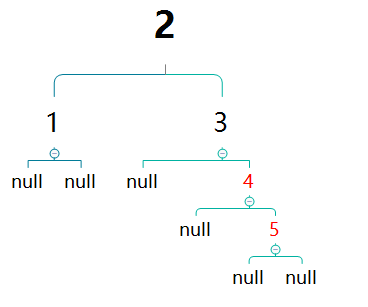
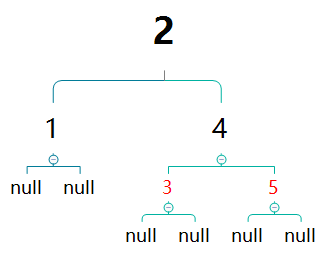
再次出现相邻红色节点,情况与插入3时相同,做相同处理
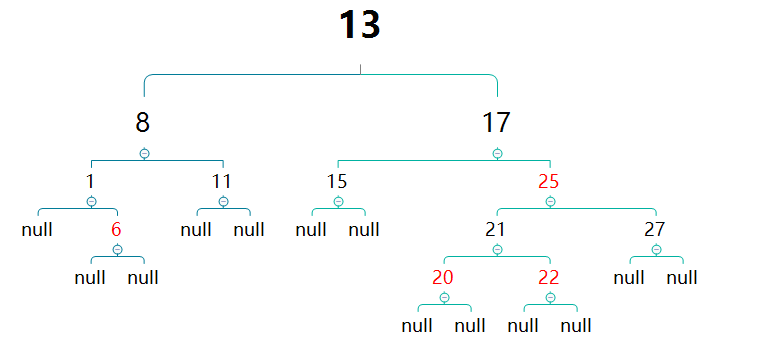
现分析下列红黑树插入节点21的情况。插入之前,根节点的黑高为3。

图片来源:http://www.360doc.com/content/18/0904/19/25944647_783893127.shtml
说明:前几步与来源讲解的有点类似,最后并不像来源处将13 17左旋了。

节点21 22为相邻红色节点,要对新插入的节点21的父节点22进行变色。21的叔叔节点27同为红色,与22同时变色,可保证21的祖父节点25保持平衡。
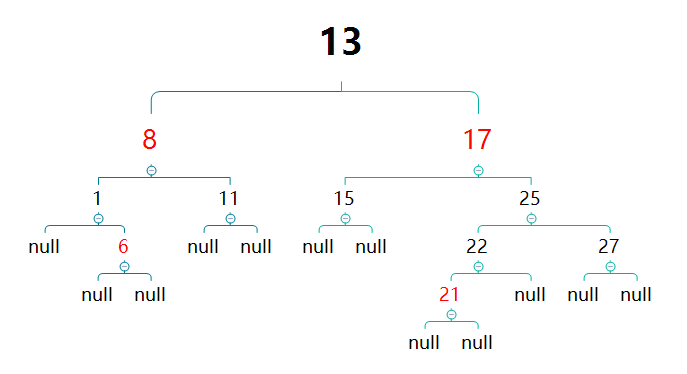
而此操作之后,将会导致25子树黑高+1,使得其黑高比其兄弟节点多1。为了防止这种情况,25需要跟着色,才能保证25节点子树的黑高不变,从而不影响整个红黑树的黑高。

虽然整体黑高没有发生变化,但是再次出现了相邻红色节点17 25。用相同策略,把8,17,13同时进行变色。

此时13节点的左右子树的黑高均是3,保持平衡。且13为根节点,没有父节点,13的平衡代表整个红黑树的平衡,不用再继续处理。 然后根据性质2,将根节点13改为黑色。

若此时再插入节点20,则

由于20的叔叔节点为黑色节点,单纯修改父节点为黑色,只会导致祖父节点变得不平衡。旋转21,22,并各自变色,就可以达成平衡