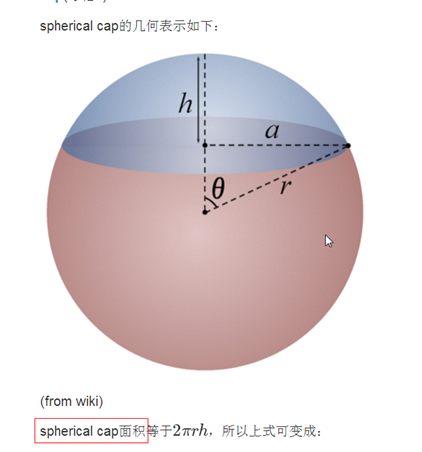
电磁场电磁波 书上的教材p32面
引入立体角是为了证明高斯定理。
我曾经学习过的高斯定理证明方法是在场论初步里面证明的
在证明这个定理之前,首先要明确:
- 场的强度表达式决定了该散度div是否为0,div为0就是保守场。
- 从测度的角度看,去掉定义域里面有限个不连续的点,积分值不变
- 真空中点电荷场强公式
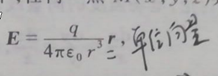
- 点电荷散度公式
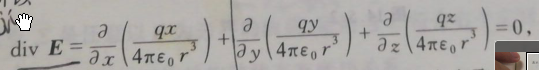
我们分类讨论
- 点电荷位于圆心,曲面Ω是一个原点位于圆心,半径为R的球面,所以

- 设Ω是光滑闭曲面,
A.如果Ω不包含原点,由高斯公式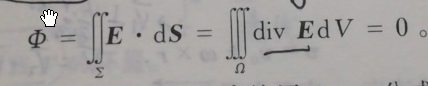
B.如果Ω包含原点,取一个小球面Σ包含住这个原点,记Ω1为Ω和Σ之间的区域。
由高斯公式得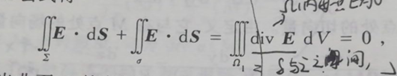
(因为没有原点用A)
所以通过Ω1的通量是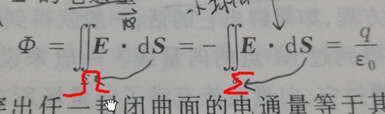
Σ是小球面,用情况1
得证
详细的说明,还需要用到曲面的侧,散度div与通量之间的关系,我觉得很麻烦,就不说了
下面解释为什么对于闭合曲面立体角是0?
预备知识
立体角是单位球面上的一块面积
教材P32一开始并没有给出立体角的定义,只是对规则的球面和不规则的封闭曲面给出计算的公式。
他的解释方法和证明高斯定理完全一致,可是他却始终没有给出立体角的定义。让读者无法解释为什么当点p在不规则曲面外时,无法理解他到底是如何抵消的?我一开始是考虑通量与书上不规则立体角计算公式得关系,可是通量不会有除以半径的平方。于是我果断放弃这种想法。
然后百度一搜,立体角的定义,很自然的解释了为什么抵消? 其实因为当你的射线,从封闭曲线的一端穿出封闭曲线的另外一端,你的张开的角度是相同的。曲面的法向量是相反的。 法向量相反,投影到单位球面的面积绝对值相同但是符号相反。立体角自然就抵消为0
再给出,另外一种球面对球心立体角为4Pi的解释,虽然计算起来比书上复杂,但是理解起来却更加轻松。