序言
这篇笔记是阅读《基于OMAP-L138的异步电动机轴承故障检测系统研究》后写的笔记。
轴承故障约占电机故障的30%-40%，滚动轴承的损伤形式主要有：疲劳脱落，磨损，腐蚀，胶合，塑性变形，断裂，保持架损坏。因此对轴承故障的分析很重要，笔记从5个方面来叙述我的所感所得。
- 轴承故障的三种检测方式；
- 故障信号处理方法；
- 滚动轴承故障的定子电流频谱特征；
- 自适应滤波及连续细化傅里叶变换结合的方法；
- 基于SVD和ADES算法的轴承故障诊断方法。
一：轴承故障的三种检测方式
- 温度分析法：对轴承载荷，转速，润滑的变化比较敏感，对轴承润滑不良导致的过热的情况尤其敏感。但是只有当故障恶化到一定程度时才会起作用，并且不适合腐蚀，疲劳脱落等局部伤类故障。
- 振动分析法：安装振动传感器，采集轴承振动始于信号，变换频域进行频谱分析，最后再通过对比判断故障。当轴承故障振动信号频谱包括特征频率，通过特征频率的识别来判断轴承是否出现故障。
- 定子电流信号分析法：对一相定子电流信号进行频谱分析，通过与正常定子电流信号频谱对比判断故障。缺点是容易受背景噪音，负荷波动等因素的干扰。
二：故障信号处理方法
- 快速傅里叶变换：默认具备一些复数相关知识（不具备也没关系）
傅里叶变换（https://www.cnblogs.com/h2zZhou/p/8405717.html）
FFT链接(https://blog.csdn.net/enjoy_pascal/article/details/81478582)
傅里叶变换是将原来难以处理的时域信号转换为易处理的频域信号（信号的频谱）。但计算机处理信号要求时域和频域均是的是离散，有限长的，由此便产生了离散傅里叶变换，而快速傅里叶变换便是对离散傅里叶变换的一种优化，减少了其计算复杂度，大大提升了离散傅里叶变换的运算效率。
输入信号是$x(t)$，经过Hilbert变换的结果是
其基本思想是通过对基波分量（工频正弦波）的消除来实现对异步电动机故障特征的提取。采取的方法是将交流基信号转为直流分量，消除了基波对故障信号的影响，方便了故障信号的提取。
小波变化是弥补傅里叶变换局部变换能力的不足，第一个原因是傅里叶变换是整体特征，没有局部特征。如果信号在时域上发生了突变，那么需要大量的三角函数在频域上进行拟合。第二个原因是对于非平稳信号，傅里叶变换只能看到由哪些频域组成，无法看到突变频域发生的时刻，所以可能发生在时域上相差很大的信号，其频谱图可能一致，例如下图：
为了解决这种问题，小波变换将傅里叶变换的基底更换了——从无限长的三角函数基换成了有限长的会衰减的小波基。这样不仅能够获取频率，还可以定位到时间了（开森不~~）
其中a对应频率，控制伸缩，t对应时间，控制平移，由此可见小波分析很适合非平稳信号的局部特征分析。
- Hilbert-Huang变换：（https://blog.csdn.net/lvsehaiyang1993/article/details/80875679)
Hilbert变换要求信号只能是线性稳态的，而实际中的信号大多并不是如此，为了解决这个问题提出了 希尔伯特-Huang变换。其思路是下列三个步骤：
- 输入原始信号
- 经过Huang的算法（经验模式分解（EMD），固有模态函数（IMFs））
- Hilbert谱分析。
其中Huang的算法步骤如下图所示：
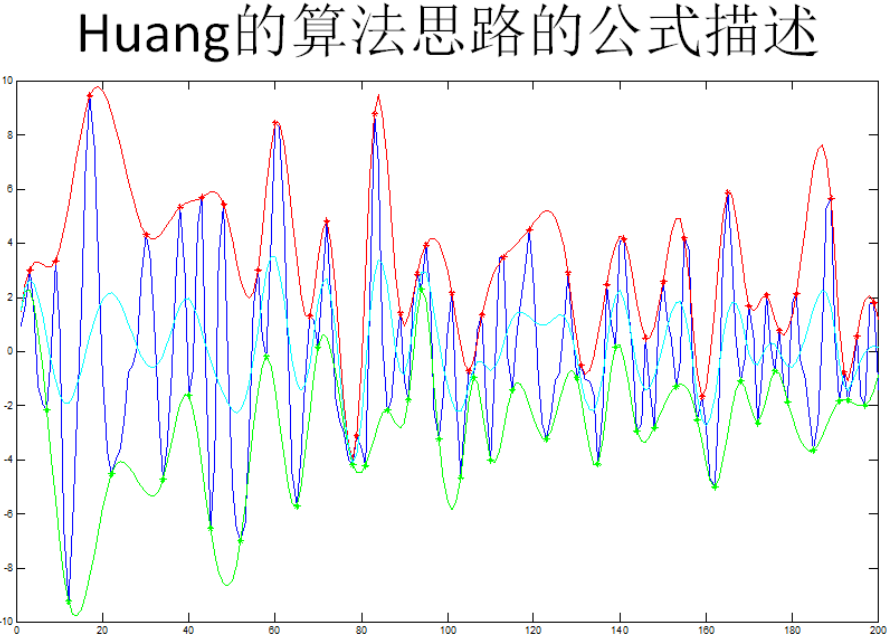运用流程图来表示是如下步骤：
HHT具有很强的自适应性，能够随着处理信号的变化而将分解过程进行调整，对处理非平稳信号也具有很好的效果。
三：滚动轴承故障的定子电流频谱特征
滚动轴承故障主要分为3类，外圈故障，内圈故障和保持架故障，轴承出现故障可用振动和电流信号来分析，电流分析原理步骤如下图所示：
- 外圈故障，内圈故障和保持架故障；
- 相应的电动机转轴振动；
- 电动机內膛气隙振动；
- 气隙磁通受到调制；
- 调制的磁通又在定子绕组中感生出相应的谐波电流
异常原因和相应的公式如下表所示：
| 异常原因 | 振动频率特征 | 电流信号特征频率 |
| 外圈损伤 | $Zf_{oc}$ | $|f_{s}pm k Zf_{oc}|$ |
| 内圈损伤 | $Zf_{ic}$ | $|f_{s}pm k Zf_{ic}|$ |
| 保持架损伤 | $Zf_{bc}$ | $|f_{s}pm k Zf_{bc}|$ |
四：自适应滤波及连续细化傅里叶变换结合的方法
x(n)表示输入电流信号，y(n)表示输出信号，e(n)表示误差信号，d(n)表示想要滤除的贡品信号和各次谐波分量的参考信号，通过自适应算法确定自适应滤波系数的迭代方式，从而使e(n)= d(t) - y(t) = d(t) - W/X(t)最小，常用的迭代系数的算法是最小均方算法（LMS），大概思路如下所示：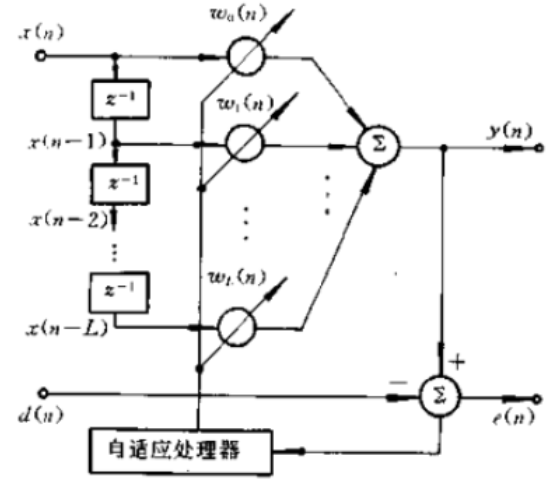
自适应滤波的目的是为了滤除定子电流信号中的工频分量以及谐波分量（电流中含有的频率为基波整数倍的电量，产生原因是由于正弦电压施加于非线性负载时，基波发生变化产生谐波）。以突出故障特征频率分量。
- 连续细化傅里叶变换
FFT使用时有一定的局限性，设采样频率为fs，采样点数为N，采样周期为Ts，频率分辨率（频率间隔）为f_div = fs / N，又因为采样时间是Ts = N / fs，因此有
f_div = 1 / Ts
也就是说频率间隔越小，那么对应的频谱上的线就越多，频率分辨率就越高。若想提高频率分辨率又不想降低采样频率，那就只能增加采样时长。这也就意味着运算速率和分析速率会降低。
连续细化傅里叶变换是对它的优化，指应用连续的傅里叶变换频域曲线，对FFT谱在指定区域内，特别是一个频率间隔内，进行指定密度的细化。即它可以有效估计信号中某一频率分量，应用于电机故障检测时，可以估计工频分量，主要的谐波分量。因此可以通过连续细化傅里叶变换构造基波电流，三次、五次谐波电流信号。将其当作噪声信号通过自适应滤波滤除，同时可以估计故障频率信号。
- 自适应滤波与连续细化傅里叶变换结合的新方法
- 采集定子电流瞬时信号
- 通过小波分解，得到不同频率范围的分解信号
- 对分解信号进行连续细化傅里叶变换，形成噪声信号
- 通过自适应滤波滤除噪声
- 通过连续傅里叶变换进行频谱分析。
五：基于SVD和ADES算法的轴承故障诊断方法
博客园敲矩阵太麻烦了，放弃了，直接上图（溜了溜了~~~~）
其中Hankel矩阵为每一条逆对角线上的元素都相等的矩阵，举例：
奇异值反映的是采集信号的各个频率分量，大奇异值对应大能量频率分量，包括工频分量，低次谐波分量，故障特征频率分量等。小奇异值对应低能量频率分量，包括背景噪声，保留前K个较大的奇异值，其余置0，重构hankel矩阵，R(K)，用R - R(k)的F范数来表示逼近质量。
定义归一化比值：
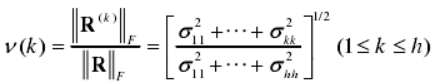
SVD滤波的效果取决于K的取值，可采用两种方法来决定，第一种是预先设定归一化比值的大小，第二种是根据采样信号的频率组成以及要提取的频率分量来确定。k没有定值，应根据滤波效果以及滤波目标灵活选择。
SVD算法步骤如下：
注意事项：对于故障分量而言，工频能量大而且集中，故对应数值较大的奇异值，为了消除工频分量的影响需进行两次SVD滤波，第一次是滤除工频分量，第二次是滤除噪声分量。
- APES算法
APES滤波器用于信号幅值和相位估计。
目的是使得频率为wk的信号无失真地通过滤波器，同时尽可能抑制信号X(n)中的其他频率分量和噪声，w为滤波器权向量，因此有wkTa(w) = 1，通过计算可将上述问题转换成约束优化问题：
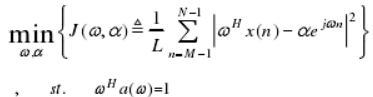
APES适合用于短时信号，对短时信号有较高分辨力，可以有效估计故障特征频率。
- SVD和APES相结合的算法流程
- 采集信号x(n)
- 构造Hankel矩阵
- 一级SVD滤波
- 二级SVD滤波
- APES频率估计。
感悟
既然是随笔，在最后就写点自己的感想吧，故障检测大概可以分为两部分，一部分是将原始信号处理成可分析的信号，另一部分是分析处理好的信号，进而得到故障信号的频率。这还只是原理和公式部分，程序部分还没有看。内容多多哒，问题也多多哒，看来还有好长的路要走哇~~~顺便吐槽一下，博客园的公式编辑真的好麻烦啊啊啊啊啊，还各种出问题（哭唧唧~~~）