出发点:
线性判别函数在进行分类决策时是最简单有效的,但在实际应用中,常常会出现不能用线性判别函数直接进行分类的情况。 采用广义线性判别函数的概念,可以通过增加维数来得到线性判别,但维数的大量增加会使在低维空间里在解析和计算上行得通的方法在高维空间遇到困难,增加计算的复杂性。 引入分段线性判别函数的判别过程,它比一般的线性判别函数的错误率小,但又比非线性判别函数简单。
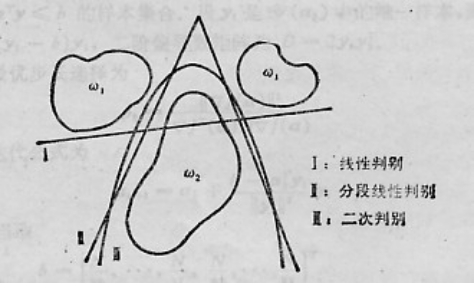
图例:
用判别函数分类 可用一个二次判别函数来分类 也可用一个分段线性判别函数来逼近这个二次曲线
分段线性判别函数的设计
(1)采用最小距离分类的方法

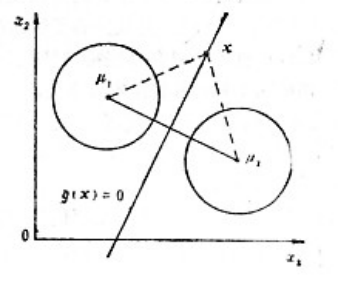
图例:分段线性分类设计

3.4 模式空间和权空间


模式空间 :
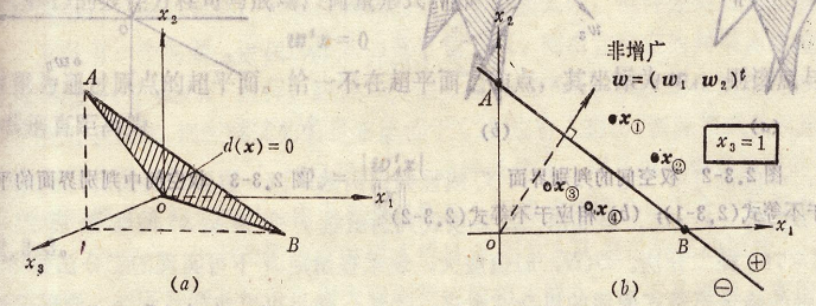
对一个线性方程w1x1+w2x2+w3x3=0,它在三维空间(x1 x2 x3)中是一个平面方程式,w=(w1 w2 w3)T是方程的系数。 把w向量作为该平面的法线向量,则该线性方程决定的平面通过原点且与w垂直。若x是二维的增广向量,此时x3=1,则在非增广的模式空间中即为{x1, x2 }二维坐标,判别函数是下列联立方程的解

(a)增广向量决定的平面 (b)非增广向量决定的直线
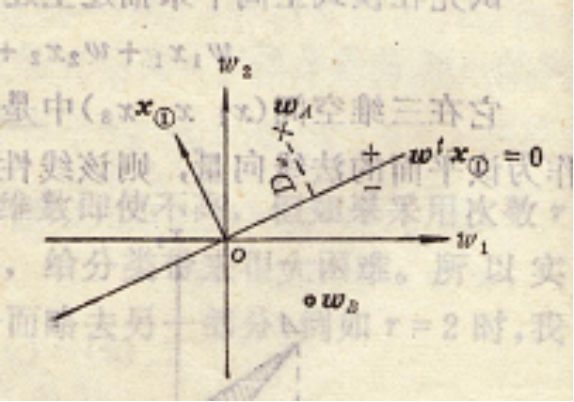
权空间:
若将方程x1w1+x2w2+w3=0绘在权向量w=(w1 w2 w3)T的三维空间中,则x=(x1 x2 1)T为方程的系数。 若以x向量作为法线向量,则该线性方程所决定的平面为通过原点且与法线向量垂直的平面,它同样将权空间划分为正、负两边。 在系数x不变的条件下,若w值落在法线向量离开平面的一边,则wTx>0,若w值落在法线向量射向平面的一边,则wTx <0。
权空间中判别界面的平面示意图