参考资料:
https://inst.eecs.berkeley.edu/
USTC_MIRA_ML_Slides Lecturer: Jie Wang
机器学习课上到了增强学习这一节,其中提到了Markov决策过程以及增强学习的一些个算法(比如:增强学习中的Q-learning算法,MDP中的value-iteration和policy-iteration)。但是其中还有一些不太明白的地方,查找资料的时候发现了加州大学伯克利分校的AI课件。阅读之后豁然开朗,下面是我学习了MDP之后的一点自己的理解,会多讲自己感觉难的地方,省略容易的地方,也不会有证明,但会有思路。(插句题外话:阅读了伯克利的slides之后觉得这些世界顶尖的大学为全球的教育做出了不可磨灭的贡献,假如学不好英语,科研工作很难开展。)
Markov过程大家都很熟悉,最大的性质就是无后效性。MDP就是在一个马尔科夫过程中找到我们眼中的“最优”策略。下面给出一些基本的定义:
有了这些定义,我们就可以定义我们眼中的“最优”:即累计reward最大!这个累计reward被记作$V(s)$,即每个状态的累计reward,下面给出$V(s)$的定义!!这里千万要注意是定义,是我们最本原的东西--即累计reward~
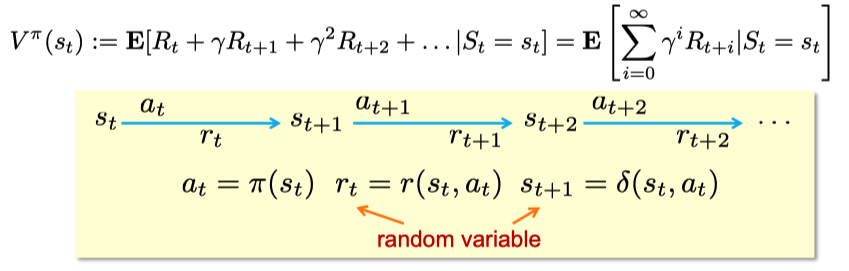
上面的$V$有一个头标$pi$,这个$pi$就是所谓的policy即策略。$r(s,a)$是我们的单步reward,在stochasitc(非deterministic)的环境中,它是一个随机变量。所以$V^pi(s)$就是从状态$s$出发,遵循策略$pi$我们获得的累计reward. 然后我们定义了一个所谓的$Q-function$,这个$Q-function$是什么呢,$Q^pi(s,a)$就是在当前状态为$s$的情况下采取行动$a$获得一个单步reward,再加上状态$s'$的累计reward,即$Q^pi(s,a)=E[r(s,a)]+gamma sum_{s'}[mathbf{P}(s'|s,a)V^pi(s')]$。这里的$gammain[0,1)$是一个discount,discount的存在方便了我们之后所有的公式推导,和收敛性有密切关系。
从上面的定义我们可以自然导出贝尔曼方程(Bellman Equation):
$$V^pi(s)=mathbf{E}[r(s,pi(s))]+gammasum_{s'}mathbf{P}(s'|s,pi(s))V^pi(s')$$
矩阵化:
$$V=(I-gamma T)^{-1}R$$
其中reward向量$R$和转移矩阵$T$取决于policy(矩阵化了所以每个s都考虑到了),由此可见$V$这个东东,也就是当前策略下的Value-function取决于policy $pi$ (不妨把$pi$想象成Value-function的参数)。由于$gammain[0,1)$,我们可以证明$I-gamma T$是可逆的,证明方法是利用$T$是一个转移概率矩阵,也是一个stochastic matrix,有极大特征值1,以及利用可逆矩阵的齐次方程仅有零解来证明。由此 Bellman's equation admits a unique solution!
好了,上面定义了一大堆东西,我们回归本心,要干什么?答:极大化$V^pi(s)$,为了实现这一个目标,有两种算法:value iteration和policy iteration,需要注意的是这两种算法都是计划算法(Planning Algorithms),和我们真正意义上的学习、RL还是有差距的。
value iteration
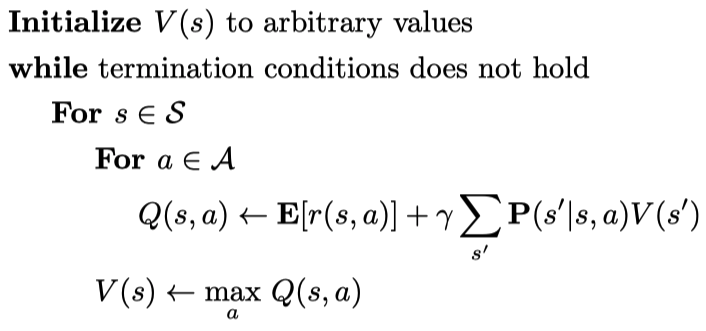
Policy Iteration
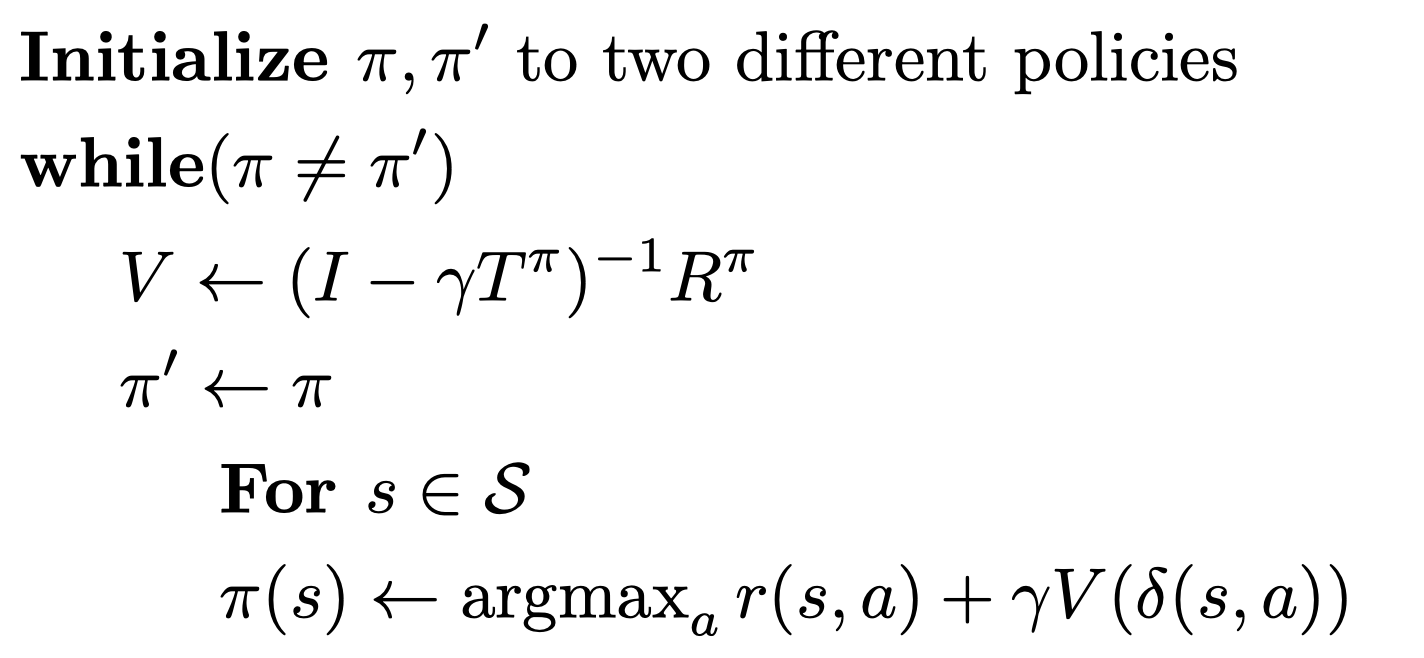
我们可以证明,这两种算法都能够通过迭代收敛到最优的$V$值。也就是说,我们通过这两种算法,不断的改进我们的policy即$pi$,使得每个状态下的$V(s)$逐渐增大,最终收敛到$V^*(s)$。注意这里每个状态的价值都是非减的,这是马尔科夫性决定的,我们的政策始终在不断的、贪心的进行着优化,最终,Value迭代得到了最优的Value值(还需要简单的一步转化才能得到最优的政策),Policy迭代则直接得到了最优的政策$pi$。
我写了一段代码对上述过程进行说明,见https://www.cnblogs.com/chester-cs/p/13403879.html