转载请注明出处：https://www.cnblogs.com/chenzhihong294/p/11329669.html
先给出一个实例：
学生评判系统升级，现在评选一个学生是否优秀需要从学科成绩、科研成绩、竞赛成绩、体育素质......等n个角度来评测、每一个角度所占的评选标准比例又不一样。我们如何根据上一届优秀学生各方面成绩来设定各角度权比和优秀标准、完善评判系统，从而判断一个同学是否优秀呢？
我们可以将该问题转化为以下形式：
每个同学有n个评测角度(x)，每个评测角度有不同的标准占比(w)，当该学生得分超过某一门槛(threshold)时即可判定其为优秀，我们需要根据上一届优秀学生和非优秀学生的样本，找到最合理的w和threshold来构建评判系统。
首先数学化该问题：
如果该同学判定为优秀，则：
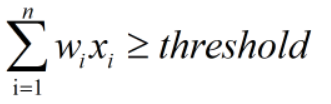
反之，若判定不优秀，则：
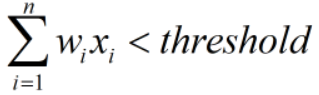
如果判定为优秀，我们将其value设为1，反之设为-1，则可以用到该函数：
故，我们可以将其改写为以下形式：
只需判断h(x)为 1 或者 -1 即可判定该同学是否优秀。
对此我们可以进一步化简，将：
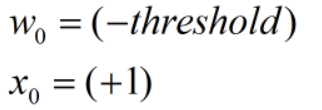
所以，函数可以写为：
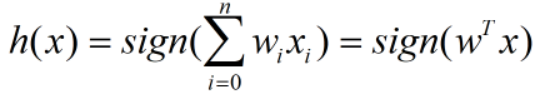
至此，问题数学化结束。
如何利用函数判定一位同学优秀与否：
对此，为了更加直观的面对该问题，我们假定只从两个角度来判定，即n=2，原式拆解后为：
可以看到函数
中，我们用x代替x1，用y代替x2，用c代替threshold后，它变成了：
更具体一点，如下所示，我们用图像来可视化它：
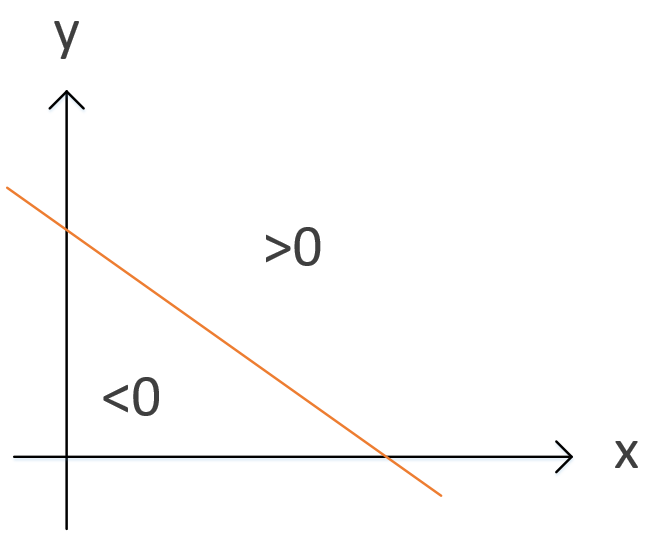
是的，它变成了二维平面上的一条直线，在直线上方的最终函数值为1，直线下方的最终函数值为-1。
原来判定一位同学是否优秀的问题变成了“怎么找到一条直线将优秀的同学和不优秀的同学分开”。
如何找到合适的w来完成模型构建：
设当前时刻为t，利用当前的h(x)遍历每一个样本 (xn(t),yn(t)) ，当发现错误时，即：
便修正w以尽量满足符合当前样本，具体修正方式如下：
为什么要这样修正呢，解释如下：
首先，向量点积有以下公式：
所以
因为前两项的值都为正，所以整个式子的正负情况只与两向量的夹角余弦值有关。
当y=+1，但两向量夹角大于90°，余弦值为负时，可以缩小两向量间的夹角大小，从而进行修正。
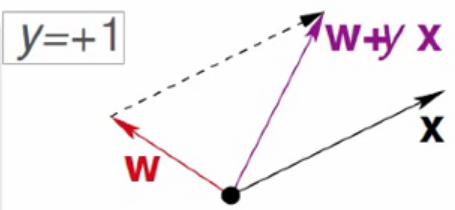
当y=-1，但两向量夹角小于90°，余弦值为正时，可以扩大两向量间的夹角大小，从而进行修正。
所以，经过不断地修正，可以得到一个完美的直线，区分优秀的同学和不优秀的同学。
如以下动图展示的过程，我们设蓝圈为优秀的同学，红叉为不优秀的同学，9次修成后，便得到了最优的分割线。
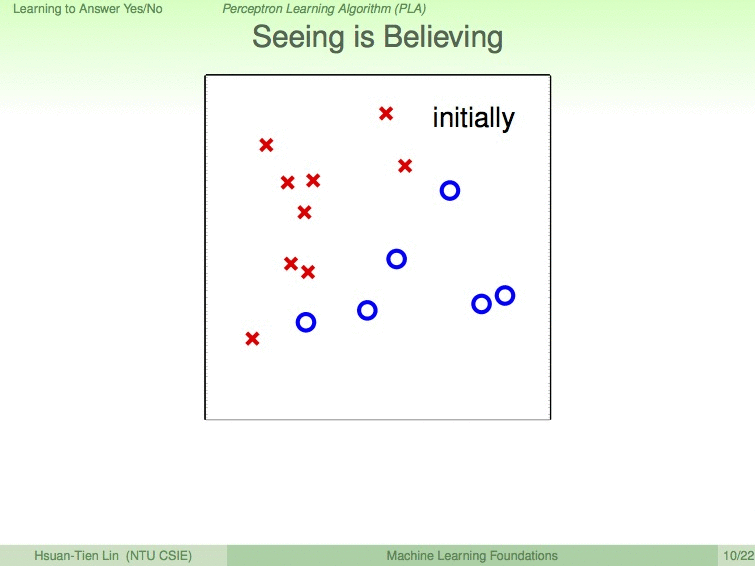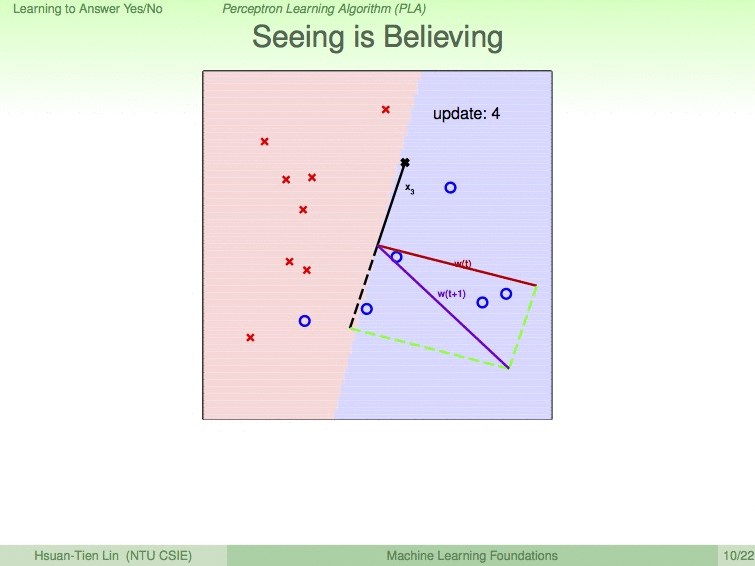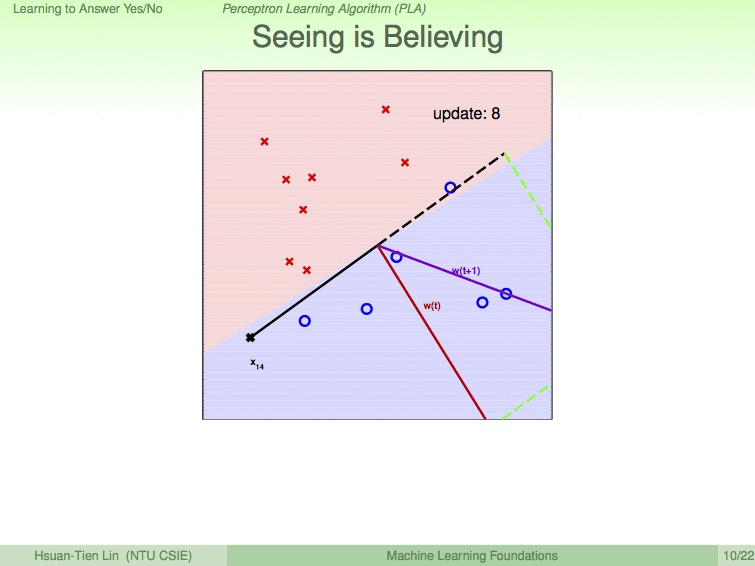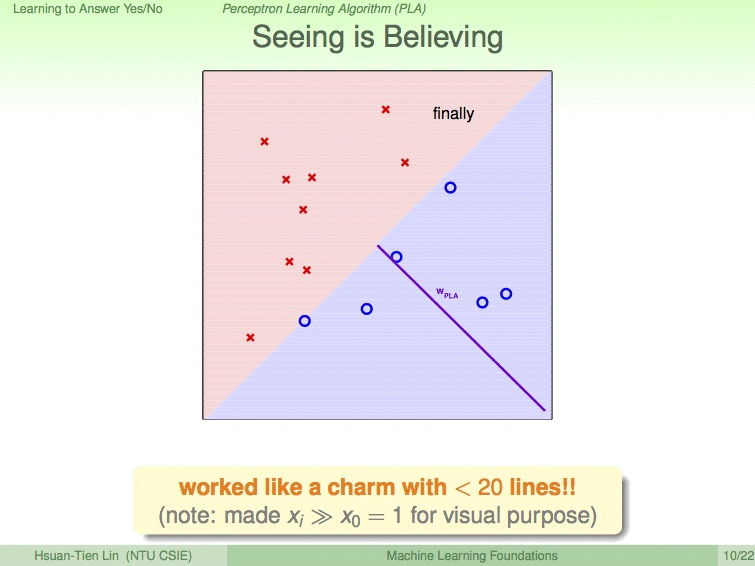
使用PLA需要注意的条件：
理论上该算法是构建一个n-1维的超平面在n维空间上进行二分类。
两组样本必须是线性可分的，不然算法永远找不到一个最优超平面，也代表它永远不会停止迭代，算法无解。
以上就是PLA的全部过程，小伙伴门有建议可以在下方评论。
如有需要，后续博主会根据情况补充PLA的其他形式或者其他解析方法。