有关树的理论部分描述:《数据结构与算法》-4-树与二叉树;
下面代码均基于python实现,包含:
- 二叉树的前序、中序、后序遍历的递归算法和非递归算法;
- 层次遍历;
- 由前序序列、中序序列重构二叉树;
- 由后序序列、中序序列重构二叉树;
# -*- coding: utf-8 -*-
# @Time: 2019-04-15 18:35
# @Author: chen
class NodeTree:
def __init__(self, root=None, lchild=None, rchild=None):
"""创建二叉树
Argument:
lchild: BinTree
左子树
rchild: BinTree
右子树
Return:
Tree
"""
self.root = root
self.lchild = lchild
self.rchild = rchild
class BinTree:
# -----------前序遍历 ------------
# 递归算法
def pre_order_recursive(self, T):
if T == None:
return
print(T.root, end=' ')
self.pre_order_recursive(T.lchild)
self.pre_order_recursive(T.rchild)
# 非递归算法
def pre_order_non_recursive(self, T):
"""借助栈实现前驱遍历
"""
if T == None:
return
stack = []
while T or len(stack) > 0:
if T:
stack.append(T)
print(T.root, end=' ')
T = T.lchild
else:
T = stack[-1]
stack.pop()
T = T.rchild
# -----------中序遍历 ------------
# 递归算法
def mid_order_recursive(self, T):
if T == None:
return
self.mid_order_recursive(T.lchild)
print(T.root, end=' ')
self.mid_order_recursive(T.rchild)
# 非递归算法
def mid_order_non_recursive(self, T):
"""借助栈实现中序遍历
"""
if T == None:
return
stack = []
while T or len(stack) > 0:
if T:
stack.append(T)
T = T.lchild
else:
T = stack.pop()
print(T.root, end=' ')
T = T.rchild
# -----------后序遍历 ------------
# 递归算法
def post_order_recursive(self, T):
if T == None:
return
self.post_order_recursive(T.lchild)
self.post_order_recursive(T.rchild)
print(T.root, end=' ')
# 非递归算法
def post_order_non_recursive(self, T):
"""借助两个栈实现后序遍历
"""
if T == None:
return
stack1 = []
stack2 = []
stack1.append(T)
while stack1:
node = stack1.pop()
if node.lchild:
stack1.append(node.lchild)
if node.rchild:
stack1.append(node.rchild)
stack2.append(node)
while stack2:
print(stack2.pop().root, end=' ')
return
# -----------层次遍历 ------------
def level_order(self, T):
"""借助队列(其实还是一个栈)实现层次遍历
"""
if T == None:
return
stack = []
stack.append(T)
while stack:
node = stack.pop(0) # 实现先进先出
print(node.root, end=' ')
if node.lchild:
stack.append(node.lchild)
if node.rchild:
stack.append(node.rchild)
# ----------- 前序遍历序列、中序遍历序列 —> 重构二叉树 ------------
def tree_by_pre_mid(self, pre, mid):
if len(pre) != len(mid) or len(pre) == 0 or len(mid) == 0:
return
T = NodeTree(pre[0])
index = mid.index(pre[0])
T.lchild = self.tree_by_pre_mid(pre[1:index+1], mid[:index])
T.rchild = self.tree_by_pre_mid(pre[index+1:], mid[index+1:])
return T
# ----------- 后序遍历序列、中序遍历序列 —> 重构二叉树 ------------
def tree_by_post_mid(self, post, mid):
if len(post) != len(mid) or len(post) == 0 or len(mid) == 0:
return
T = NodeTree(post[-1])
index = mid.index(post[-1])
T.lchild = self.tree_by_post_mid(post[:index], mid[:index])
T.rchild = self.tree_by_post_mid(post[index:-1], mid[index+1:])
return T
if __name__ == '__main__':
# ----------- 测试:前序、中序、后序、层次遍历 -----------
# 创建二叉树
nodeTree = NodeTree(1,
lchild=NodeTree(2,
lchild=NodeTree(4,
rchild=NodeTree(7))),
rchild=NodeTree(3,
lchild=NodeTree(5),
rchild=NodeTree(6)))
T = BinTree()
T.pre_order_recursive(nodeTree) # 前序遍历-递归
print('
')
T.pre_order_non_recursive(nodeTree) # 前序遍历-非递归
print('
')
T.mid_order_recursive(nodeTree) # 中序遍历-递归
print('
')
T.mid_order_non_recursive(nodeTree) # 前序遍历-非递归
print('
')
T.post_order_recursive(nodeTree) # 后序遍历-递归
print('
')
T.post_order_non_recursive(nodeTree) # 前序遍历-非递归
print('
')
T.level_order(nodeTree) # 层次遍历
print('
')
print('==========================================================================')
# ----------- 测试:由遍历序列构造二叉树 -----------
T = BinTree()
pre = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I']
mid = ['B', 'C', 'A', 'E', 'D', 'G', 'H', 'F', 'I']
post = ['C', 'B', 'E', 'H', 'G', 'I', 'F', 'D', 'A']
newT_pre_mid = T.tree_by_pre_mid(pre, mid) # 由前序序列、中序序列构造二叉树
T.post_order_recursive(newT_pre_mid) # 获取后序序列
print('
')
newT_post_mid = T.tree_by_post_mid(post, mid) # 由后序序列、中序序列构造二叉树
T.pre_order_recursive(newT_post_mid) # 获取前序序列
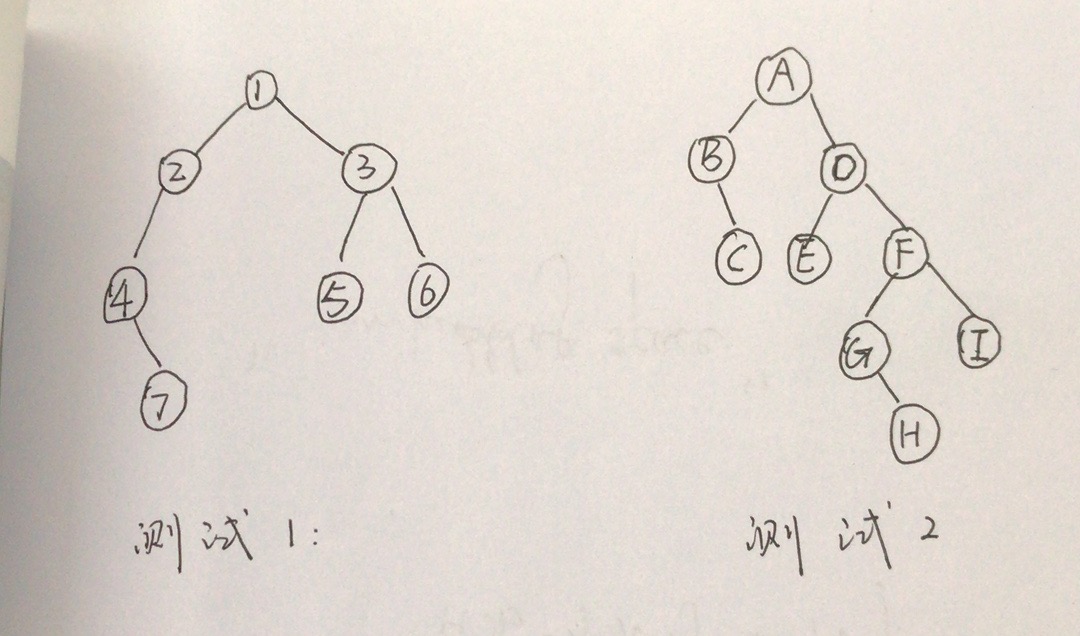
测试用的两个二叉树: