HDU-1254

推箱子

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 6048    Accepted Submission(s): 1729

Problem Description

推 箱子是一个很经典的游戏.今天我们来玩一个简单版本.在一个M*N的房间里有一个箱子和一个搬运工,搬运工的工作就是把箱子推到指定的位置,注意,搬运工 只能推箱子而不能拉箱子,因此如果箱子被推到一个角上(如图2)那么箱子就不能再被移动了,如果箱子被推到一面墙上,那么箱子只能沿着墙移动.

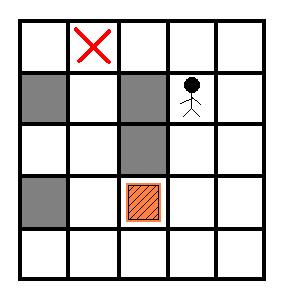
现在给定房间的结构,箱子的位置,搬运工的位置和箱子要被推去的位置,请你计算出搬运工至少要推动箱子多少格.

 

Input

输 入数据的第一行是一个整数T(1<=T<=20),代表测试数据的数量.然后是T组测试数据,每组测试数据的第一行是两个正整数M,N(2& lt;=M,N<=7),代表房间的大小,然后是一个M行N列的矩阵,代表房间的布局,其中0代表空的地板,1代表墙,2代表箱子的起始位置,3代 表箱子要被推去的位置,4代表搬运工的起始位置.

 

Output

对于每组测试数据,输出搬运工最少需要推动箱子多少格才能帮箱子推到指定位置,如果不能推到指定位置则输出-1.

 

Sample Input

1
5 5
0 3 0 0 0
1 0 1 4 0
0 0 1 0 0
1 0 2 0 0
0 0 0 0 0

 

Sample Output

4

 

Author

Ignatius.L & weigang Lee

/**
          题意：如题
          做法：bfs + dfs 
**/
#include <iostream>
#include <stdio.h>
#include <string.h>
#include <cmath>
#include <algorithm>
#include <queue>
#define maxn 10
#define INF 0x7fffffff
using namespace std;
int mmap[maxn][maxn];
int used[maxn][maxn];
int vis[maxn][maxn][maxn][maxn];
int n,m;
int dx[4] = {0,0,-1,1};
int dy[4] = {1,-1,0,0};
bool flag = false;
struct Node
{
    int bx;
    int by;
    int mx;
    int my;
    int step;
    Node() {}
    Node(int _bx,int _by,int _mx,int _my,int _step)
    {
        bx = _bx;
        by = _by;
        mx = _mx;
        my = _my;
        step = _step;
    }
};
int check(int x,int y)
{
    if(x >= 0 && x < n && y >= 0 && y <m && mmap[x][y] != 1) return 1;
    return 0;
}
void dfs(int bx,int by,int mx,int my)
{
    if(bx == mx && by == my)
    {
        flag = true;
        return ;
    }
    for(int i=0; i<4 && flag == false; i++)
    {
        int tx = bx + dx[i];
        int ty = by + dy[i];
        if(check(tx,ty)&&used[tx][ty] == 0)
        {
            used[tx][ty] = 1;
            dfs(tx,ty,mx,my);
        }
    }
}
void  bfs(int bx,int by,int mx,int my)
{
    queue<Node>que;
    while(!que.empty()) que.pop();
    Node tmp,now;
    tmp = Node(bx,by,mx,my,0);
    //cout<<tmp.bx<<"  "<<tmp.by<<"  "<<tmp.mx<<"  "<<tmp.my<<"   "<<tmp.step<<endl;
    que.push(tmp);
    while(!que.empty())
    {
        now = que.front();
        que.pop();
        if(mmap[now.bx][now.by] == 3)
        {
            printf("%d
",now.step);
            return;
        }
        for(int i=0; i<4; i++)
        {
            tmp.bx = now.bx + dx[i];
            tmp.by = now.by + dy[i];
            tmp.mx = now.bx - dx[i];
            tmp.my = now.by - dy[i];
            if(check(tmp.bx,tmp.by) && check(tmp.mx,tmp.my) && vis[tmp.bx][tmp.by][tmp.mx][tmp.my] == 0)
            {
                memset(used,0,sizeof(used));
                flag = false;
                used[now.bx][now.by] = 1;
                used[tmp.mx][tmp.my] = 1;
                dfs(tmp.mx,tmp.my,now.mx,now.my);
                if(flag == true)
                {
                    vis[tmp.bx][tmp.by][tmp.mx][tmp.my] = 1;
                    tmp.step = now.step + 1;
                    que.push(tmp);
                }
            }
        }
    }
    printf("-1
");
    return ;
}
int main()
{
//#ifndef ONLINE_JUDGE
//    freopen("in.txt","r",stdin);
//#endif // ONLINE_JUDGE
    int T;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d %d",&n,&m);
        int bx,by,mx, my;
        memset(vis,0,sizeof(vis));
        memset(mmap,0,sizeof(mmap));
        for(int i=0; i<n; i++)
        {
            for(int j=0; j<m; j++)
            {
                scanf("%d",&mmap[i][j]);
                if(mmap[i][j] == 2)
                {
                    bx = i;
                    by = j;
                }
                if(mmap[i][j] == 4)
                {
                    mx = i;
                    my = j;
                }
            }
        }
         bfs(bx,by,mx,my);
    }
    return 0;
}