前言
平衡树在我的心目中,一直都是一个很高深莫测的数据结构。不过,由于最近做的题目的题解中经常出现“平衡树”这三个字,我决定从最简单的替罪羊树开始,好好学习平衡树。
简介
替罪羊树,英文名\(Scapegoat\ Tree\),是我认为平衡树中最简单的一种。
替罪羊树可以当作一棵非常暴力的二叉搜索树,因为它除了在子树不平衡时会暴力重构(不然为什么叫它平衡树)以外几乎和BST没有任何区别。
替罪羊树的基础操作
-
插入
不得不说,替罪羊树的插入操作简直与BST一模一样。
直接上代码:
inline void Insert(int &x,int val)//插入操作
{
if(!x)//如果当前节点为空,那么就将元素插入这个节点
{
x=Void[tot--],node[x].Val=val,node[x].Exist=1,Build(x);
return;
}
++node[x].Size,++node[x].Fac;//将这个子树的大小加1
if(val<=node[x].Val) Insert(node[x].Son[0],val);//比较插入元素与当前元素,若小于等于当前元素,就插入到当前元素的左子树
else Insert(node[x].Son[1],val);//否则,就插入到当前元素的右子树
}
-
删除
替罪羊树的删除操作就很值得一提了。
在删除替罪羊树上的一个元素时,我们并不会将其暴力删除(虽然替罪羊树在重构时非常暴力,但它的暴力是有选择性的,
不然复杂度还不上天),而是标记这个节点不存在,并在计算它所在子树大小时将实际大小减1。这个思想是非常实用的,在许多地方我们都会用到。代码如下:
inline void Delete(int &x,int rk)//删除排名为rk的数
{
if(node[x].Exist&&!((node[node[x].Son[0]].Fac+1)^rk))//如果当前节点存在(没有被删除)且刚好排名为rk,我们就将其删除
{
node[x].Exist=0,--node[x].Fac;//标记其不存在,并将该子树的实际大小减1
return;
}
--node[x].Fac;//因为该子树中将有元素被删除,所以将该子树的实际大小减1
if(node[node[x].Son[0]].Fac+node[x].Exist>=rk) Delete(node[x].Son[0],rk);//比较删除元素与当前元素的大小,若小于等于当前元素,就说明要删除的元素在当前元素的左子树
else Delete(node[x].Son[1],rk-node[x].Exist-node[node[x].Son[0]].Fac);//否则说明要删除的元素在当前元素的右子树
}
inline void del(int v)//删除值为v的数
{
Delete(rt,get_rank(v));//删除值为v的数,就相当于删除排名为值为v的数的排名的数,是不是有点绕?
if((double)node[rt].Size*alpha>(double)node[rt].Fac) ReBuild(rt);//如果当前子树的实际大小小于该子树的大小乘以alpha(一般来说,取alpha=0.75),就重构该子树
}
-
重构
呃,接下来到了最关键的部分:重构。
替罪羊树的重构真的是非常暴力。我们可以形象地理解它:
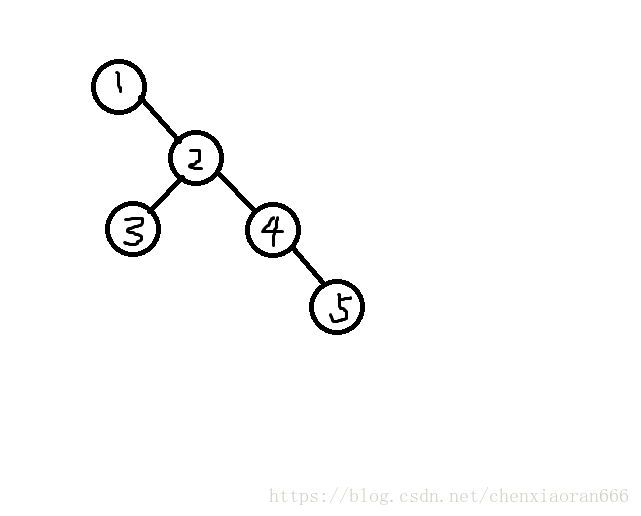
假设上图是一棵需要重构的子树(圆圈中是节点编号而不是节点权值)。
那么,我们就先非常暴力地将其拍扁:

然后,再将它以最中间的节点为新的根,重新拎起来:

重构就完成了。是不是一个极其暴力的过程?
代码如下:
inline void Traversal(int x)//拍扁原子树(中序遍历原子树,这样可以保证遍历后得到的元素是从大到小排序的)
{
if(!x) return;//如果当前节点是空节点,就退出函数
Traversal(node[x].Son[0]);//由于是中序遍历,所以先遍历该节点的左子树
if(node[x].Exist) cur[++cnt]=x;//如果该节点存在,就将其加入数组
else Void[++tot]=x;//否则删除该节点,将该节点加入存储空节点的数组,方便动态开点
Traversal(node[x].Son[1]);//最后遍历该节点的右子树
}
inline void SetUp(int l,int r,int &x)//将拍扁的树重新拎起(一个分治的操作)
{
int mid=l+r>>1;x=cur[mid];//将新的根节点设定为这段区间的中点(使重构出的树尽量平衡)
if(l==r)//如果这是一个叶子节点
{
Build(x);//重置该节点
return;//退出函数
}
if(l<mid) SetUp(l,mid-1,node[x].Son[0]);//如果当前元素左边还有数,说明它有左子树,重构它的左子树
else node[x].Son[0]=0;//否则它的左子树为空
SetUp(mid+1,r,node[x].Son[1]),PushUp(x);//重构它的右子树
}
inline void ReBuild(int &x)//重构的过程
{
cnt=0,Traversal(x);//拍扁
if(cnt) SetUp(1,cnt,x);//拎起
else x=0;//特判该子树为空的情况
}
-
询问
这应该是替罪羊树中最后一个比较基础的操作了。
作为一棵升级版的BST,它的功能与BST差不多:询问值为\(v\)的数的排名和排名为\(rk\)的数的值。
查询过程也与BST差不多,只不过要多判断一些节点不存在的情况。
代码如下:
inline int get_rank(int v)//询问值为v的数的排名
{
int x=rt,rk=1;//初始化计数器为1(v本身)
while(x)//只要当前节点不为空
{
if(node[x].Val>=v) x=node[x].Son[0];//如果当前元素大于v,则说明当前元素的排名大于v,所以访问当前元素的左子树
else rk+=node[node[x].Son[0]].Fac+node[x].Exist,x=node[x].Son[1];//否则,将计数器加上当前元素的排名,并访问当前元素的右子树
}
return rk;
}
inline int get_val(int rk)//询问排名为rk的数的值
{
int x=rt;
while(x)//只要当前节点不为空
{
if(node[x].Exist&&node[node[x].Son[0]].Fac+1==rk) return node[x].Val;//如果当前元素的排名等于rk,则返回该节点的值
else if(node[node[x].Son[0]].Fac>=rk) x=node[x].Son[0];//否则,如果当前元素的排名大于rk,访问当前元素的左子树
else rk-=node[x].Exist+node[node[x].Son[0]].Fac,x=node[x].Son[1];//不然,就将rk减去当前元素的排名,访问当前元素的右子树
}
}
完整代码
讲了这么多,最后来一个模板:(以【洛谷3369】【模板】普通平衡树为例)
#include<bits/stdc++.h>
#define N 100000
using namespace std;
int n,st,rt,cnt,tot,cur[N+5],Void[N+5];
const double alpha=0.75;
struct Scapegoat
{
int Son[2],Exist,Val,Size,Fac;
}node[N+5];
inline char tc()
{
static char ff[100000],*A=ff,*B=ff;
return A==B&&(B=(A=ff)+fread(ff,1,100000,stdin),A==B)?EOF:*A++;
}
inline void read(int &x)
{
x=0;int f=1;char ch;
while(!isdigit(ch=tc())) if(ch=='-') f=-1;
while(x=(x<<3)+(x<<1)+ch-'0',isdigit(ch=tc()));
x*=f;
}
inline void write(int x)
{
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10+'0');
}
inline void Init()
{
tot=0;
for(register int i=N-1;i;--i) Void[++tot]=i;
}
inline bool balance(int x)
{
return (double)node[x].Fac*alpha>(double)max(node[node[x].Son[0]].Fac,node[node[x].Son[1]].Fac);
}
inline void Build(int x)
{
node[x].Son[0]=node[x].Son[1]=0,node[x].Size=node[x].Fac=1;
}
inline void Insert(int &x,int val)
{
if(!x)
{
x=Void[tot--],node[x].Val=val,node[x].Exist=1,Build(x);
return;
}
++node[x].Size,++node[x].Fac;
if(val<=node[x].Val) Insert(node[x].Son[0],val);
else Insert(node[x].Son[1],val);
}
inline void PushUp(int x)
{
node[x].Size=node[node[x].Son[0]].Size+node[node[x].Son[1]].Size+1,node[x].Fac=node[node[x].Son[0]].Fac+node[node[x].Son[1]].Fac+1;
}
inline void Traversal(int x)
{
if(!x) return;
Traversal(node[x].Son[0]);
if(node[x].Exist) cur[++cnt]=x;
else Void[++tot]=x;
Traversal(node[x].Son[1]);
}
inline void SetUp(int l,int r,int &x)
{
int mid=l+r>>1;x=cur[mid];
if(l==r)
{
Build(x);
return;
}
if(l<mid) SetUp(l,mid-1,node[x].Son[0]);
else node[x].Son[0]=0;
SetUp(mid+1,r,node[x].Son[1]),PushUp(x);
}
inline void ReBuild(int &x)
{
cnt=0,Traversal(x);
if(cnt) SetUp(1,cnt,x);
else x=0;
}
inline void check(int x,int val)
{
int s=val<=node[x].Val?0:1;
while(node[x].Son[s])
{
if(!balance(node[x].Son[s]))
{
ReBuild(node[x].Son[s]);
return;
}
x=node[x].Son[s],s=val<=node[x].Val?0:1;
}
}
inline int get_rank(int v)
{
int x=rt,rk=1;
while(x)
{
if(node[x].Val>=v) x=node[x].Son[0];
else rk+=node[node[x].Son[0]].Fac+node[x].Exist,x=node[x].Son[1];
}
return rk;
}
inline int get_val(int rk)
{
int x=rt;
while(x)
{
if(node[x].Exist&&node[node[x].Son[0]].Fac+1==rk) return node[x].Val;
else if(node[node[x].Son[0]].Fac>=rk) x=node[x].Son[0];
else rk-=node[x].Exist+node[node[x].Son[0]].Fac,x=node[x].Son[1];
}
}
inline void Delete(int &x,int rk)
{
if(node[x].Exist&&!((node[node[x].Son[0]].Fac+1)^rk))
{
node[x].Exist=0,--node[x].Fac;
return;
}
--node[x].Fac;
if(node[node[x].Son[0]].Fac+node[x].Exist>=rk) Delete(node[x].Son[0],rk);
else Delete(node[x].Son[1],rk-node[x].Exist-node[node[x].Son[0]].Fac);
}
inline void del(int v)
{
Delete(rt,get_rank(v));
if((double)node[rt].Size*alpha>(double)node[rt].Fac) ReBuild(rt);
}
int main()
{
for(read(n),Init();n;--n)
{
int op,x;read(op),read(x);
switch(op)
{
case 1:st=rt,Insert(rt,x),check(st,x);break;
case 2:del(x);break;
case 3:write(get_rank(x)),putchar('\n');break;
case 4:write(get_val(x)),putchar('\n');break;
case 5:write(get_val(get_rank(x)-1)),putchar('\n');break;
case 6:write(get_val(get_rank(x+1))),putchar('\n');break;
}
}
return 0;
}