大致题意: 给你一个节点从(1sim n)编号的树,让你从中选择(k)个节点并通过选择的边联通,且要使选择的边数最少,让你计算对于所有选择(k)个节点的情况最小选择边数的总和。
题解
这道题乍一看很麻烦:最短路径?最小生成树?(LCA)?通通都不用!!!
其实,这道题就是一道很简单的数学题。
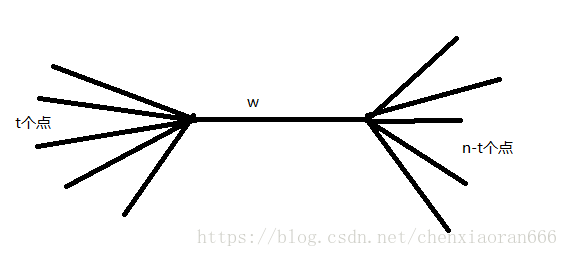
如上图所示,对于某一条边(w),假设它的一边共有(t)个节点,则显然它的另一边共有(n-t)个节点。
对于一条边的贡献,我们可以这样理解:在多少种情况下,这条边的两边都有被选入(k)个点中的点,此时这个点就必须被选。
而对于这些点的分布,有以下三种情况:
①这条边的两边都有点被选,这种情况的可能性就是我们要求的,但是难以直接计算。
②所有被选中的点都在这条边的左面,由于这条边的左边共有(t)个点,因此这种情况的可能性为(C_t^k)。
③所有被选中的点都在这条边的右面,由于这条边的右边共有(n-t)个点,因此这种情况的可能性为(C_{n-t}^k)。
由于总情况数为(C_n^k),所以,这条边的两边都有点被选的可能性就是(C_n^k) - (C_t^k) - (C_{n-t}^k)。
既然这样,我们可以直接枚举每一条边,计算出答案并累加即可。
代码
#include<bits/stdc++.h>
#define LL long long
#define N 100000
#define MOD 1000000007
using namespace std;
int n,k,ee=0,lnk[N+5],vis[N+5]={0};
struct edge
{
int to,nxt,val;
}e[2*N+5];
LL ans=0,fac[N+5]={0},inv[N+5]={0};
inline char tc()
{
static char ff[100000],*A=ff,*B=ff;
return A==B&&(B=(A=ff)+fread(ff,1,100000,stdin),A==B)?EOF:*A++;
}
inline void read(int &x)
{
x=0;int f=1;char ch;
while(!isdigit(ch=tc())) if(ch=='-') f=-1;
while(x=(x<<3)+(x<<1)+ch-'0',isdigit(ch=tc()));
x*=f;
}
inline void write(int x)
{
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10+'0');
}
inline void add(int x,int y)
{
e[++ee]=(edge){y,lnk[x],0},lnk[x]=ee;
}
inline LL quick_pow(LL x,LL y)//快速幂
{
LL res=1;
while(y)
{
if(y&1) (res*=x)%=MOD;
(x*=x)%=MOD,y>>=1;
}
return res;
}
inline void Init()//初始化
{
register int i;fac[1]=1;
for(i=2;i<=N+4;++i) fac[i]=(fac[i-1]*i)%MOD;//预处理阶乘
inv[N+4]=quick_pow(fac[N+4],MOD-2);
for(i=N+3;i>=0;--i) inv[i]=(inv[i+1]*(i+1))%MOD;//预处理逆元
}
inline LL C(LL x,LL y)//组合数
{
if(x<y) return 0;
if(!y) return 1;
return fac[x]*inv[y]%MOD*inv[x-y]%MOD;
}
inline int dfs(int x)
{
register int i;LL res=1;vis[x]=1;
for(i=lnk[x];i;i=e[i].nxt)
{
if(!vis[e[i].to])
{
LL t=dfs(e[i].to);
(ans+=C(n,k)%MOD-C(t,k)%MOD-C(n-t,k)%MOD+MOD)%=MOD;//核心计算公式
res+=t;
}
}
return res;//res表示该边某一侧的点数
}
int main()
{
register int i;int x,y;
for(read(n),read(k),i=1;i<n;++i)
read(x),read(y),add(x,y),add(y,x);
Init(),dfs(1);
return write((ans+MOD)%MOD),0;
}