1.学习总结(2分)
1.1图的思维导图
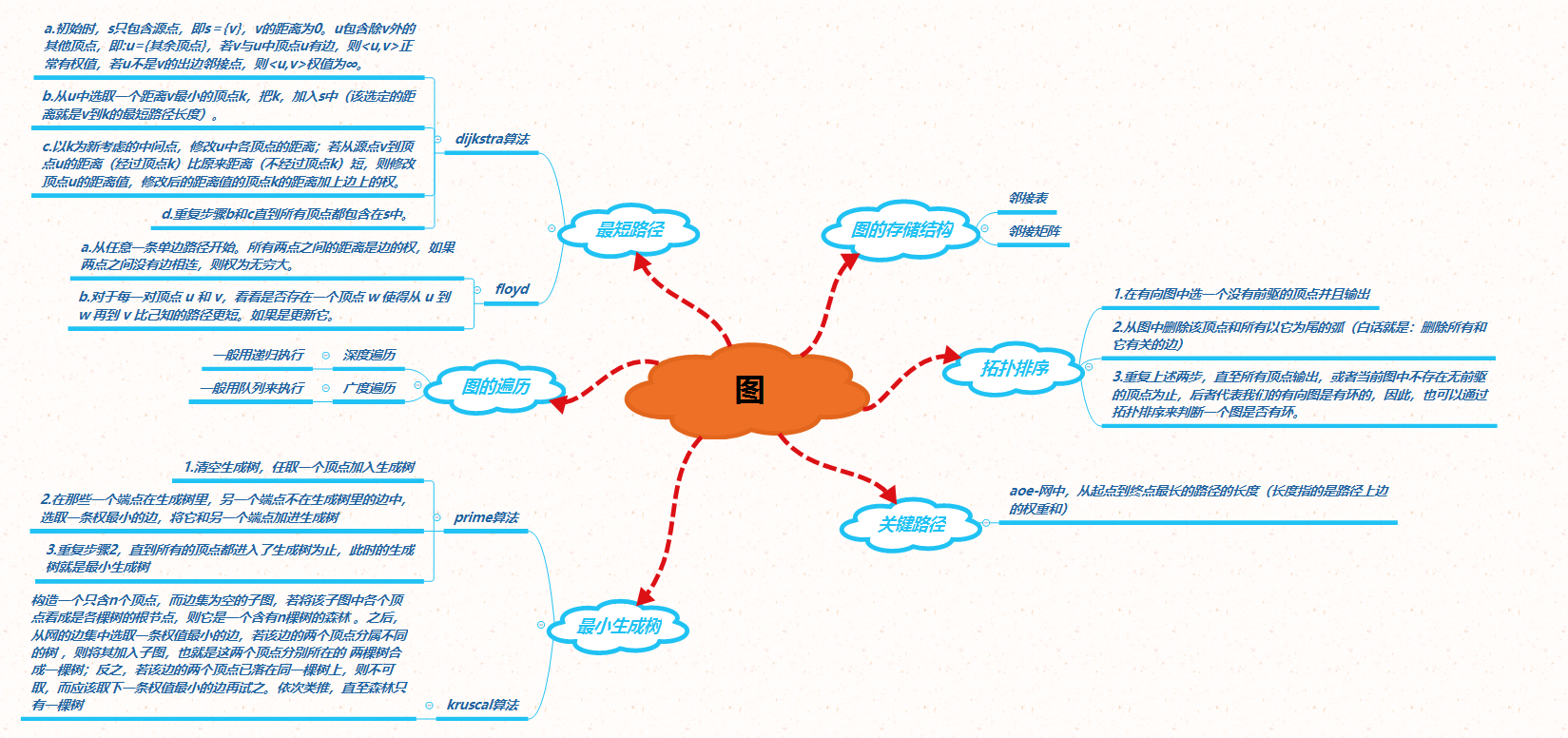
1.2 图结构学习体会
谈谈你对图结构中的几个经典算法学习体会。具体有:
深度遍历算法
类似于树的深度遍历,主要是利用递归来完成
广度遍历算法
类似于树的层次遍历,利用队列来完成
Prim和Kruscal算法
Prim算法是直接查找,多次寻找邻边的权重最小值,而Kruskal是需要先对权重排序后查找的。
Dijkstra算法
Dijkstra是一种贪心算法,用了广度优先搜索解决赋权有向图或者无向图的单源最短路径问题,最终得到一个最短路径树
拓扑排序算法
2.PTA实验作业(4分)
本周要求挑选出3道题目书写设计思路、调试过程。设计思路使用伪代码描述。题目选做要求:
不能选6-1,6-2,6-3
具体书写内容及格式如下:
2.1 题目1:7-1 图着色问题
2.2 设计思路
定义数组color[i] 代表第i个顶点的颜色
先判断方案中的颜色是否大于给定的颜色:
定义count[MAXV] 数组并且赋值 0
for i = 1 to n
count[color[i]] ++
若count[color[i]] == 1即该颜色第一次出现
num --(num为颜色总数)
end for
若num不等于0
出NO;
否则判断该方案的相邻顶点是否具有同一颜色:
for i = 1 to n
p = g -> adjlist[i].firstrac
while(p)
若color[i] == color[p -> adjvex]
表示相邻的颜色相同
输出 NO 并结束该函数
p = p -> nextarc;
end for
循环结束后表示该方案可行,输出yes
2.3 代码截图(注意,截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染)
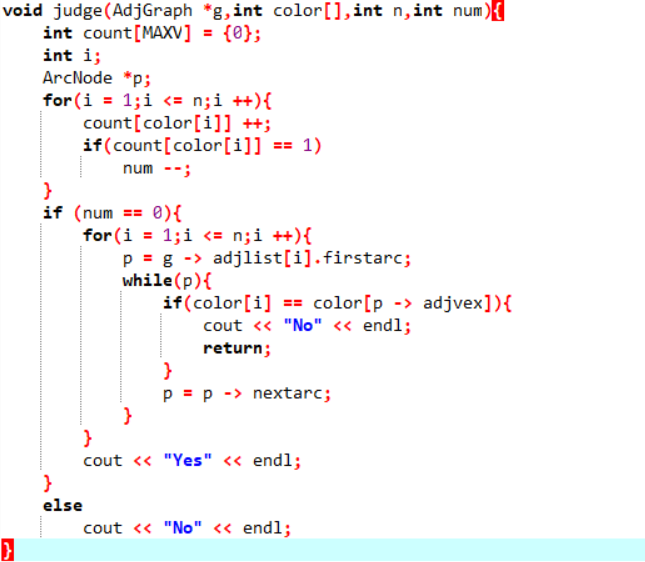
2.4 PTA提交列表说明。


最大图出现错误是因为数组不够大,修改MAXV即可。
2.5 题目2:7-2 排座位
2.6 设计思路
int edges[MAXV][MAXV];
int n,m; //图结构
int flag 用于 判断是否有共同朋友
int visited[]数组用于标记被访问过的顶点
该函数用于判断b1 b2是否有共同朋友
void find(int b1,int b2)
若b1 = b2
flag = true表示有共同朋友
用visited标记该顶点
for i = 1 to n
若 b1 与 i间有相连且i未被访问
访问find(i,b2)
end for
该函数判断能否同席
void judge()
for j = 1 to n
visited[j] = 0 初始化visited
flag = false 初始化flag
输入b1 b2
若edges[b1][b2] == 1
表示b1 b2 为好友
若edges[b1][b2] == 0
表示b1 b2无直接关系,需判断是否有共同朋友
find(b1,b2)判断是否有共同好友
若flag = true表示有
若flag = false表示无
edges[b1][b2] == -1
表示b1 b2为敌人,需判断是否有共同朋友
find(b1,b2)判断是否有共同好友
若flag = true表示有
若flag = false表示无
2.7 代码截图

2.8 PTA提交列表说明。
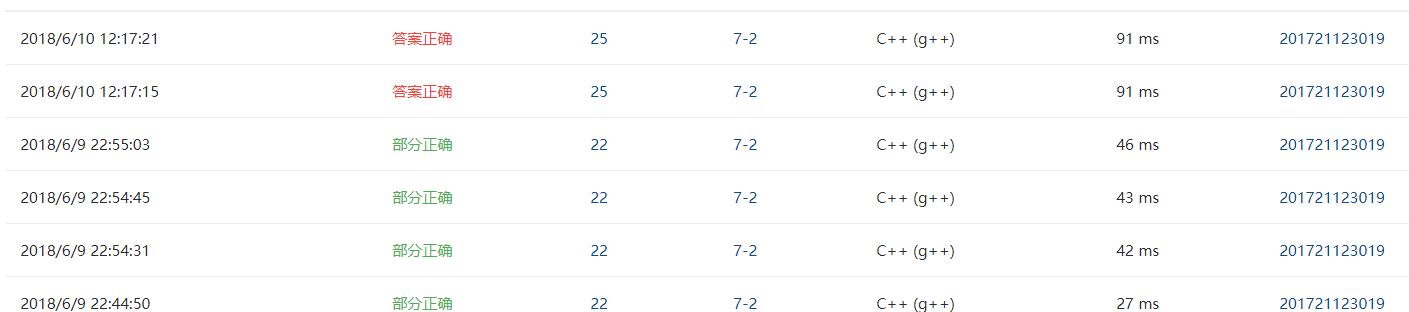

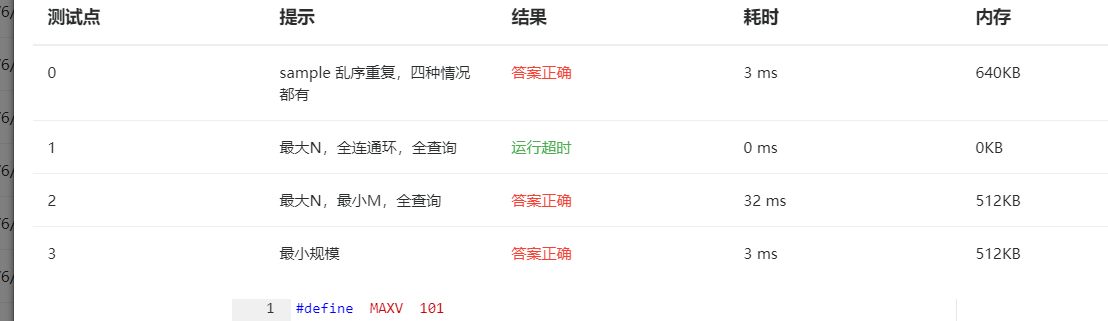
测试点1 运行超时,用了许多方法,后来定义如下的二维数组代替图结构,得以解决
2.9 题目3:7-4 公路村村通
2.10 设计思路
本题运用prime算法解决
int edges[MAXV][MAXV];
int n,e; //图结构
void prime()
定义lowcost[MAXV]数组表示某个顶点当前最低花费,并在确定该顶点的closest后将其赋值为0
定义closest[MAXV]数组表示某顶点最低花费情况下的前一个顶点
定义min存储最小值
for i = 1 to n
lowcost[i] = edges[1][i];
closest[i] = 1; 初始化最低花费和最近顶点
end for
for i = 1 to n
min = INF (INF为无限大,其值自定义一个较大的数)
for j = 1 to n
若 lowcost[j] != 0&&lowcost[j] < min
min = lowcost[j]
k = j
end for
end for
令k = j即令k 等于 离i最近的那个顶点
lowcost[k] = 0表示该顶点已被访问
for j = 1 to n 加入k后寻找新的最低花费
if(edges[k][j] != 0&&edges[k][j] < lowcost[j])
lowcost[j] = edges[k][j];
closest[j] = k
end for;
for i = 0 to n
累加各个最低花费并且输出
若出现某个顶点的最低距离为INF,表示无法畅通输出 -1
2.11 代码截图
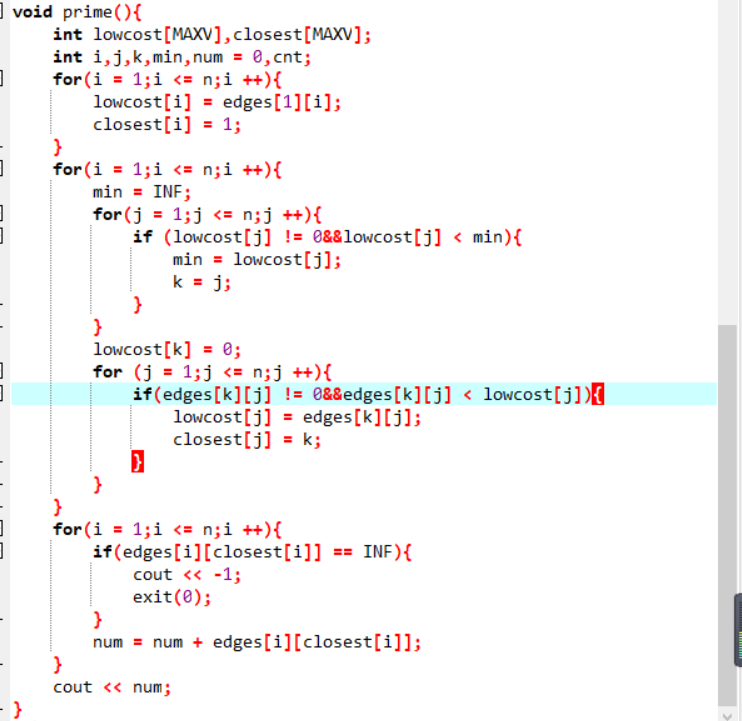
2.12 PTA提交列表说明
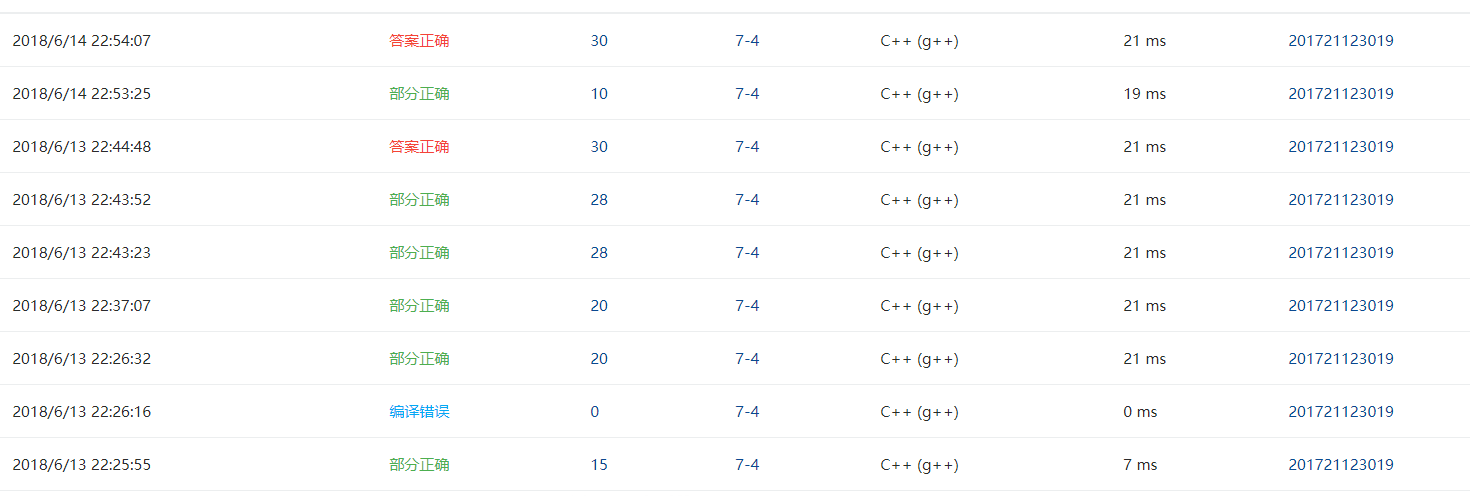

测试点1 添加判断条件后得以解决
测试点2 通过判断是否某个顶点的最低距离为INF,从而输出-1来解决
测试点4 同上
3.截图本周题目集的PTA最后排名

3.1 PTA排名(截图带自己名字的排名)
3.2 我的总分:2
4. 阅读代码(必做,1分)
旅游规划
#include<iostream>
#define INF 501
using namespace std;
bool visited[501]={false};
int vdist[501],vcost[501];
int dist[501][501],cost[501][501];
void dijstra(int s,int d,int n){
vdist[s]=0;visited[s]=true;
for(int i=0;i<n;i++){ //剩余n-1个节点 ,所以n-1次循环
//找出未被访问且距离最短的点
int mindist=INF;
int minvertex;
for(int j=0;j<n;j++){
if(!visited[j] && vdist[j]<mindist){
mindist=vdist[j];
minvertex=j;
}
}
//标记为访问过
visited[minvertex]=true;
//更新周围节点
for(int j=0;j<n;j++){
if(!visited[j] && vdist[minvertex]+dist[minvertex][j]<vdist[j]){
vdist[j]=vdist[minvertex]+dist[minvertex][j];
vcost[j]=vcost[minvertex]+cost[minvertex][j];
}else if(!visited[j] && vdist[minvertex]+dist[minvertex][j]==vdist[j] && vcost[minvertex]+cost[minvertex][j]<vcost[j]){
vcost[j]=vcost[minvertex]+cost[minvertex][j];
}
}
}
}
int main(){
//freopen("input.txt","r",stdin);
int v,e,s,d,v1,v2,curdist,curcost,i,j;
cin>>v>>e>>s>>d;
//1、初始化
for(i=0;i<v;i++){
for(j=0;j<v;j++){
dist[i][j]=dist[j][i]=INF;
cost[i][j]=cost[j][i]=INF;
}
}
//2、
for(i=0;i<e;i++){
cin>>v1>>v2>>curdist>>curcost;
dist[v1][v2]=dist[v2][v1]=curdist;
cost[v1][v2]=cost[v2][v1]=curcost;
}
//3、
for(i=0;i<v;i++){
vdist[i]=dist[i][s];
vcost[i]=cost[i][s];
}
//4、
dijstra(s,d,v);//s源点,d终点,v顶点数
cout<<vdist[d]<<" "<<vcost[d]<<endl;
return 0;
}
本题主要用了Dijkstra算法,用了2个二维数组来存储2个顶点间的距离和费用,vdist 和 vcost用于存储最短距离和花费,方便替换。
该代码在某些重要的地方进行了注释,并且注明了1 2 3 4,对缩进的的处理也很好