1、01背包是解决什么问题?
答:当书包容量大小固定,面对1堆重量固定而且带有价格的物品。在不超出包容量前提下,选择那些物品使包里物品总价值最大。
2、问:为什么01背包?
答:因为0表示不将物品放进包里,1表示将物品放进包里。
放:意味着包的容量减小,总价值增大。
不放:意味着包容量不变,总价值不变。
3、引入题目帮助分析
3.1、 题目:01背包问题描述:有编号分别为a,b,c,d,e的N=5件物品,它们的重量w分别是2,2,6,5,4,它们的价值v分别是6,3,5,4,6,每件物品数量只有一个,现在给你个承重为M=10的背包,如何让背包里装入的物品具有最大的价值总和sum_v?
3.2、上面题目反映到下面表格。下面表格1-10是容量,每格容量下面是最大价值。
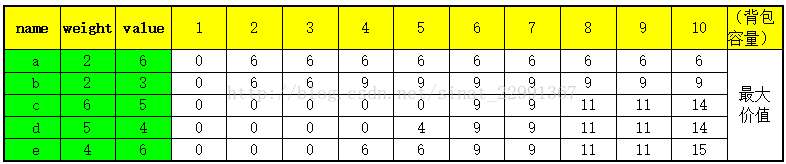
3.2、表格是怎样推算出来的?
第一步:将物品排列起来,从最大容积最后一个物品开始推算(即从下往上,从右往左)
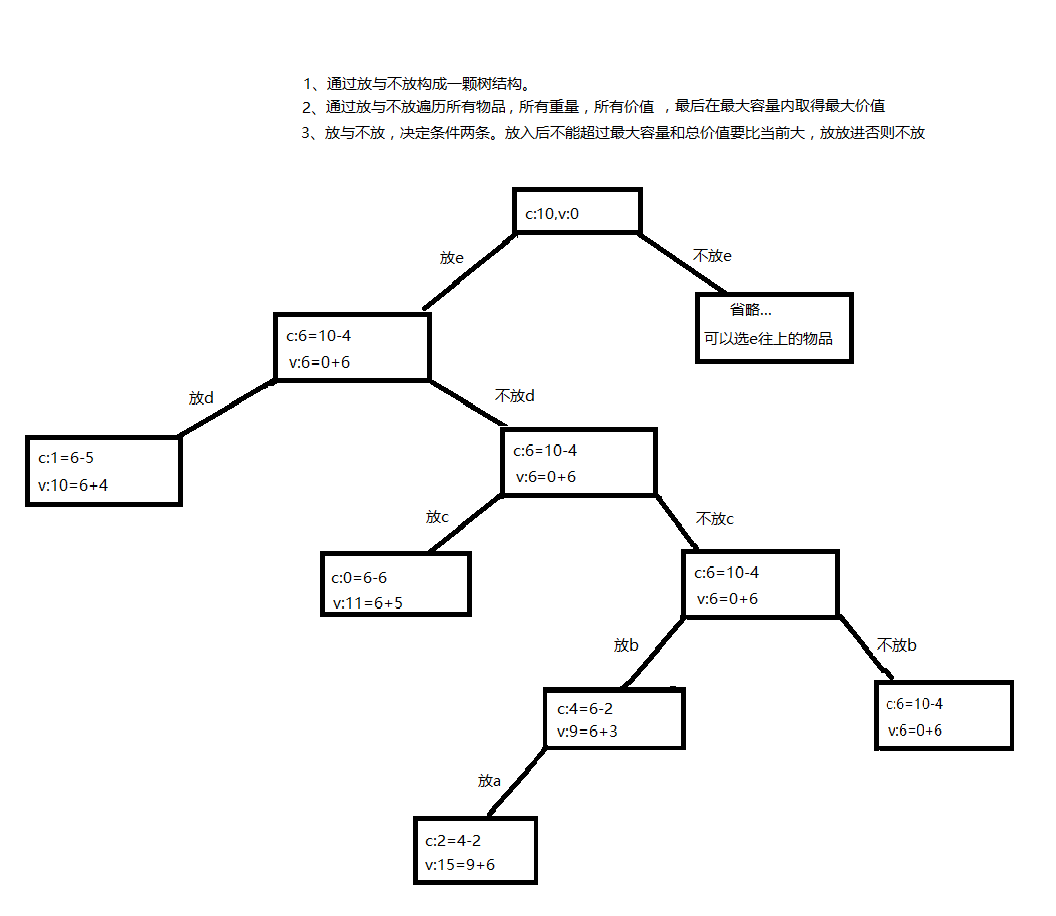
问:e(10) = 15 是什么意思? 背包容量10,从e物品开始往上取物品,能取到最大价值是15。那么15是怎样推算的?
答:下图推算最大价值15。1-10每个格子最大价值都是这样计算。这样把表都算好了,最大价值就一目了然。
四、通过代码实现
参考:https://jingyan.baidu.com/album/414eccf66d98dc6b421f0a6d.html?picindex=1
问题描述:给定n种物品和一背包。物品i的重量是w[i],其价值为v[i],背包的容量为C。问应如何选择装入背包的物品,使得装入背包中物品的总价值最大?
分析:对于一种物品,要么装入背包,要么不装。所以对于一种物品的装入状态可以取0和1。设物品i的装入状态为xi,xi∈ (0,1),此问题称为0-1背包问题。
数据:物品个数n=5,物品重量w[5]={2,2,6,5,4},物品价值v[5]={6,3,5,4,6},总重量c=10。背包的最大容量为10,那么在设置数组m大小时,可以设行列值为5和10,那么,对于m(i,j)就表示可选物品为i到n且背包容量为j(总重量)时背包中所放物品的最大价值。看下面这个表格即为动态规划法解0-1背包问题的过程:
public class KnapsackDemo { public static void main(String []args) { System.out.println("KnapsackDemo!!!"); int[] w = {2,2,6,5,4}; int[] v = {6,3,5,4,6}; int c = 10; int[][] m; int[] x; m = KnapsackDemo.knapsack(w,v,c); x = KnapsackDemo.buileSolution(m,w,c); for(int i=0;i<4;i++){ System.out.print(x[i]+" "); } } //0-1背包问题的算法 public static int[][] knapsack(int[] w,int v,int c){ int i,j,n = w.length int[][] m = new int[n+1][c+1]; for(i=1;i<n+1;i++){ m[i][0]=0; } for(j=0;j<c+1;j++){ m[0][j]=0; } int count=0; for(i=1;i<=n;i++){ for(j=1;j<=c;j++){ m[i][j] = m[i-1][j]; if(w[i-1]<=j){ if(v[i-1]+m[i-1][j-w[i-1]]>m[i-1][j]){ m[i][j]=v[i-1]+m[i-1][j-w[i-1]]; } } count++; } } System.out.println(count); return m } //依据m[][]实现对符合结果要求的物品进行选择的构建一个数组存储选择的情况0否1选择 public static int[] buileSolution(int[][] m,int[] w,int c){ int i,j = c,n = w.length; int[] x = new int[n]; for(i=n;i>=1;i--){ if(m[i][j]==m[i-1][j]){ x[i-1] = 0; }else{ x[i-1]=1; j -= w[i-1]; } } return x; } }